Indices (law of exponents)
Three basic rules including the Indices are:
i) am x an = am + n
ii) am ÷ an = am – n
iii) (am) n = am
Negative indices
Consider a5 ÷ a2 = a5
– 2 = a3
= a2 ÷ a5 = a2
– 5 = a -3


 In general
In general
 a -m =
a -m = 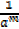
Fractional indices
Consider 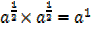
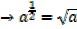
Similarly

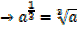
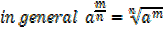
Zero exponents
Consider am x ao = am + o
 ao = 1
ao = 1
Laws of logarithm
If a and b are two positive numbers there exist a third number c such that
ac = b
→c is the logarithm of b to base a
i. e 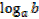 = c
= c
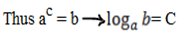
Definition
Logarithm of ‘x’ to base ‘a’ is the power to which ‘a’ must be raised to give ‘x’.
If p = 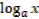 and q =
and q =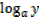 , then
, then  = x and
= x and 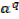 = y
= y
Thus
1. 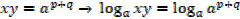
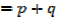
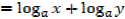
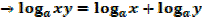
2. 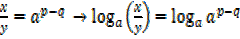
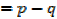
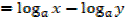
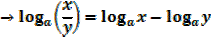
3. 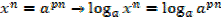

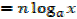
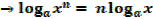
Change of base
If y = 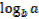
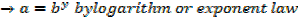
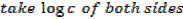
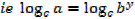
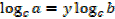
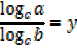
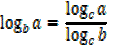
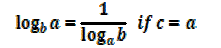
EXAMPLE
1. Solve for x, 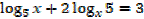
Solution
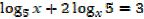
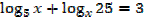
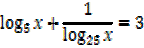
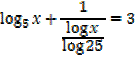
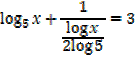
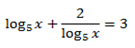
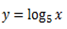
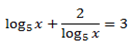
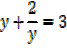
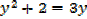

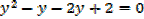

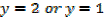
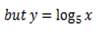

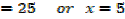
Note that:
There are two important bases of logarithms
10 and e
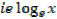
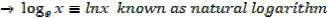
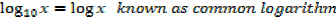
Series
A series is the sum of a sequentially ordered finite or infinite set of terms
Finite series
– Is the one have defined first and last term e.g. 1 + 3 + 5 + 7 + 9 + 11…… + 21 is a finite series
Infinite series
– Is the one have defined the first but not the last term e.g. 1 + 3+ 5+ 7+ 9+ 11+ …..
In both cases the first term is 1
The sigma notation
∑ stands for ” sum of ”
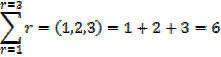
e.g.
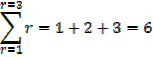
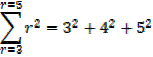
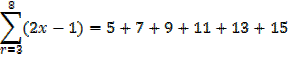
Exercise
Discuss the following and find the sum if n = 8

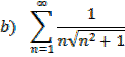
The sum of the first n natural numbers

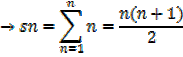
The sum of squares of the first n natural numbers
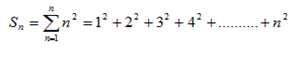
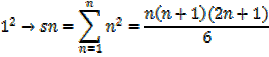
The sum of the cubes of the first n natural numbers
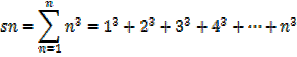


Example
I. If an = n2 + 3n + 1 determine an expression for n
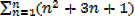
II. If an = n3 + 2n2 + 4n evaluate
a) a1 b) a4 c)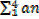
The sum of the first n natural numbers
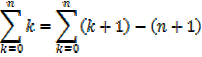
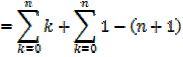

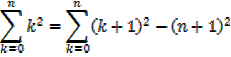
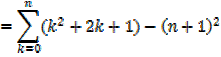
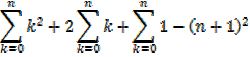
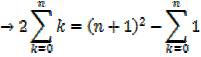
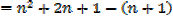
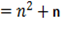
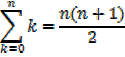
The sum of the squares of the first n natural numbers

Proof,
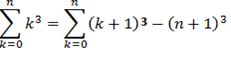
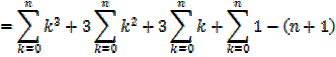


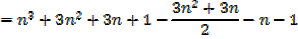
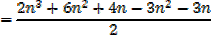
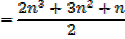
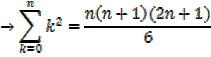
Exercise
1. Evaluate 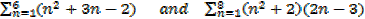
Proof by the mathematical induction
Example
Prove that n (n2 + 5) is exactly divisible by 3 for all positive integers n
Proof: I
Let n = 1; 1(12 + 5) = 6 = 3 x 2
n = 2; 2 (22 + 5) = 18 = 3 x 6
n = 3; 3 (32 + 5) = 42 = 3 x 14
n = 4; 4 (42 + 5) = 84 = 3 x 28
n = 7; 7 (72 + 5) = 378 = 3 x 126
Proof: II
i) Let n = 1 = 1 (12 + 5) = 6 = 3 x 2
ii) Let n (n2 + 5) be divisible for n = k
i.e. k (k2 + 5) = 3p, where p is any integers
iii) When n = k + 1
(k + 1) ( (k +1)2 + 5) = (k + 1) (k2 + 2k + 1 + 5)
= (k + 1) ((k2 + 5) + (2k + 1))
= k (k2 + 5) + k (2k + 1) + (k2 + 5) + (2k +1)
= 3p + 2k2 + k + k2 + 5 + 2k +1
= 3p + 3k2 + 3k + 6
= 3 (p + k2 + k + 2)
Since p and k are positive integers
So the number in the bracket is positive
iv) Since when n = 1 the values 1 (12 + 5) is divisible by 3 then the value n (n2 + 5) will be divisible by 3 for n = 2, n = 3, n = 4…… by the above working
→n (n2 + 5) is divisible by 3 for all n∈
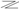 +
+
Principle of proof by mathematical induction
It states if s1, s2, s3…..Sn…. is a sequence of statements and if
i) s1 is true
ii) Sn → Sn + 1, n = 1, 2, 3 … are true, then s1, s2, s3…… Sn… are true statement
Examples
1. Prove by mathematical induction that 2 + 4+ 6 +…..2n = n (n + 1)
Solution
When n = 1
L. H. S = 2, R. H. S = 1(1 + 1) = 2
L. H.S = R. H. S
It is true for n = 1
Let the statement be true for n = k
2 + 4 + 6 + …. 2k = k (k + 1)
Required to prove when n = k + 1
2 + 4 + 6 + …… 2k + 2(k + 1) = k (k + 1) + 2(k + 1)
= k2 + k + 2k + 2
= k2 + 3k + 2
= k2 + k + 2k + 2
= k (k + 1) + 2 (k + 1)
= (k + 1) (k + 2)
Which is the same as putting n = k + 1 in the formula
Since n = 1gave a true statement, n =2, n = 3, n = 4… will be true statement as worked above
2. 2. Prove by induction that 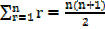
Solution
Proof:
When n = 1, 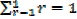
Also n = 1 give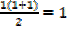
L.H.S = R. H. S
Let the statement be true for n =k
Let 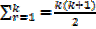
Required to prove when n = k + 1
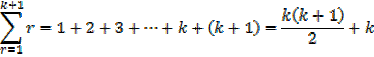
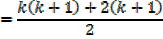
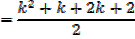
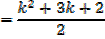
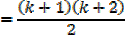
Which is the same as putting n = k + 1 in the form
Since n = 1 gave a true statement
n = 2, n = 3, n = 4… will give true statement
3. Prove that 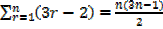
Solution
Proof:
When n = 1
L.H. S = 3 x 1 – 2 = 1
R.H.S = 
L.H.S = R.H.S
Let the statement be true for n = k
I.e. 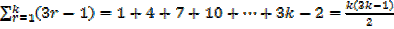 required to prove when n = k + 1
required to prove when n = k + 1
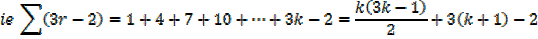
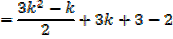
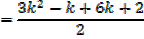
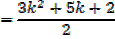
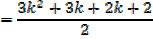

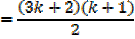
Which is the same as putting n = k + 1 in the formula since n = 1 gave a true statement,
n =2, n = 3, n = 4 … will give true statement