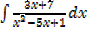ADVANCED MATHEMATICS FORM 5 – INTEGRATION

Integration :Is the reverse process of differentiation, i.e. the process of finding the expression for y in terms of x when given the gradient function.

The symbol for integration is, denote the integrate of a function with respect to x

If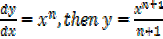

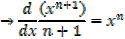
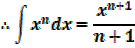
This is the general power of integration it works for all values of n except for n = -1

Example

1.     

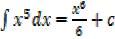
2.       Integrate the following with respect to x
(i)3x²

Solution

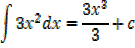
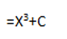
            Integration of constant

The result for differentiating c x is c

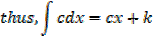
            Properties

(1) 

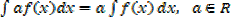
(2) 

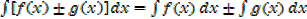
Integration by change of variables

If x is replaced by a linear function of x, say of the form ax + b, integration by change of variables will be applied
E.g.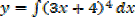    

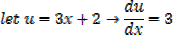
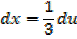
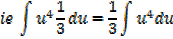
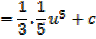
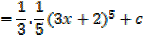
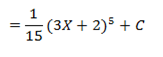
Considering 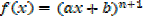in similar way gives the general result

         

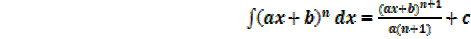
Example

Find the integral of the following

            a) (3x – 8) ⁶              b)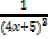

Solution (a)

 

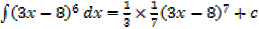
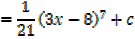
Solution (b)

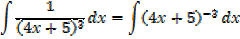
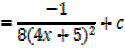
            → If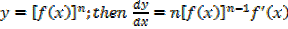

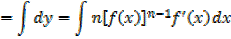
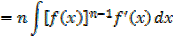
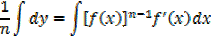
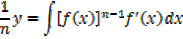
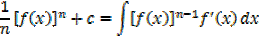
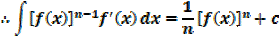
Example

1.   Find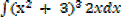 

            Solution

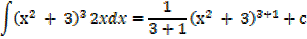
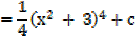
2.   Find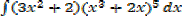

            Solution

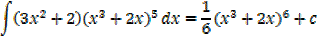
Integration of exponential function

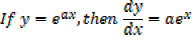
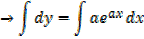
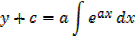
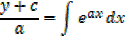
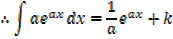
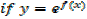
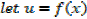
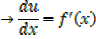
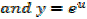
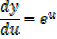
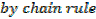
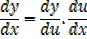
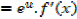
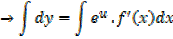
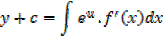
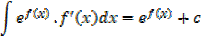
Example 01

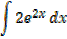
            Solution

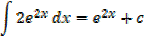
Alternative

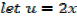
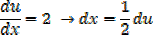
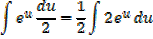
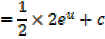
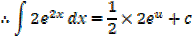
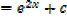
Example 02

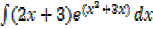
Solution

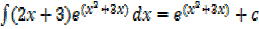
Alternative

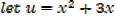
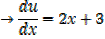
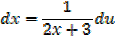
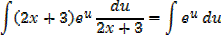
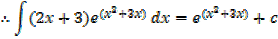
Integrating fraction

If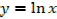 

Differentiating with respect to x gives

           

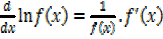
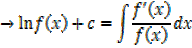
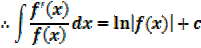
Example

1. 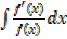  ,given that f(x)=x²+1

Solution

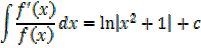
2.      Find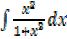

solution

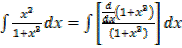
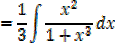
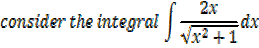
Note: 2x  is the derivative of x² + 1 in this case substitution is useful

           i.e. let u = x² + 1

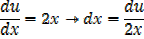
   This converts into the form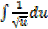    

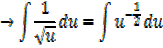
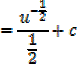
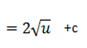
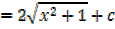
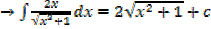
Standard integrals

·       

·       

·       

·       

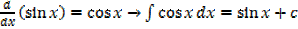
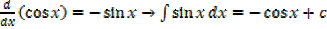
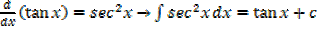
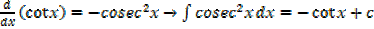
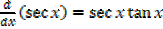·        →∫sec x tan xdx=sec x+c

·       

·       

·       

·       

·       

·       
·      

·       

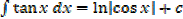
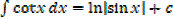
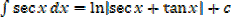
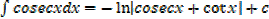
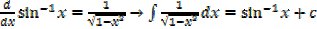
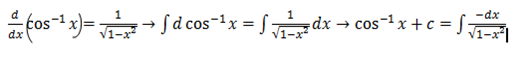
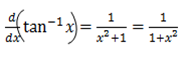
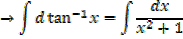
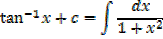
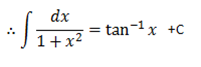
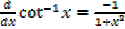
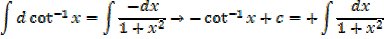
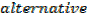
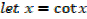
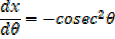
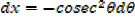
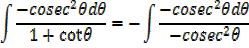
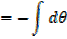
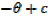
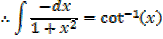
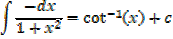
EXERCISE

Find the integral of the following functions

i)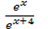  

ii)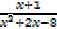  

iii)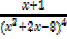 

iv)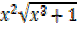 

Integration by partial fraction

Integration by partial fraction is applied only for proper fraction

E.g.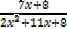 

Note that:

 The expression is not in standard integrals

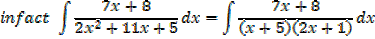
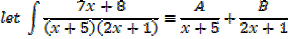
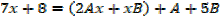
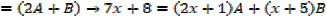
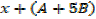
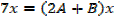
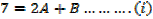
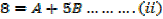
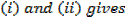
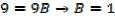
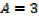
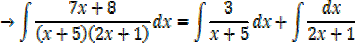
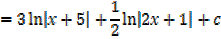
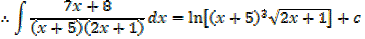
Example 01

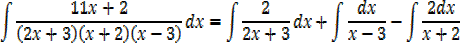
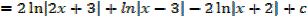
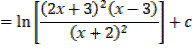
Example 02

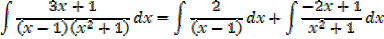
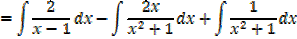
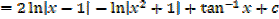
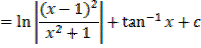
Improper fraction

If the degree of numerator is equal or greater than of denominator, adjustment must be made

Example

1.      Find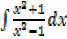 

Solution

 Both numerator and denominator have the degree of 2

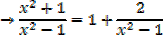
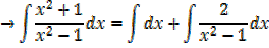
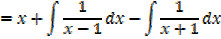
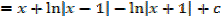
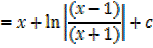
2.     

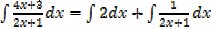
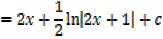
3.     

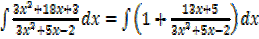
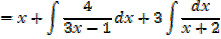
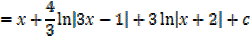
If the denominator doesn’t factorize, splitting the numerator will work

→ Numerator = A (derivative of denominator) + B

Example

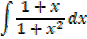
Solution

           
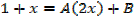
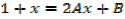
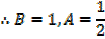
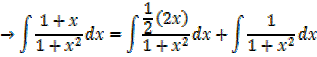
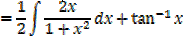
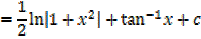
Important

It can be shown that

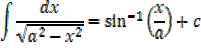
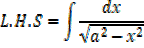
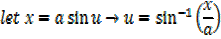
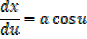
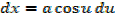
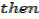
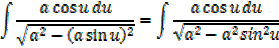
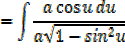
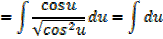
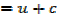
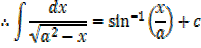
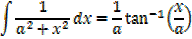
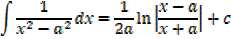
EXERCISE

                                I.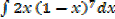           

                             II.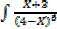           

                           III.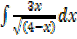           

Integrated of the form

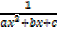
Note that:

1. If the denominator has two real roots use partial fraction

2. If the denominator has one repeated root use change of variable or recognition

3. If the denominator has no real roots, use completing the square

E.g.

                                I.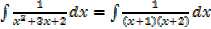           

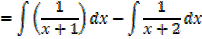
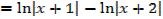
                             II.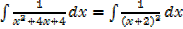     

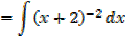
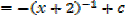
                           III.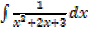    

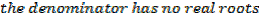
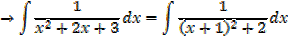
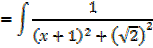
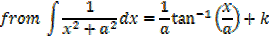
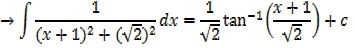
Integral of the form

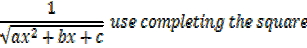
Example
→

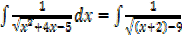
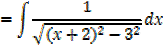
Then hyperbolic function identities is identities is used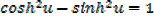

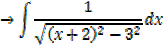
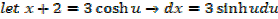
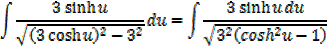
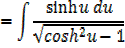
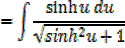
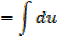
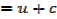
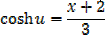
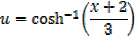
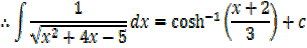
Note that:

If the quadratic has 1 represented root, it is easier

E.g.

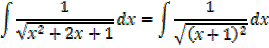
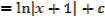
EXERCISE

Find the following

     i.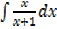     

     ii.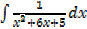   

     iii.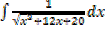  

     iv.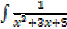  

     v.