ADVANCED MATHEMATICS FORM 6 – COORDINATE GEOMETRY II

CONIC SECTIONS

Definition

Conic sections or conics are the sections whose ratios of the distance of the variables point from the fixed point to the distance, or the variable point from the fixed line is constant

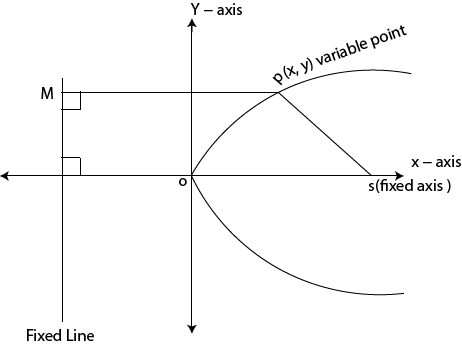
TYPES OF CONIC SECTION

There are     i) Parabola

ii) Ellipse

                   iii) Hyperbola

IMPORTANT TERMS USED IN CONIC SECTION

I.        FOCUS

This is the fixed point of the conic section.

For parabola

         

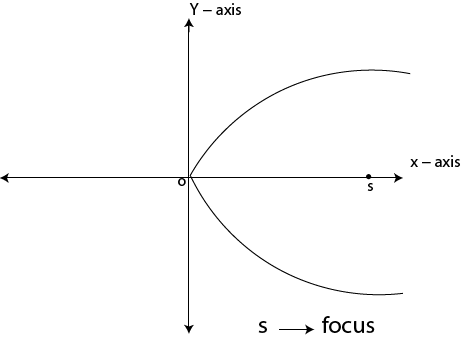
S → focus

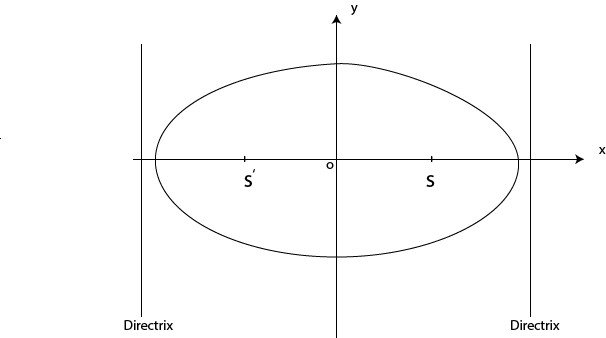
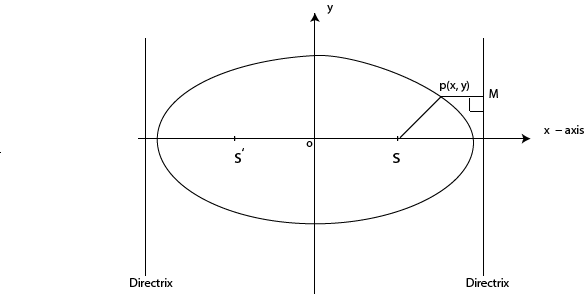
          For ellipse

         

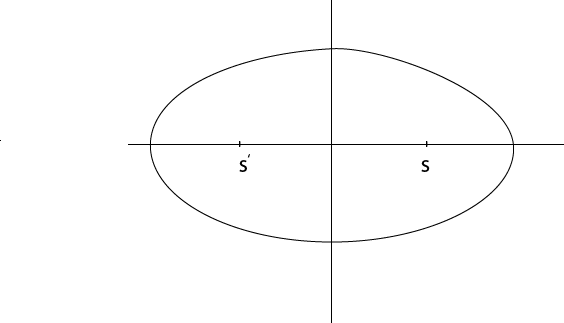
                                       S and S’ are the foci of an ellipse

II.  DIRECTRIX

This is the straight line whose distance from the focus is fixed.

For parabola

         

For ellipse

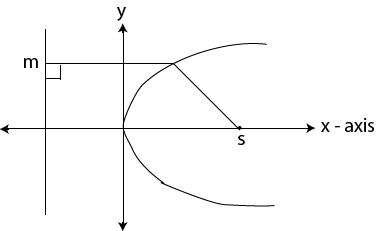
III.      ECCENTRICITY (e)

This is the amount ratio of the distance of the variable point from the focus to the distance of the variables point from the directrix.

For Parabola

     For ellipse

         

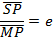
IV.   AXIS OF THE CONIC

This is the straight line which cuts the conic or conic section symmetrically into two equal parts.

For parabola

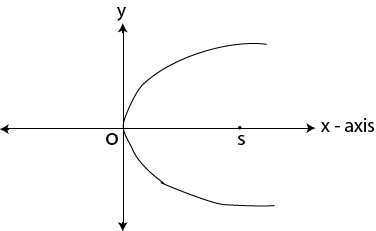
X-axis is the point of the conic i.e. parabola

Also

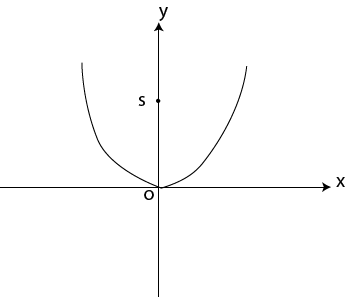
Y-axis is the axis of the conic

FOR ELLIPSE

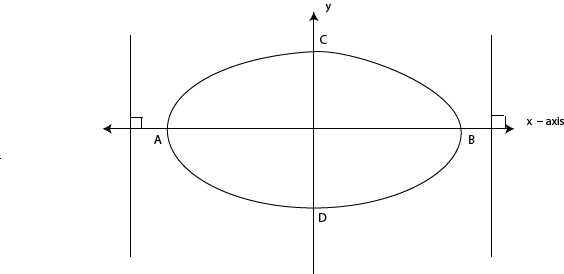
          AB – is the axis (major axis) of the Conic i.e. (ellipse)

CD – is the axis (minor axis) the Conic i.e. (ellipse)

→An ellipse has Two axes is major and minor axes

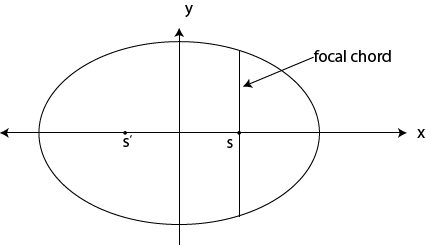
V    FOCAL CHORD

This is the chord passing through the focus of the conic section.

For parabola

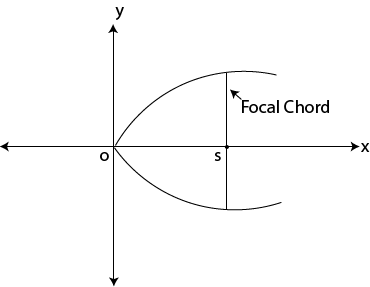
For ellipse

VI  LATUS RECTRUM

This is the focal cord which is perpendicular to the axis of the conic section.

For parabola

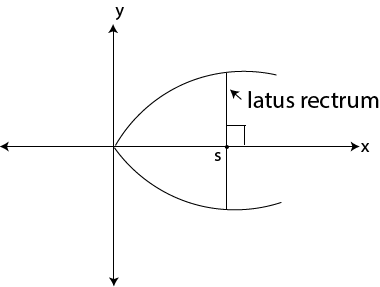
For Ellipse

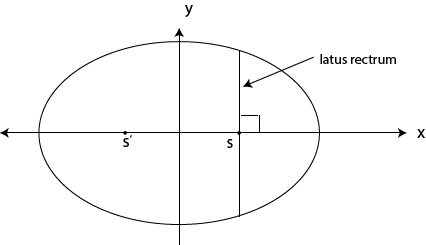
          Note:

          Latus rectum is always parallel to the directrix

VII.  VERTEX

This is the turning point of the conic section.

For parabola

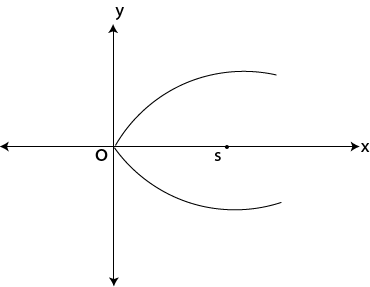
0 – is the vertex

For ellipse

Where V and V¹ is the vertex of an ellipse

PARABOLA

This is the conic section whose eccentricity, e is one i.e. e = 1

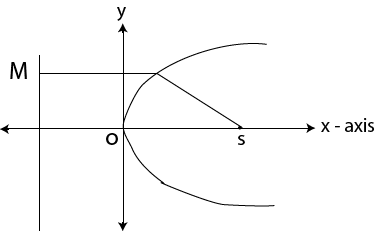
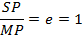
                    For parabola

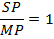
SP = MP

      EQUATIONS OF THE PARABOLA

These are;

a) Standard equation

b) General equations

A. STANDARD EQUATION OF THE PARABOLA

1^st case: Along the x – axis

·         Consider the parabola whose focus is S(a, 0) and directrix x = -a

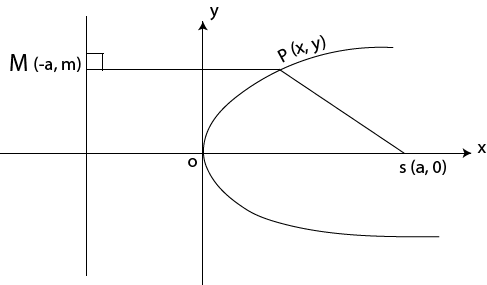
          Squaring both sides

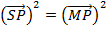
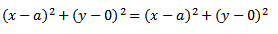
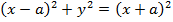
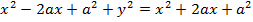
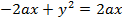
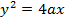
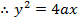
Is the standard equation of the parabola

PROPERTIES

i) The parabola lies along x – axis

ii) Focus, s (a, o)

iii) Directrix x = -a

iv)  Vertex (0, 0) origin

Note:

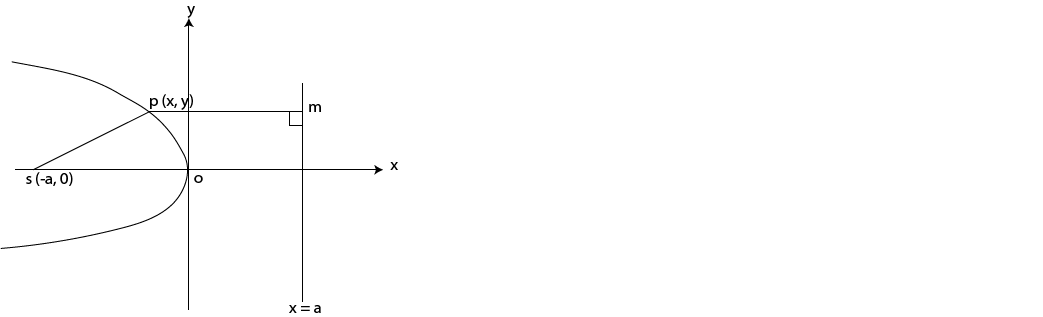
PROPERTIES

1) The parabola lies along x – axis

2) Focus s (-a, o)

3) Directrix x = a

4) Vertex (o, o) origin

2^nd case: along y – axis

Consider the parabola when focus is s (o, a) and directrix y = -a

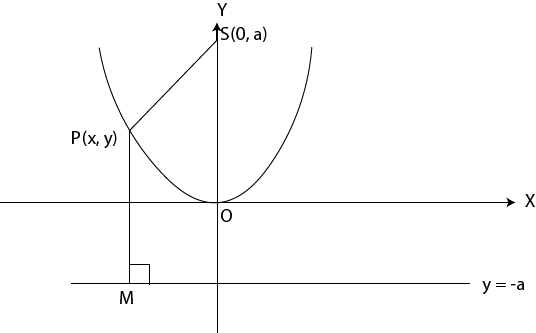
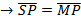
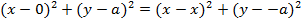
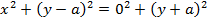
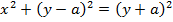
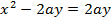
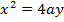
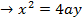
·         Is the standard equation of the parabola along y – axis

PROPERTIES

i) The parabola lies along y – axis

ii) The focus s (o, a)

iii)  Directrix y = -a

iv)  Vertex (o, o) origin

Note;

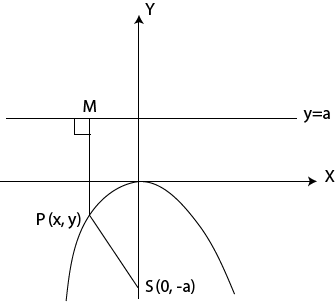
Hence,    x² = -4ay

PROPERTIES

i) The parabola lies along y – axis

ii) Focus s (o, -a)

iii) Directrix y = a

iv) Vertex (o, o)