ADVANCED MATHEMATICS FORM 6 – COMPLEX NUMBER

The solution of a quadratic equation 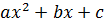can be obtained by the formula.

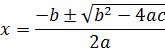
Example

i) If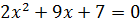

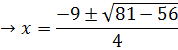
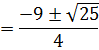
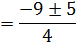
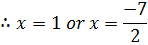
This is straight forward enough.

ii) If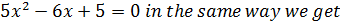

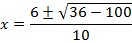
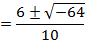
In fact 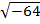 cannot be represented by an ordinary number.

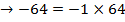
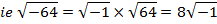
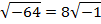
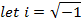
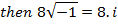
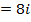
Similarly,

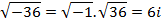
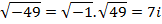
Then from the equation that we have been solving it gives that

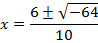
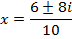
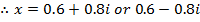
Since 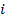 stand for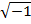

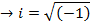
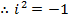
Note that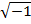

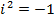
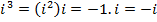
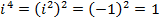
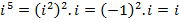
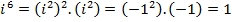
The power of 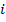 reduces to one of

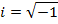
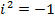
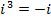
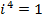
It can be deduced that

Numbers of the form 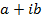,where a and b are real numbers are called complex numbers.

Note that 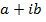cannot be combined any further

In such expression

A is called the real part of a complex number

B is called imaginary part of a complex number (NOT )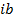

Complex number = (real part) + (imaginary part)

OPERATION ON COMPLEX NUMBERS

ADDITION AND SUBTRACTION

Examples:

1.

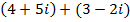
Solution

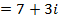
2. 

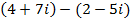
    Solution

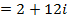
So in general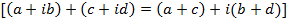

EXERCISE

I.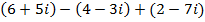

II.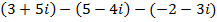  

MULTIPLICATION OF COMPLEX NUMBERS

Example:
1.  
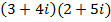
Solution

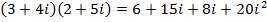
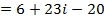
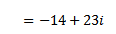
2.  

 Solution

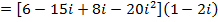
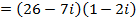
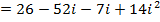
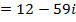
3.  

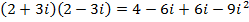
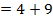
             = 13

Any pair of complex numbers of the form  has a product which is real.

i.e.

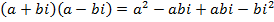
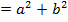
Such complex numbers are said to be conjugate

Each is a conjugate of the other.

Hence

i.e.

.if  then the conjugate is

A division will be done by multiplying numerator and denominator the conjugate of the denominator.

Example

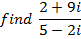
For division, the numerator and denominator both will be multiplied by the conjugate of the denominator.

i.e. 

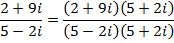
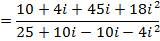
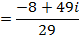
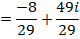
NOTE: – The complex number is zero if and only if the real term and the imaginary term are each zero.
– The real term is given first even when is negative

i.e. 

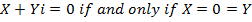
Suppose

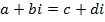
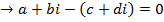
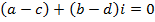
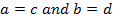
Thus two complex numbers are equal if and only if the real terms and the imaginary terms are separately equal.

Example:

Find the value of x and y if

a)

Solution

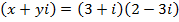
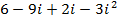
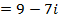
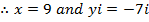
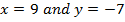
b)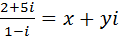  

Solution

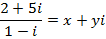
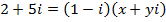
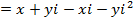
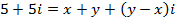
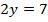
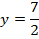
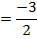
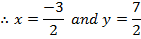
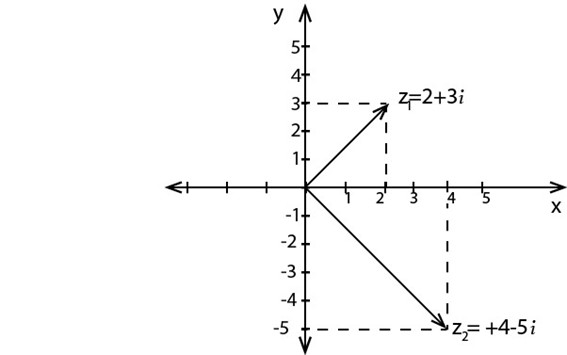
GRAPHICAL REPRESENTATION OF COMPLEX NUMBERS

Consider the reference line denoted by XX₁ and YY₁

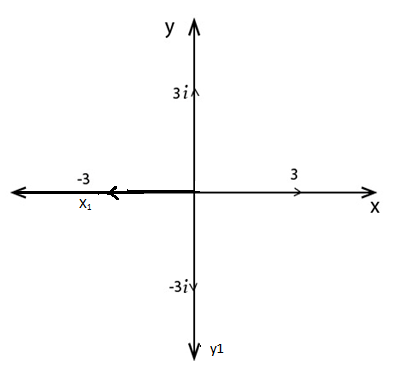
i) x- axis represents real number (i.e. XX₁ is called real axis

ii) y- axis represents imaginary number (YY₁ is called imaginary axis

ARGAND DIAGRAM

If 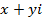 is a complex number this can be represented by the line  where P is the point (x, y)

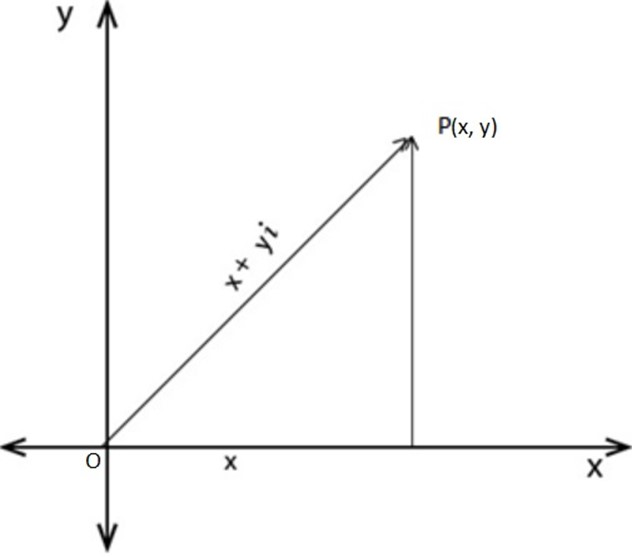
This graphical representation constitutes an Argand diagram

Example:

Draw an Argand diagram to represent the vectors

i)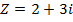

ii)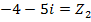

Z is often used to denote a complex

Solution

Using the same XY – plane