INTRODUCTION
A three dimensional figure is a solid figure having three measures.
Some examples are pyramids, cylinders, prisms, cubes and cuboids.

– Apart from three dimensional figures, there are also one and two dimensional figures.
Examples
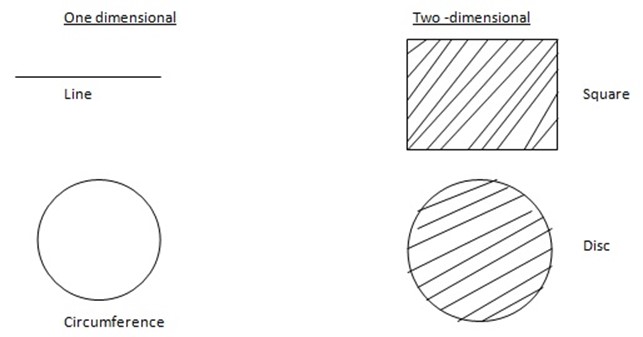
1. A line is one – dimensional. There is one direction to move along it. (up or down it).
2. A flat shape is two- dimensional. There are two directions to move across it (up or down, and left or right).
The diagram below show objects which are one or two –dimensional.
-The –dimensional space contains line and planes. Consider a diagram of a cube: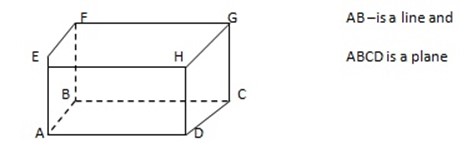
Note:
When we refer to a cube or cuboid ABCDEFGH, then ABCD and EFGH are apposite faces, with, E opposite A, F opposite B and so on , as in the diagram above
– Line and planes can be parallel or perpendicular. In the diagram above:
· The lines AD and EH are parallel.
· The lines AD and AE are perpendicular.
· The planes ABCD and EFGH are parallel
· The planes ABCD and AEHD are perpendicular
· The lines AD and CE are neither parallel nor perpendicular and the planes ABCD and EHCB are neither parallel nor perpendicular
EXERCISE 3.1A
The diagram show a cube ABCDEFGH. The face ABCD is horizontal. Give
a) (a) Another horizontal face
b) (b)A vertical face
c) (c)A horizontal line
d) (d)A vertical line
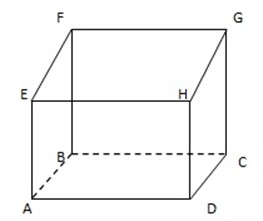
2. Refer to the diagram for question. Write down
a) Two faces which meet at GC
b) Three edge which meet at F
CLASSIFYING THREE-DIMENSIONAL FIGURES
Definitions:
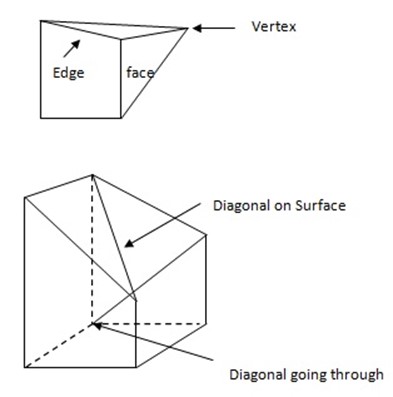
1. 1) A polyhedron is a solid whose surface consists of flat polygons.
2. 2 )A face is a flat surface of a solid.
3. 3)An edge is a line where two faces meet.
4. 4)A vertex is a point where three or more faces meet.
5. 5)A diagonal is a line joining two vertices which is not an edge. A diagonal may go through the solid or be an its surface.
CUBOID
A cuboid is a box shape with faces that are rectangles. The diagram show a cuboid ABCDEFGH. All are rectangles that are parallel or perpendicular to each other.
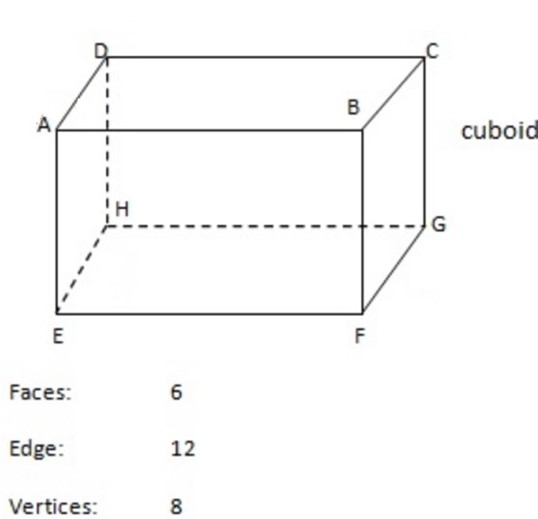
-AG and BG are diagonals. AG goes through the solid, and GB lies on its surface.
CUBE
-A cube is a cuboid with all edges the same length. All the faces are squares.
PRISM
-A prism is a solid which has the same cross- section through. A triangular prism has a triangular cross-section
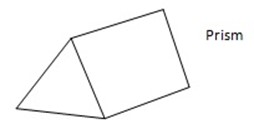
Faces: 5
Edges: 9
Vertices: 6
PYRAMID
A pyramid has a flat base in the shape of a polygons and all other edges come to a point called the vertex
TYPES OF PYRAMID
1. 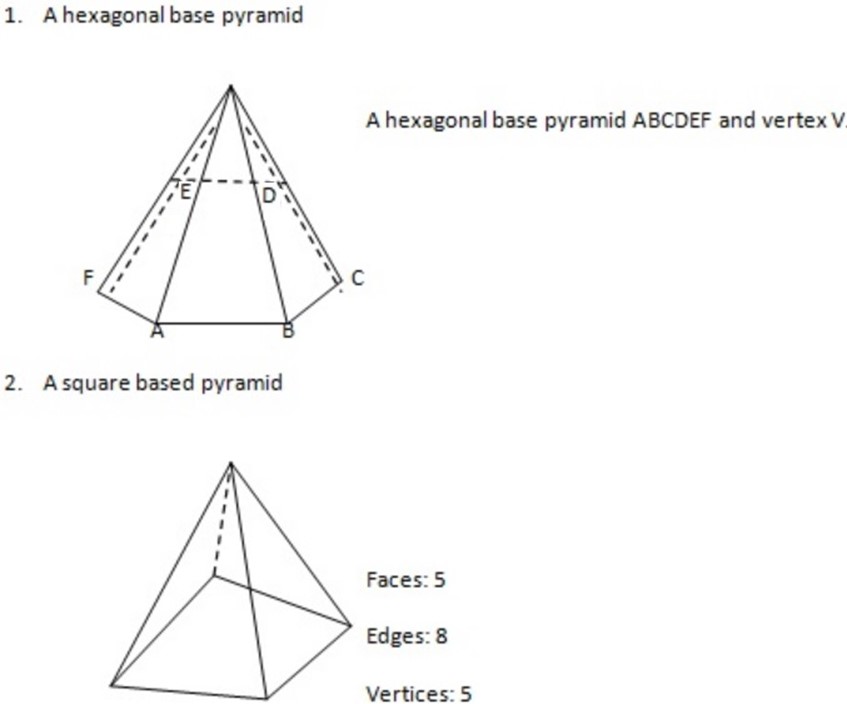
-If the vertex of the pyramid is above the centre of the base it is a right pyramid.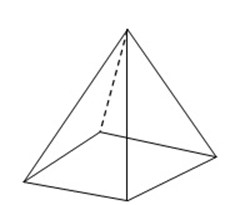
EXERCISE 3.1B
1. 1) Find everyday objects in the shape of
(a) a cuboid (b) a cube (c) a prism
2. 2)What are the mathematical names for the shapes of these objects?
(a) a match box (b) a football (c) an unsharpened pencil (d) the tip of a sharpened pencil.
CONSTRUCTION OF THREE-DIMENSIONAL FIGURES
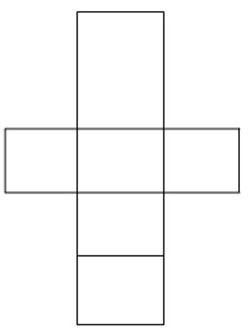
-You can make a model of a solid out of paper. The shape that you cut out is a net. The diagram show a net for a cube.
Notice that:
There are six squares for the six faces of the cube
-There are many possible different nets for the same object. The nets below will also make a cube.
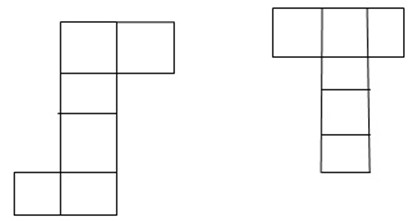
EXERCISE 3.2.A
Make nets for solids and construct the shapes
2)What sort of solid will be made from each of these net?
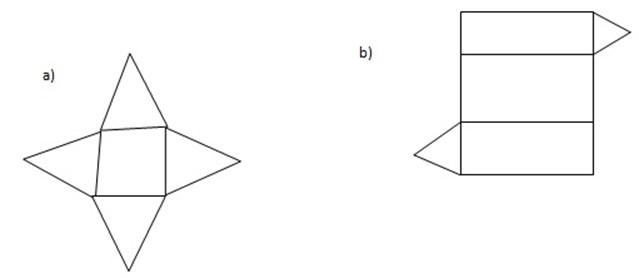
SKETCHING THREE-DIMENSIONAL FIGURES
-We can represent a three-dimensional object in two dimensional object in two dimensional.
I. By the use of oblique projection.
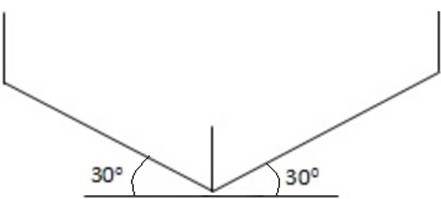
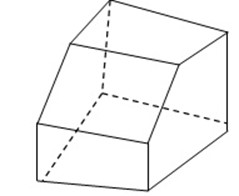
Look at the solid shown below: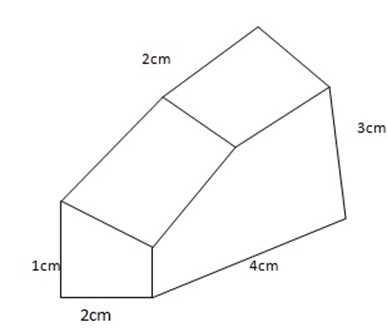
-It is not drawn to scale.
-The following steps will give an accurate representation
i. Draw the base lines first at 300 to the horizontal. Then add the vertical lines. There are all parallel.
ii. Now add any top edges, noting that all edges that are parallel will still be parallel in the oblique projection.
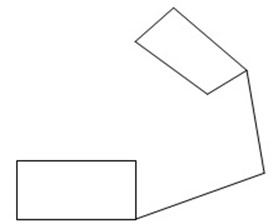
iii. You can now draw the sloping edges, together with any hidden edges that are drawn as dotted lines. The find diagram is now shown.
II. By the use of Isometric paper
-There is special paper to make drawing solids easier. This is Isometric paper. On this paper there are lines at 600 to each other these lines to draw solids.
-Sometimes this paper has dots instead of lines
– – On a special grid the shape above looks like the diagram below
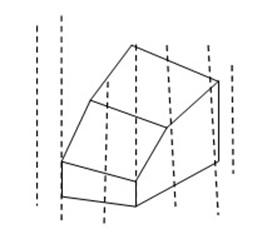
Exercise 3.3A
1. 1) The diagram show a cube ABCDEFGH drawn in oblique projection
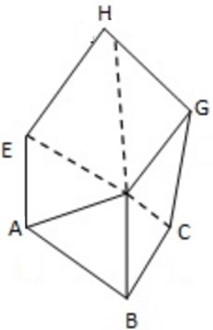
Write down
a) a)Two faces.
b) b)Two edges.
c) c) Two diagonals that pass through the shape.
d) d)Two diagonals that lie on the surface of the shape.
ANGLE BETWEEN LINE AND PLANE
Example
VABCD is a pyramid, with VA= VB=VC=VD=5cm and ABCD a square of side 4cm. Find the angle between VA and ABCD.
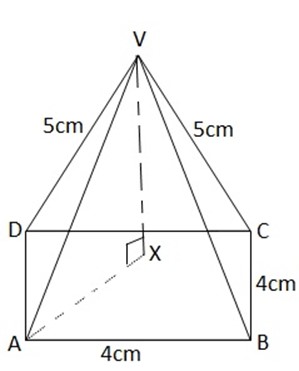
Solution
-Drop a perpendicular from V to ABCD. This meets ABCD at x, the centre of the square. So the projection of VA on ABCD is AX . The angle we want is <VAX.
By Pythagoras theorem in ΔABC
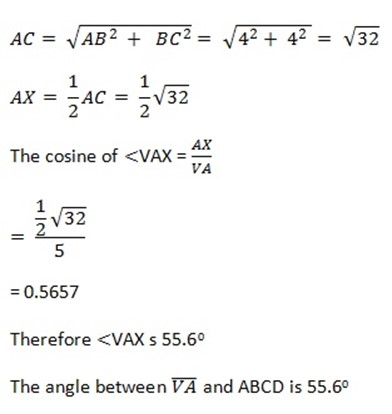
EXERCISE 3.3B
1. 1) ABCDEFGH is a cube with a side of 4cm. Find the angle between the line AG and the face ABCD
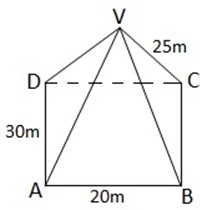
2. 2) VABCD is a pyramid with a rectangular base ABCD. AB=20M, AD=30M and VA=VB=VC=VD=25M. Find the angle between VA and ABCD
ANGLE BETWEEN TWO PLANES
Example
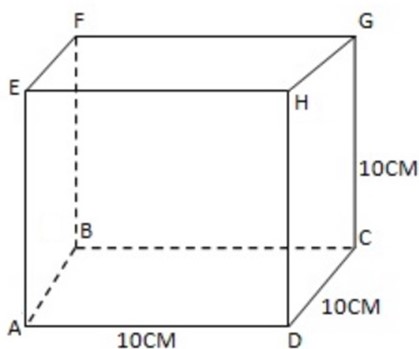
The diagram show a cube ABCDEFGH of side 10cm. Find the angles between
a) a) ABCD and ABGH F G
b) b) FHA and FHDB
Solution
A) a)The planes meet in the line AB.
-AD is a line in ABCD which is perpendicular to AB.
-AH is a line in ABGH which is perpendicular to AB. So the angle we want is the angle between AD and AH Which is < DAH.
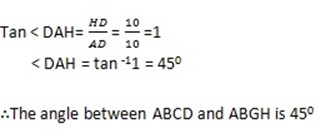
b). The planes meet in the line FH.
Let x be the midpoint of FH, and let p be the midpoint of BD
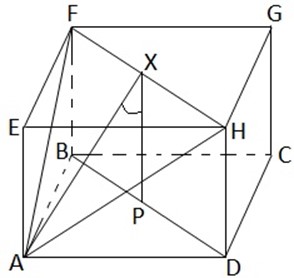
-Then XA is a line in FHA which is perpendicular to FH.XP is a line FHDB which is perpendicular to FH
-So the angle we want is the angle between XA and XP, which is <AXP.
-XP is the height of the cube: which is 10cm.
-AP is half the diagonal of ABCD ie

EXERCISE 3.3C
1. The diagram show a pyramid VABCD in which ABCD is a square of side 20m, and VA= VB=VC=VD=15m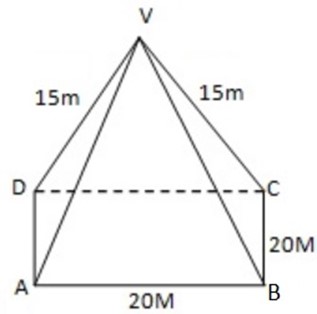
Find the angles between the planes
a) VAB and ABCD
b) VAB and VCD
2. 2) A prism has length 8cm, and its cross- section is an equilateral triangle of side 5cm. Find angles between the planes.
a) ADEB and BEFC
b) AEF ad BEFC
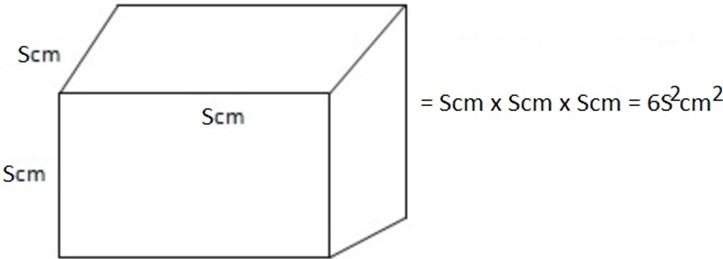
SURFACE AREA OF THREE-DIMENSIONAL FIGURES
Consider the diagram which shows a cube of 5cm . It has 6 faces, which are squares of side 5cm. So the total surface area is
2. Consider the diagram which show a cuboid which is a cm by b cm by c cm. It has 6 faces which are rectangles: two are a cm by b cm, two are b cm by c cm and two are c cm by a cm. so its total surface area is
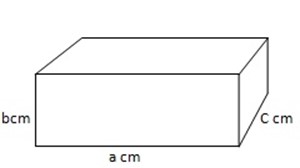
=(a cm × b cm)×2+ (b cm × c cm) x 2 + (a cm× c cm)×2
=2ab cm2 + 2bc cm2+2ac cm2
=(2ab+2bc+2ac)cm2
Example 1:
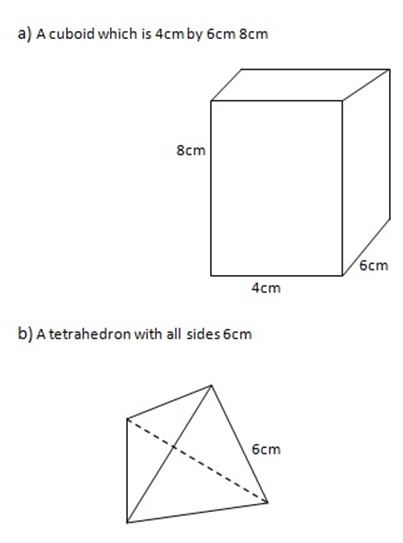
Find the surface area of a cuboid which is 12cm by 10cm by 8cm.
Solution:
Given:
a = 12cm, b = 10cm and c = 8cm
Formula = (2ab+2bc)cm2
=(2×12×10)+(2×10×8)+(2×12×8)
= 240 + 160 = 192
= 592
The surface area is 592cm2
EXERCISE 3.4A
1. 1. A tea crate has a square base of side 0.8m, and its height is 1.1m. Find the surface area of the crate.
2. 2. A room is 5.2m long, 2.5m high and 4.5m wide. Find the surface area of the wall and the wiling.
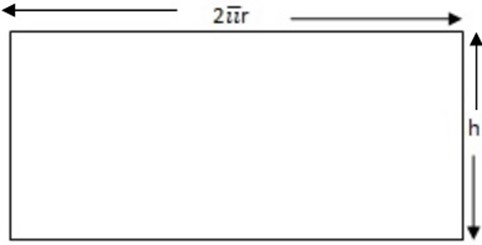
CYLINDER
The diagram show a cylinder, which has height him and top radius r cm.
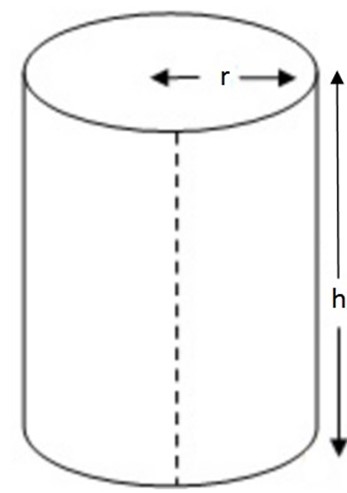
– – The surface of a cylinder consists of a circular top and bottom, and curved side.
– -Imagine cutting the cylinder down the side, and unfolding it. The curved side becomes a rectangle, with height h and width the circumference of the cylinder.

Example
Find the curved surface area of a cylinder which is 6cm high and with radius 4cm.
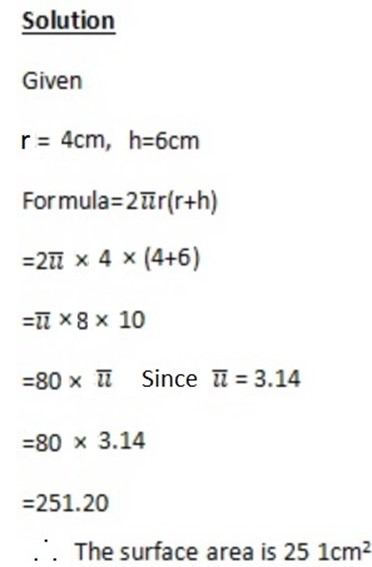
EXERCISE 3.4 B
1. A tin of shoe polish is 2cm high and 4cm in radius. Find its surface area.
2. A paint roller is a cylinder which is 15cm long and with radius 3cm. Find the area of wall it can cover in one revolution
PRISMS
– Recall that a prism is a solid with a constant cross section
– In many cases the cross-section is a triangle.
– The surface of a prism consists of the two cross-sections and the sides. In particular, the surface of a triangular and the sides. In particular, the surface of a triangular prism consists of two triangles and three rectangles.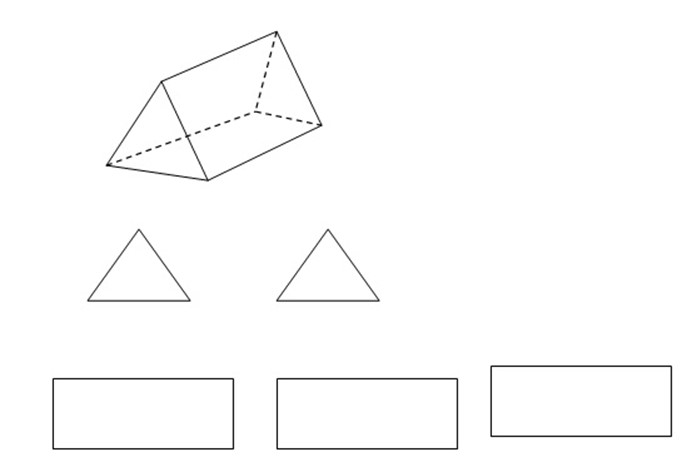
Example
A prism has a cross-section which is a triangle with sides 5cm, 12cm and and 13cm. Its length is 10cm. Find Its surface area
Solution.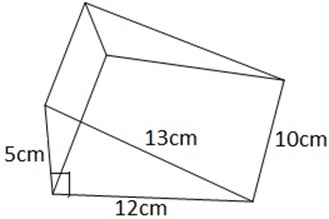
-The surface consists of:
· . Two triangles of side 5,12and 13
· . Three rectangles: 5, by 10, 12 by 10 and 13 by 10
Note:
The two triangles are right angled.
– The area of each triangle is
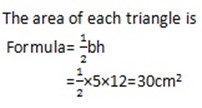
The areas of the rectangle are: Formula=l ×w
=(50×10)+ (12×10) =(13×10)
=50 +120+130
=300cm2
-Total area =(2×30)+300
=60+300
=360cm2
The surface area is 360cm2
EXERCISE 3.4C
Find the surface area of the prisms shown below
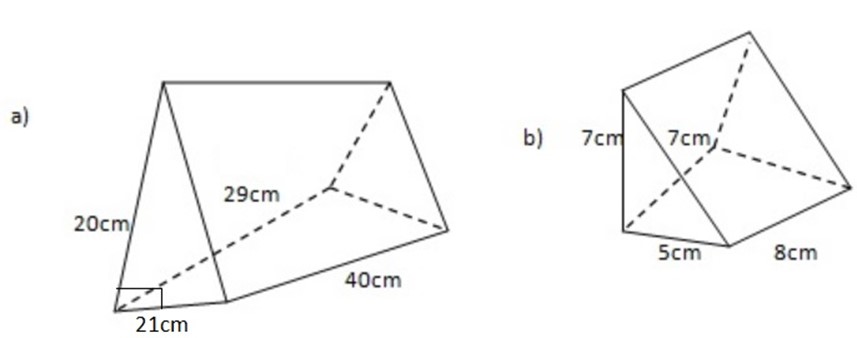
2.The cross-section of a prism is a regular pentagon of side 8cm. The prism is 30cm long. Find the surface area of the prism.
PYRAMIDS
The surface area of a pyramid is the sum of the base area and the area of the triangular sides. Sometimes you need to use Pythagoras’ theorem to find the area of the sides. The following example shows the method.
Example
A pyramid has a square base of side 10cm and height 15cm.
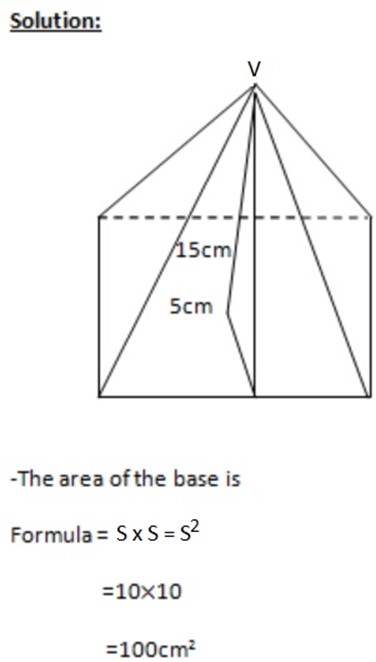
– Take a line from the vertex V to the middle of one of the sides of the base. The vertical rise of this line is 15cm.
– The horizontal run of this line is 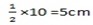
– Hence the length of the line is
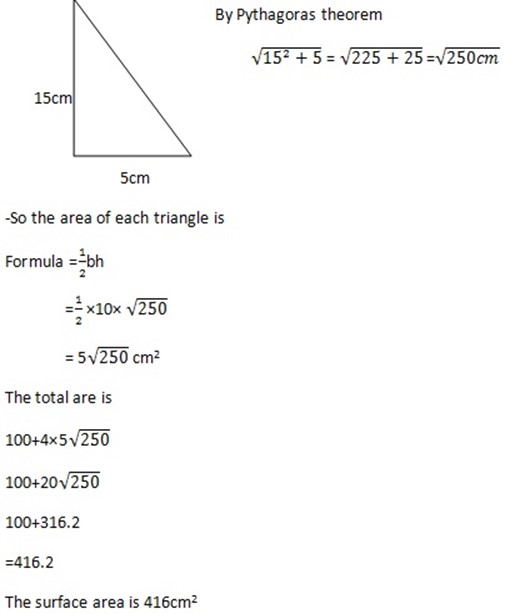
Exercise 3.4 D
1. A pyramid has a square base of side 10cm and height 12cm. Find the surface area of its triangular faces.
2. A pyramid has a rectangular base which is 40cm by 60cm. Its vertex is 20cm above the centre of the base. Find the total surface area of the pyramid.
CONES
-The height h, of a cone is its perpendicular height. It is not the length of the slanting edge.
-The length of the slanting edge, l is given by Pythagoras’ theorem.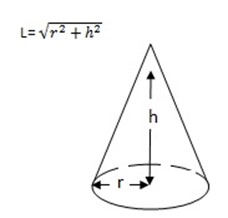
-Imagine cutting along the side of the cone unfolding. You would get a sector of a circle. The radius of this circle is l and the arc length is the circumference of the cone base, 2πr. Hence the area of the curved side, which is the area of this sector, is the area of the circle, πl2
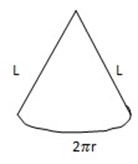
π L2 Is reduce in the ratio of the circumference of the cone base and the complete circle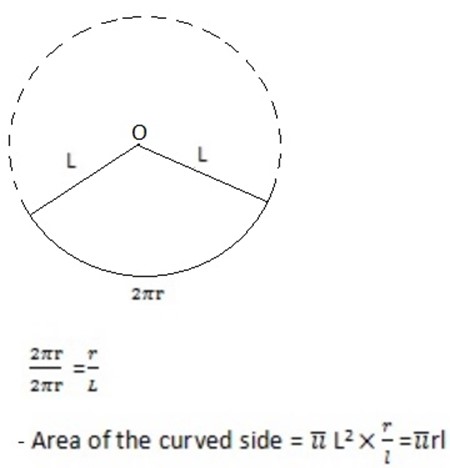
∴ The total area of the cone is
πr2 + πrl = πr(r+L)
Example
A cone has base radius 4cm and height 3cm . Find its curved surface area.
Solution
The slant height l is l is given by

EXERCISE 3.4E
Find the surface area of these cones.
a) a) With base radius 5cm and height 12cm.
b) b) With base radius 7m and height24m
2.The base radius of a cone is c cm and its surface area is 160 cm2. Find its slant height and hence find its height.
SPHERES
-A sphere is a round solid, like a ball.
If the sphere has radius r, then its surface area A is
A = 4π2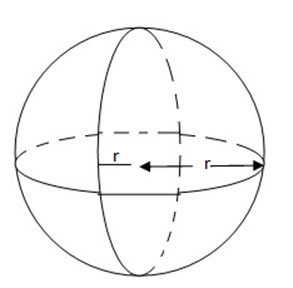
Example
Find the surface area of sphere of radius 0.46m
Solution
Given,
Radius r = 0.46
Area = 4π2
= 4× π(46)2
= 2.660
∴ The surface area is 2.66m2
EXERCISE 3.4F
1. Find the radio of the spheres with area
a) a) 64πcm b) 0.44m2
2. A sphere has surface area 48cm2. Find its radius
VOLUMES OF THREE – DIMENSIONAL FIGURES
PRISMS
Recall that a prism is a solid with a constant cross-section.
If the area of cross –section is A and the height is h, then the volume is
V=Ah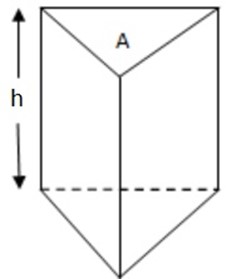
– The cuboid and the cylinder are examples of prisms. The volume of a cuboid is given by
V = lbh (The cross –section is a circle)
– The volume of a cylinder is given by
V= πr h (The cross –section is a circle)
– For both of these solids, the volume is given by
V= Ah, where A is the area of cross-section.
Example
The cross-section of a right angled prism is a triangle for which the shorter are 5cm and 6cm . The prism is 20cm long . Find its volume
Solution: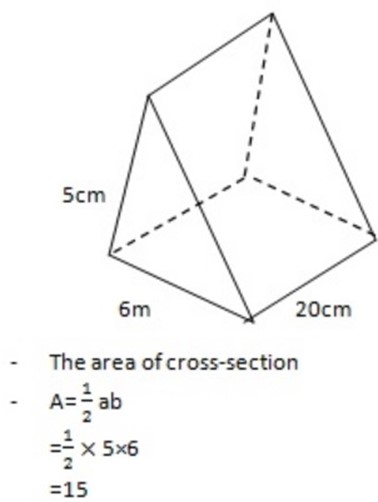
– Now multiply by the height
Volume = 20×15
= 300
∴ There volume is 300cm3
EXERCISE 3.5.A
1. 1. The cross-section of a prism is a regular hexagen with side 0.8m. The prime is 1.6 long. Find the volume of the prism.
2. 2. The cross-section of a prism is a right angled triangle with sides 12cm, 9cm and 15cm, and with height 25cm. Find the volume of the prism.
PYRAMIDS AND CONES
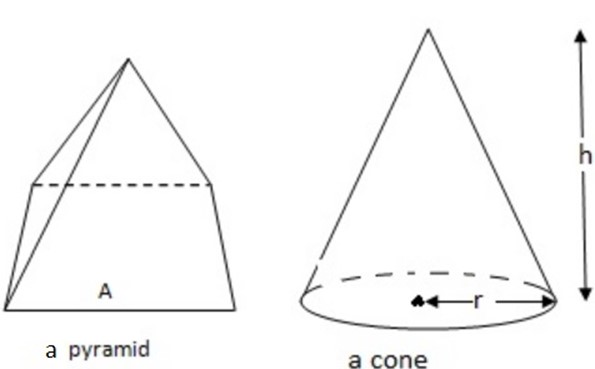
– The pyramid tapers to a point from a base, which is usually a rectangle.
– The cone tapers to a point from a base, which is a circle.
– For both these solids, the volume is a third that of the corresponding prism with the same base. The volume of a pyramid is a third of the corresponding cuboid
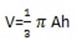
∴ The volume of a cone is a third that of the corresponding cylinder
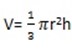
Example
A pyramid has a square base. Its height is 7cm and its volume is 56cm3. Find the side of the base.
Solution
– Suppose the side of the base is x2 cm2
– Formula for the volume of a pyramid

∴ The side of the base is 4.9cm
EXERCISE 3.5.B
1. 1. A pyramid has a square base of side 10cm and volume 500cm3. Find its height.
2. 2. A cone has height 12cm and volume 50cm3. Find its base radius.
SPHERES
If a sphere has radius r, then its volume is
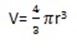
Example 1:
A sphere has radius 8.7cm. Find its volume.
Solution
Apply the formula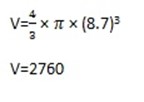
∴ The volume is 2760cm3
Example 2.
A sphere has volume 100cm3. Find its radius
Solution
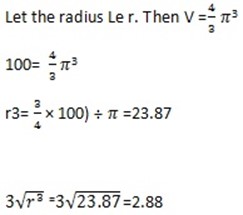
∴ The radius is 2.88m
EXERCISE 3.5C
1. 1. A sphere has volume 1.6m3
a) Find its radius.
b) Find its surface area.
2. 2. A sphere has surface area 56cm2
a) Find its radius
b) Find its volume
SOLUTIONS
EXERCISE 3.1.A
1. a) EFGH b) HDCG c) AD d)EA
2. a) GCDH and GCBF b)FG,FE and FB
EXERCISE 3.1 B
1. a) A Match box b) A die
2. a)Cuboid b) Sphere c) Cylinder d)Cone
EXERCISE 3.2A
1. 1. a)
b)
2. 2. a) A pyramid
b) A prism
EXERCISE 3.3A
1. a) ABCD and BCGF
b) AB and DC
c) EC and AG
d) EB and FC
EXERCISE 3.3.B
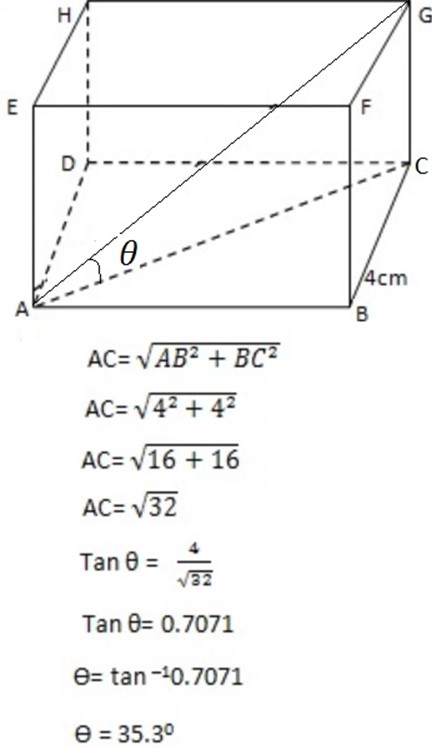
∴ The angle between the line AG and the face ABCD is 35.30
2. 2. Given
AB=20M, AD=30m and VA =VB=VC=VD=25m
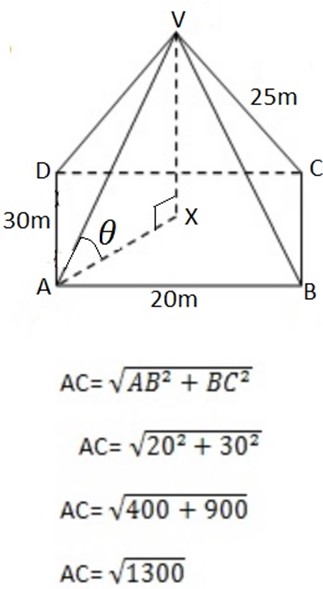
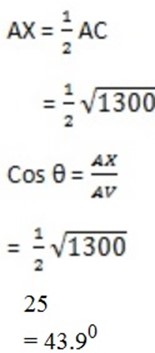
∴ The angle between V A and ABCD is 43.90
EXERCISE 3.3C
Given
– A square base of side 20m
– VA = =VC=VD =15M
– Angle between the planes VAB and ABCD = ?
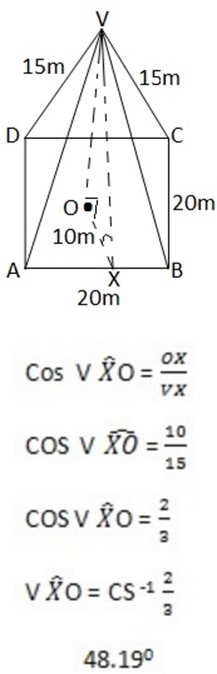
∴ The angle between the planes VAB and ABCD is 48.190
2. Given
– Length of the prism 8cm
– Side of the triangle 5cm
– Angle between the planes ADEB and BEFC =?
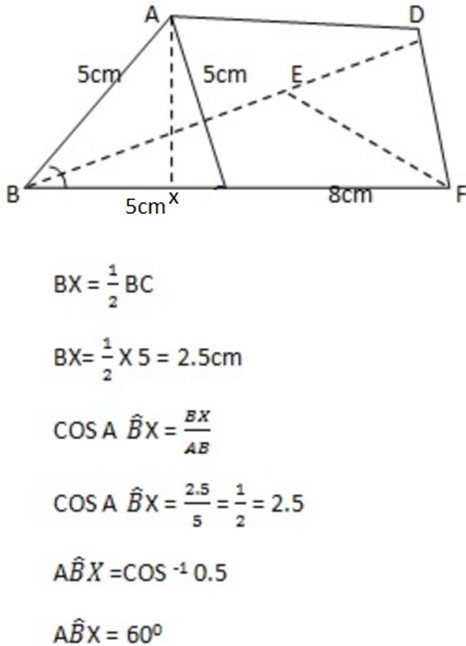
∴ The angle between the planes ADEB and BEFC is 600
EXERCISE 3.4A
1. Given
1. A square base of side 0.8m and height 1.1m
Formula = Base area = (0.8×0.8)×2
= 0.64 ×2
= 1.28
Then other areas
= (0.8 ×1.1) ×4=3.52
– The total area = 1.28 + 3.52=4.8
∴ The surface area of the crate 4.8m2
2. Given
– A room with length = 5.2m, height=2.5m and width= 4.5m
-The area of the wall = length × width
= 5.2 × 4.5
= 23.4 m2
– The area of the wall =(height × length) ×2 + (height ×width)×2
= (2.5×5.2)x2 + (2.5×4.5 )×2
= 26+22.5
= 48.5m2
– The total area = 23.4m2 + 48.5m
= 71.9m2
∴ The surface are of the wall and the wiling is 71.9m2
EXERCISE 3.4B
1. 1. Given
– Height = 2cm
– Radius = 4cm
– Formula = 2 πr (r+h)
= 2 π×4(4+2)
= 8π×6
= 48π
=150.72
∴The surface area is 151cm2
2. Given
Length =15cm
Radius=3cm
Area of the wall = length × width
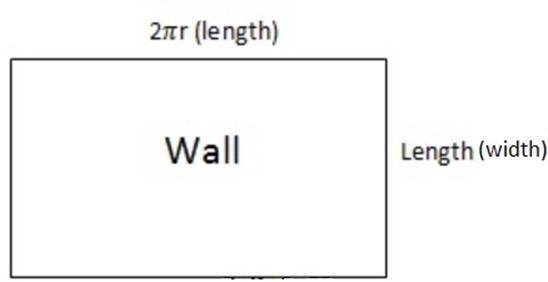
Area of the wall = 2πr ×L
=2×π×3×15
= 90 π
= 282.6cm2
EXERCISE 3.4C
1. a)surface area of the prisms=
– Base area = Rectangle=L×W
-The area of rectangle are
=(21×40) + (29×40)
=840 ×1,160 +800
=2,800cm2
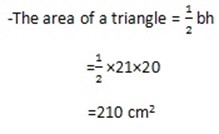
But the prism have 2 triangles
210×2 = 420cm2
-The total area is 2,8000+420=3,220
The surface area of the prism is 3,220cm2
Given
Side = 8cm
Length=30cm
-A regular pentagon has 5 sides
-Area of a regular pentagon has 5 rectangles which are equal.
– The area of rectangles are
Formula = L×n
= (30×8)×5
=240×5
=1,200cm2
Base area
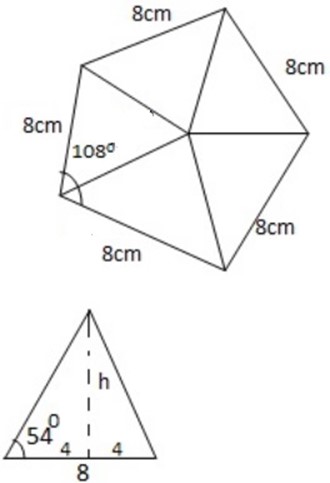
–

– For base areas, that is top and bottom area there are 10 triangles.
– Therefore 22.0224×10=220.224 = 220
Hence
The total area = 1,200 + 220 = 1,420cm2
∴ The surface area of the prism is 1420cm2
EXERCISE 3.4 D
Given
-A square base of side = 10cm and height is 12cm. the base area =5×5=50
=10×10
=1002
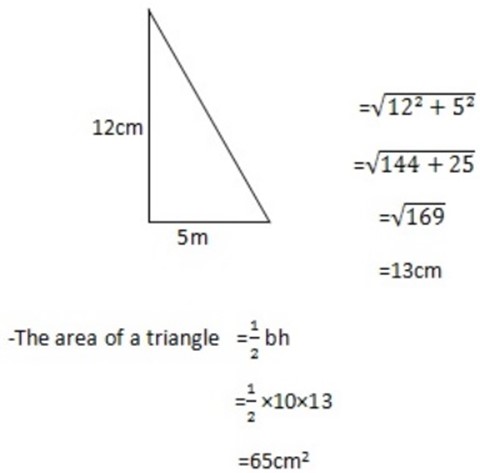
– Total are of all triangles 65cm2 × 4 = 260cm2
∴ The surface area of triangular faces is 260cm2
EXERCISE 3.4
a) Formula for