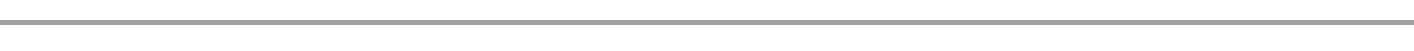Operations on matrices
A matrix represents another way of writing information. Here the information is written as rectangular array. For example two students Juma and Anna sit a math Exam and an English Exam. Juma scores 92% and 85%, while Anna scores 66% and 86%. This can be written as.

A size of a matrix is known as its order and is denoted by the number of rows times the number of columns. Therefore the order of above matrix is 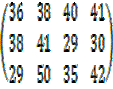 each of the numbers in the matrix is called an element.
each of the numbers in the matrix is called an element.
Types of matrix
(i) Row matrix. This is a matrix having only one row. Thus 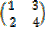 is a row matrix.
is a row matrix.
(ii) Column matrix. This is a matrix having only one column. Thus 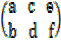 is a column matrix.
is a column matrix.
(iii) Null matrix. This is a matrix with all its elements zero. Thus  is a null matrix or zero matrix.
is a null matrix or zero matrix.
(iv) Square matrix. This is a matrix having the same number of rows and column. Thus 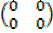 is a square matrix.
is a square matrix.
(v) Diagonal matrix. This is a square matrix in which all the elements are zero except the diagonal elements. Thus 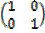 is a diagonal matrix.
is a diagonal matrix.
Note that: The diagonal in a matrix always runs from up left to lower right.
(vi) Unit matrix of identity matrix. This is a diagonal or square matrix in which the diagonal elements equal to 1. An identity matrix is usually denoted by the symbol I. Thus
I = 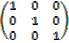
(vii) Equal matrix. Two matrices are said to be equal if they are of the some order, responding elements are equal.
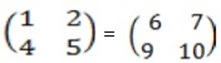
An m x n matrix (E.g. matrix A) is a rectangular array of m x n real (or complex numbers) arranged in M horizontal rows and n vertical columns.
A =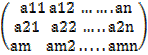
Example
1. The table below represents number of students in each stream in each form. Now write that information in matrix.
|
Form |
I |
II |
III |
IV |
|
Stream J |
36 |
38 |
30 |
41 |
|
Stream K |
38 |
41 |
29 |
30 |
|
Stream L |
29 |
50 |
35 |
42 |
edu.uptymez.com
J = 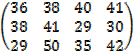
2. Give the order of the following matrices.
i.A = 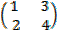
has order 2×2
ii.B = 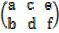
has order 2×3
iii. C = (P Q) has order 1×2
iv. D = 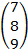
has order 3×1
SPECIAL MATRICES
Is the matrix having all elements zero ( zero matrix)
Z = 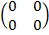
IDENTITY MATRIX: Is the square matrix whose elements is the leading diagonal are everywhere 1 and 0 elsewhere.
I = 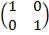 .
.
= 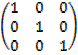
Identity matrix
ADDITION OF MATRICES
Matrix addition is performed by adding corresponding elements.
for example
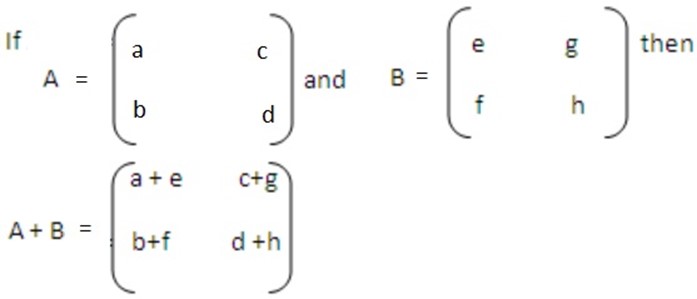
Example
1. Given matrices A = (1 2 3) and B = ( 4 5 6)
Find
i. A + B
ii. B + A
Solution
i. A + B = ( 1 2 3) + ( 4 5 6)
= ( 1+4 2+5 3+6)
= ( 5 7 9)
ii. B + A = ( 4 5 6 ) + ( 1 2 3 )
= ( 4+1 5+2 6+3)
= (5 7 9)
2. If A = 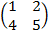 and B =
and B = 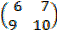
Then, find A + B
A + B = 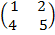 +
+ 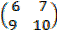
= 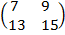
ADDITIVE IDENTITY MATRIX
Consider any 2 x 2 matrix 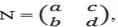 N = , where a, b, c, and dare any real number. If N + Y = Y + N = N, then N
N = , where a, b, c, and dare any real number. If N + Y = Y + N = N, then N
is the addictive identity matrix.
The 2 x 2 addictive identity matrix is 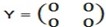
Let matrix A = 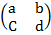
And Z = 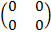
Then Z is an additive identity matrix.
i.e. A+Z = A and Z +A = A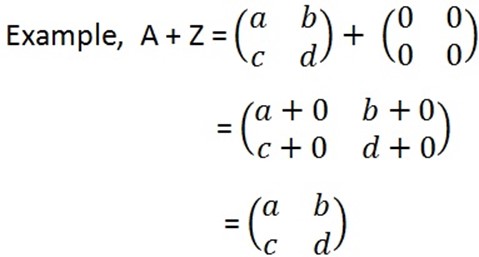
ADDITIVE INVERSE MATRIX
Consider any two matrices of the same order P and Q.
If P + Q = Q + P = R, then Q is called the additive inverse of P or P is called the additive inverse of Q.
i.e. Q = -P or P = -Q
Suppose,
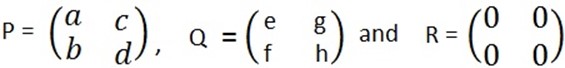
If P + Q = Z then,
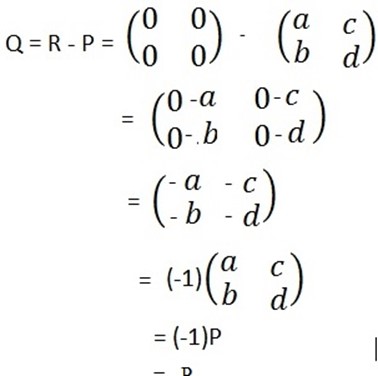
= -P
Therefore the additive inverse of P is -P
Example
1. Find the additive inverse of
(a) B = 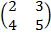 (b) C=
(b) C= 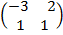
Solution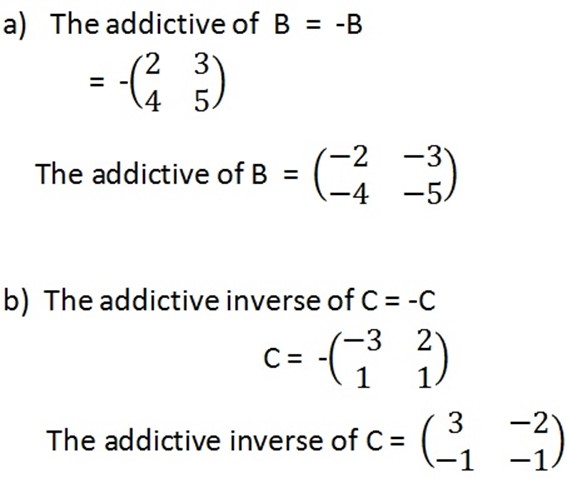
SUBTRACTION OF MATRICES
The process of subtracting a real number “f” from another real number g is the same as adding g to the additive inverse of f.
Thus f-g = f + (-g).
NOTE
When matrix P is subtracted from another matrix Q the result is the same as adding P to the additive inverse of Q.
i.e P- Q = P + (-Q).

SCALAR MULTIPLICATION OF MATRICES

Example If B = 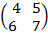
i. Find 2B
Solution
2 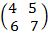 =
= 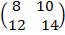
ii. Find 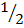 B
B
Solution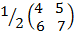 =
= 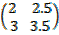
Questions
1. Given;
A = 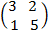 B =
B = 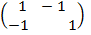 C =
C = 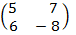
FIND.
(a) 3A + 2B
Solution
3A = 3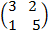
3A = 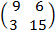
2B = 2 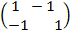
2B = 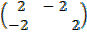
3A+ 2B = 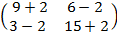
= 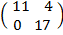
(b) 5 ( A + B)
A+ B = 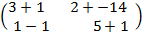 =
= 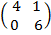
5(A+B) = 5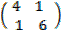
= 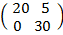
2. Using the matrices;
A = 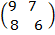 , B =
, B = 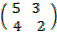 and C =
and C = 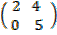
a) Find A (BC)
BC = 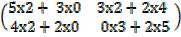
BC = 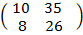
A (BC) = 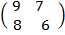
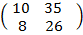
= 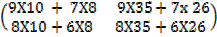
= 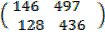
b) (AB ) C
AB = 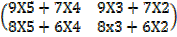
AB = 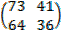
C = 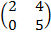
(AB)C = 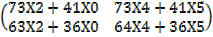
(AB)C = 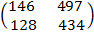
DETERMINANT OF A MATRIX

NOTE
Determinants exist for square materials only.
Calculate the determinant of a matrix and tell whether the matrix is singular or non singular.
1. A = 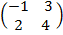
Solution
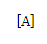 = (-1 x4) – (2×3)
= (-1 x4) – (2×3)
= -4 -6
= -10
A is non singular matrix.
Inverse of matrices
The inverse of a matrix say P is another matrix denoted by P-1

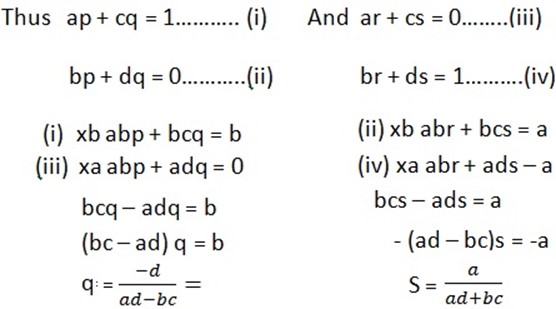
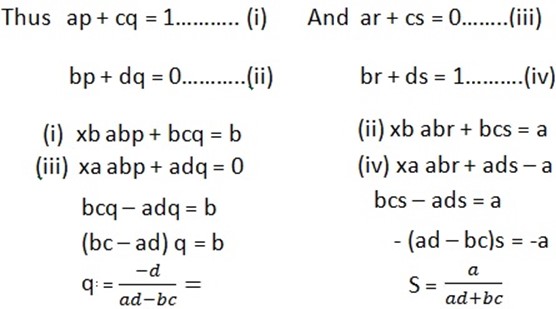

NOTE

Can be found by interchanging the elements of the leading diagonal so that d takes place of a and a takes place of d. Change the sign of the elements in the main diagonal so that b and c becomes –b and –c respectively.
Divide each element by the determinant of A
2. Inverse exist for non singular matrix.
3. Singular matrix has no inverse because they have zero determinant.
Example
Determine the inverse of the gives matrix and indicate if it is singular or non singular.
1. A = 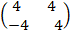
Solution
Determinant; (A) = (4×4) – (-4×4)
= 16+16
= 32
A-1 = 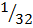
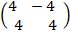
A-1 = 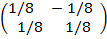
A is non singular matrix.
2. B = 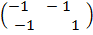
Solution
Determinant ( B ) = (-1×1) – (-1x-1)
= -1-1
= -2
B -1 = -1/2 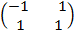
B-1 = 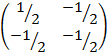
MATRICES ON SOLVING SIMULTANEOUS EQUATIONS
Questions
1.5X + 6Y = 1
7X + 8Y = 15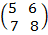
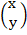 =
= 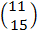
Let 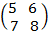 be A
be A
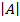 = (5×8) – (7×6)
= (5×8) – (7×6)
= 40 – 42
= -2
A-1= 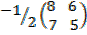
A-1 = 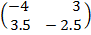
= 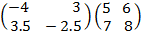
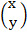 =
= 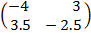
= 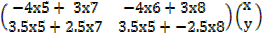 =
= 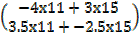
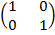
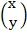 =
= 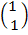
x = 1
y = 1
2.Solve the following simultaneous equation by matrix.
4X + 2Y= 40
X + 3Y = 35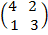
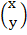 =
= 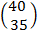
Let 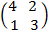 be B
be B  = (4×3 ) – ( 2×1)
= (4×3 ) – ( 2×1)
= 12 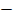 2
2
= 10
B-1= 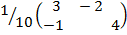
= 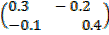
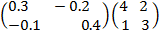
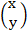 =
= 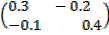
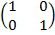
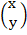 =
= 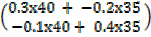
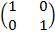
 =
=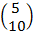
X = 5
Y = 10
CRAMMERS RULE FOR SOLVING SIMULTANEOUS EQUATIONS
Is a rule used to solve the simultaneous equations
Consider the following examples
Solve the following system of simultaneous equation
1. 5X+6Y = 11
7X + 8Y = 15
Solution
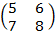
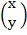 =
= 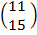
Let A = 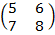
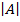 = ( 5×8) – (7×6)
= ( 5×8) – (7×6)
= 40-42
= -2
Let B = 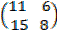
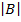 = (11×8) – (15×6)
= (11×8) – (15×6)
= 88- 90
= -2
X= 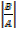 =
= 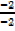 = 1
= 1
X= 1
Let C = 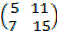
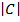 = ( 5×15) – (7×11)
= ( 5×15) – (7×11)
= 75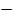 77
77
= -2
Y = 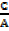 =
= 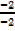
2. 4X-6= -3Y
4+5Y = -2X
Solution
4X+ 3Y = 6
-2X-5Y = 4
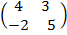
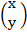 =
= 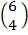
Let A = 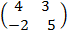
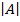 = (4X-5) – (-2X3)
= (4X-5) – (-2X3)
= -20 + 6
= 14
Let B = 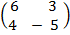
A = (4X-5) – (-2X3)
Let B = 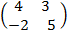
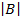 =(6X-5) – (4X3)
=(6X-5) – (4X3)
= -30 -12
= -42
X= 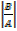 =
= 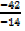 = 3
= 3
X= 3
Let C = 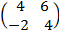
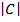 = (4X4) – (-2X6)
= (4X4) – (-2X6)
= 16- -12
= 28
Y = 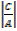
Y = 28
-14
Y = -2
TRANSFORMATION IN THE PLANE
Transformation in the plane is a mapping which shifts an object from one position to another within the same plane.
Examples of transformations in the xy plane are
i. Reflection
ii. Rotation
iii. Enlargement
iv. Translation
REFLECTION
-The action or process of sending back light, heat or sound from a surface.
ISOMETRIC MAPPING
-Is a transformation which the object size is maintained.
-Reflection is an example of isometric mapping.
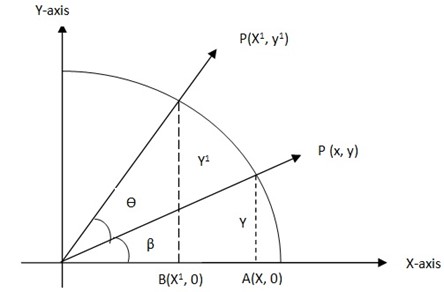
Reflection in the line included an angle (α) passing through the origin.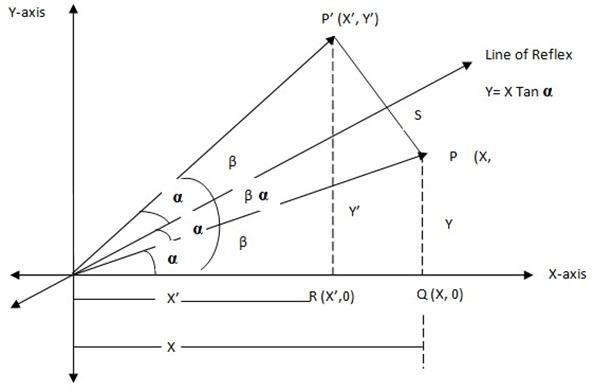
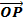 inclined at B with the coordinates being (X, Y)
inclined at B with the coordinates being (X, Y)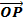 is the image of
is the image of 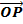 under reflection is
under reflection is 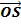
PP is perpendicular to OS (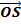 is the line of reflection)
is the line of reflection)
POS= α 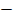 β
β
Δ OPQ is right angled at Q
Hence X = OP cos B……(i)
Y = OP sin B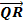 is perpendicular to the axis of X at R
is perpendicular to the axis of X at R
Coordinates of R are ( X1,0)
OR= X 1
RP1=Y1
Δ OP1R is right angled at R
P1OS= POS= α-β
Angle P1OR = α – β + α – β + β = 2α – β
Cos (2α-β)= X1
OP1
X1= OP1cos (2α-β)….. (iii)
Y1 = sin (2α-β)
OP1
Y1=OP1sin (2α-β)……(iv)
Cos (A+B) = cos A cos B – sin A sin B
Sin(A+B) = sin A cos B+ sin B cos A
X1 = OP1 cos 2α cosβ + OP sin 2α cos β…. (iii)
Y1= OP sin 2α cos β – OP1 sin B cos 2α
X1= OP cos 2α cos β+ OP sin 2α sin β
Y1= OPsin2αcos β – Op sinβ cos 2α
X1 = OP cos β cos2α + OP sin β sin 2α
Y1= OP cos βsin 2α – OP sin β cos 2α
X1 = X cos 2α + Y sin 2α …..( i)
Y1 = X sin 2α – Y cos 2 α …..(ii)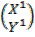 =
= 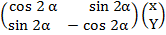
Exercise
1. Find the image of the point A (1, 2) after a reflection in the Y= X plane.
Solution;
Y= X  = 1
= 1
Tan α =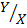 = 1
= 1
α= 900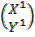 =
= 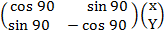
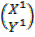 =
= 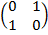
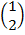
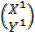 =
= 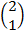
(X1, Y1) = (2, 1)
2. Find the image of B (3,4) after a reflection in the line Y= -X followed by another reflection in the line Y= 0
My = -X
My = 0
Y= -X

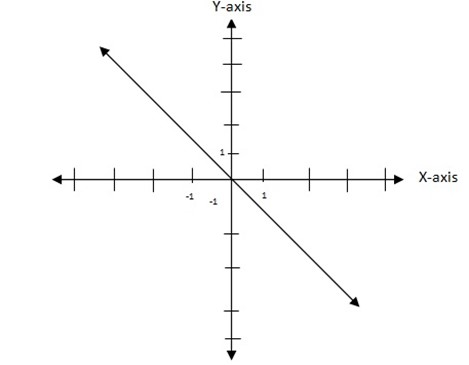
y = – x
y = – 1
x
α = – 450 for clockwise movement
Or
α = 1350 anticlockwise movement
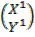 =
= 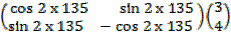
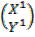 =
= 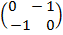
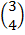
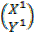 =
= 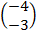
(X1, Y1) = (-4, -3)
Followed reflection at Y = 0
Tan α = 0
α = 0 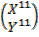 =
= 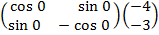
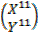 =
= 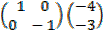
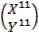 =
= 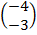
(X11, Y11) = (-4, 3)
In questions 3 to 6, write the matrix of reflection in a given line.
3. Y= 0 ( the X axis)
Y= 0
Tan α= 0
α= 0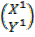 =
= 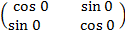
Mx = 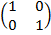
4. Y = X 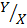 = 1
= 1
Tan α= 1
Α= 900
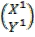 =
= 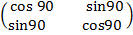
= 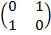
5. X = 0
Tan α = 0
α= 0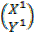 =
= 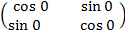
= 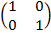
6. Find the image of the point (1, 2) after a reflection in the line Y= X followed by another reflection in the line Y= -X.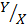 = 1
= 1
Tan α = 90 0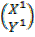 =
= 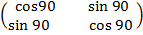
= 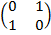
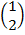
= 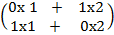
= ( 2, 1)
ROTATION
Find the image of the point B (1,2) after a rotation by 900 about the origin.
Solution: 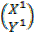 =
= 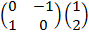 =
= 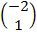
Rθ = 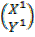 =
= 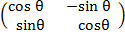
IMAGE OF A POINT ROTATED AT INCLINED LINE AT ANGLE B
Let 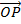 be inclined at an angle B
be inclined at an angle B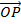 =
= 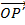
PA is perpendicular to the X – axis at A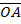 = X ,
= X , 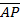 = Y
= Y
ΔOAP is right angled at A with POA = B
Cos B = X
OP
X = OP Cos B …….(i)
Sin B = Y
OP
Y = OP sin B ….. (ii) 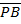 is perpendicular to the X – axis at B
is perpendicular to the X – axis at B
Cos (B+ θ) = X1
OP
X 1 = 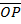 cos ( B + θ)
cos ( B + θ)
X1 = 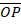 cos B cos θ – OP sin B sinθ
cos B cos θ – OP sin B sinθ
X1 = X cos θ – Y sin θ ……(iii)
Sin (B+ θ) = Y 1
OP
Y1= 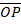 sin (B+ θ)
sin (B+ θ)
Y1= 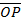 sin B cos θ +
sin B cos θ + 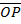 sin θ cos B
sin θ cos B
Y1= Y cos θ + X sin θ …..(iv)
In matrix form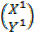 =
= 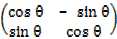
Question
The matrix of rotation
1. 900 about the origin.
R = 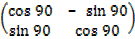
= 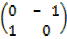
2. find the image of (1,2) after a rotation of 900 followed by another rotation of 2700 about the origin.
Solution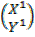 =
= 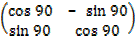
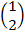
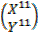 =
= 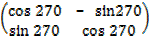
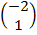
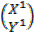 =
= 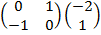
= 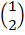
3. Find the image of 3X + 4Y + 6 = 0 under a rotation of 900 about the origin.
Solution:
3X + 4Y = -6
X intercept, Y = 0
3X = -6
X = -2
Y intercept, X = 0
4Y= -6
Y = 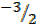
(-2,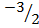 )
)
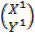 =
= 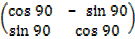
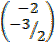
= 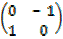
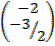
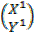 =
= 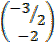
TRANSLATION
Exercise
1. A translation takes every point a distance 1 unit to the left and 2 units downwards. Find where it takes.
a. (0,0)
b. (1,1)
c. (3,7)
Solution
a. (0,0)
(a,b) = (-1,-2)
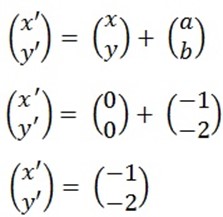
b. (1,1)
(a,b) = (-1,-2)
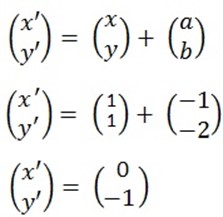
C. (3,7)
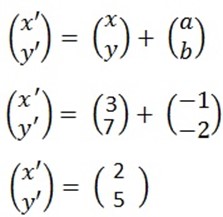
2. If translation takes the origin to (8,7). Given
U= (-12, 12) , v= (6,-16)
find T(u+v)
= ( u + v)
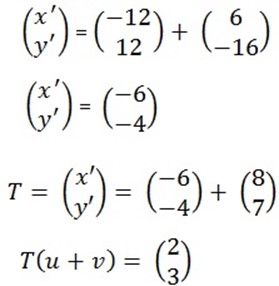
3. Find the image if the line 3x + 4Y + 6 = 0 under a translation by the vector (-6,-1)
3x + 4Y -6 = 0
Solution
Y = mx + c
4Y = -3/4 x – 3/2
X intercept, y=0
3x+ 0 + 6=0
3X= -6
X = -2
(-2,0)
Y intercept, X= 0
0 + 4Y + 6 = 0
4Y = -6
Y = 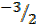
(0,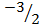 )
)
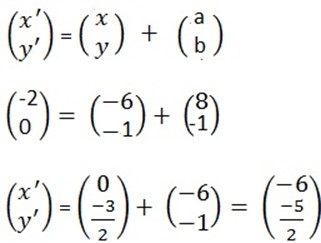
(-8,-1) and (-6,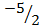 )
)
Y- Y1 = M (X-X1)
Y- -1 = M( X- -8)
Y + 1 = 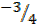 (X+8)
(X+8)
Y+1 = 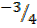 X +
X + 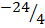
Y= 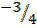 X
X 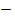 7
7
4. Find the image of the line Y = X under a translation by the vector (5,4)
Solution
Y = X
|
X |
-2 |
1 |
|
Y |
-2 |
1 |
edu.uptymez.com
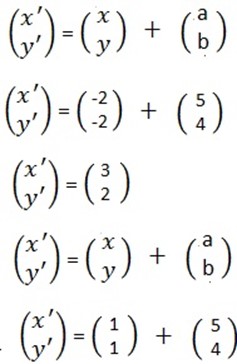
(3,2) and (6,5)
Slope = 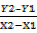
= 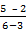
= 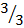
M =1 (3 ,2)
Y-Y1 = M ( X –X1)
Y-2 = 1(X – 3)
Y-2 = X – 3
Y = X – 3 + 2
Y = X -1
LINEAR TRANSFORMATIONS
Consider transformation T,
Let u and v be two vectors
Let t be the real number
The t is a linear transformation if it obeys the following properties.
i. T (tu) = t T (u)
ii. T( u+v) = T (u) + T(v)
ENLARGEMENT
The transformation which magnifies an object such that its image is proportionally increased or decreased in size by some factor.
General matrix of enlargement is 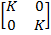
where k is non zero or real number (Linear scale factor)
EXERCISE
1. Find the image of (1,2) under the enlargement by T= 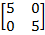
Solution 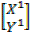 =
= 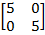
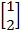 1 =
1 = 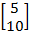
(X1, Y 1) = (5, 10)
2. Find the image of ( -1/2 , -1/3 ) under the enlargement by
T=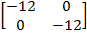
Solution 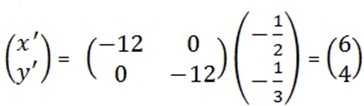
(X‘, Y ‘) = (6, 4)
3. Find the enlargement matrix which maps the point (3,-4) into (18, -24).
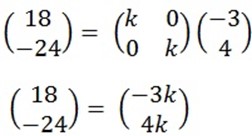
-24 = 4k
18 = -3k
K= -6
-24 = 4K
K = -6
(-6,-6)