QUADRATIC EQUATION
Is any equation which can be written in the form of ax2 + bx + c=0 where a ≠ 0 and a, b and c are real numbers.
SOLVING QUADRATIC EQUATION
i) BY FACTORIZATION
Example 1
solve x2 + 3x – 10 = 0
Solution:
x2 + 3x – 10 = 0
(x2 – 2x) + 5 (x – 2) = 0
x (x – 2) + 5 (x – 2) = 0
(x + 5) (x – 2) = 0
Now x + 5 = 0 or x – 2 = 0
x = -5 or x = 2
x = -5 or 2
Example 2
Solve for x
i) 2x2 + 9x + 10 = 0
Solution:
Sum = 9
Product = 2 x 10 = 20
20 = 1 x 20
= 2 x 10
= 4 x 5
(2x2 +4x) + (5x + 10) = 0
2x(x + 2) + 5(x + 2) = 0
(2x + 5) (x + 2) = 0
Now,
2x + 5 = or x + 2 = 0
x= -2.5 or -2
ii) 2x2 – 12x = 0
Solution:
2x(x – 6) = 0
2x = 0 or x – 6 = 0
X = 0, or x = 6
X = 0 or 6
iii) x2 – 16 = 0
Solution:
x2 – 16 = 0
(x2) – (4)2 = 0
(x + 4) (x – 4) = 0
Now, x + 4 = 0 or x – 4 = 0
x = -4 or x = 4
EXERCISE
1. Solve for x from
X2 – 7x + 12=0
Solution:
x2 – 3x – 4x + 12 = 0
(x2 – 3x) – (4x – 12) = 0
x(x – 3) – 4(x – 3) = 0
(x – 4) (x – 3) = 0
Now, x – 4 = 0 or x – 3 = 0
x= 4 or x = 3
ii) 4x2 – 20x + 25 = 0
Solution:
4x2 – 10x – 10x – 25 = 0
(4x2 – 10x) – (10x – 25) = 0
2x(2x – 5) – 5(2x – 5) = 0
(2x – 5) (2x – 5) = 0
Now, 2x – 5 = 0 or 2x – 5 = 0
x = 
iii) 4x2 – 1 = 0
Solution:
4x2 – 1 = 0
22x2 – 1 = 0
(2x)2 – (1)2 = 0
(2x + 1) (2x – 1) = 0
Now, 2x + 1 = 0, or 2x – 1 = 0
X = 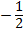 or x =
or x =
iv) (x – 1)2 – 81 = 0
Solution:
(x – 1)2 – 92 = 0
(x – 1 – 9)(x – 1 + 9) = 0
Now, x – 1 – 9 = 0, or x – 1 + 9
x – 10 = 0, x + 8 = 0
x = 10 or x = – 8
v) 2x2 = 10x
Solution:
2x2 – 10x = 0
2x(x – 5) = 0
2x = 0 or x – 5 = 0
x = 0, or x = 5
SOLVING BY COMPLETING THE SQUARE
Example 1
Solve i) 2x2 + 8x – 24 = 0
Solution:
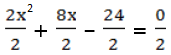
x2 + 4x – 12 = 0
x2 + 4x = 12
x2 + 2x + 2x + 4 = 12 + 4
(x2 + 2x) + (2x + 4) = 16
x(x+ 2) + 2(x +2) = 16
(x +2) (x +2) = 16
(x +2)2 = 16
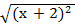 =
= 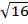
x + 2 = 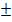 4
4
X = 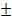 4
4 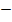 2
2
X = 2 or x =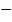 6
6
X = 2 or 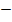 6
6
ii) x2 + 5x – 14 = 0
solution:
x2 + 5x = 14
(x2 + 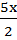 ) + (
) + (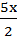 +
+ 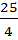 ) = 14 +
) = 14 + 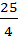
x(x +  ) +
) + (x +
(x +  ) =
) = 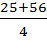
(x +  )(x +
)(x +  ) =
) = 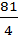
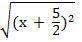 =
= 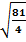
x +  =
= 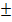

x= 
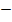
 or x =
or x = 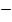

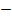

x = 2 or 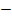 7
7
iii) 3x2 – 7x– 6 = 0
Solution:
x2 – 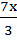 – 2 = 0
– 2 = 0
x2 – 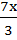 = 2
= 2
x2 – 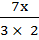 –
– 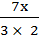 +
+ 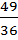 = 2 +
= 2 + 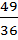
(x2 – 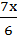 ) –(
) –( 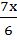 –
– 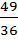 )=
)= 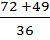
x(x –  ) –
) –  (x–
(x–  )=
)= 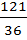
(x–  )(x–
)(x–  )=
)= 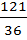
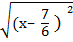 =
= 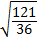
x –  =
= 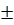
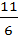
Now,
x –  =
= 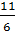 , x –
, x –  =
= 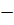
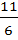
x = 3 or x = 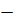

iv) x2 – 5x + 2 = 0
x2 – 5x = -2
x2 – 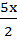 –
– 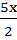 +
+ 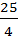 = -2 +
= -2 + 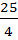
x(x –  –) –
–) –  (x –
(x –  –) =
–) = 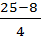
(x –  )2 =
)2 = 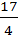
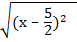 =
= 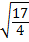
x –  = ±
= ±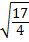
x =  ±
±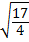
x = 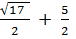 or
or 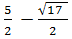
GENERAL FORMULA
1. Solve ax2 + bx + c = 0
Solution:
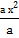
x2
+  +
+  = 0
= 0
x2
+  =
=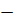

x2
+ 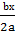 +
+ 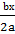 +
+ 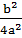 =
= 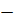
 +
+ 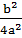
(x2
+ 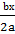 ) +(
) +( 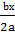 +
+ 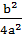 ) =
) = 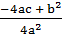
x(x + 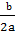 ) +
) + 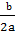 ( x +
( x + 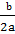 ) =
) = 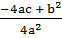
(x + 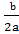 )2 =
)2 = 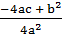
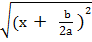 =
= 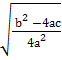
x + 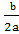 =
= 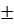
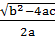
x =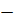
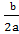
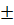
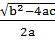
Generally, 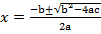
Example 1.
Solve for x by using generally formula
i) 6x2 + 11x + 3 = 0
Solution: a = 6, b = 11, c = 3
From the general equation, 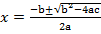
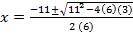
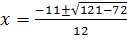
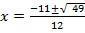
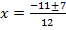
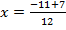 and
and 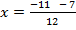
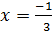 and
and 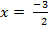
ii) 5x2 – 6x – 1 = 0
Solution:
a= 5, b = -6, c =1
From the general equation, 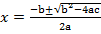
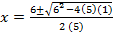
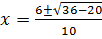
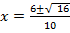
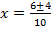
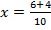 and
and 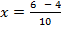
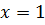 and
and 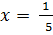
iii) 0 = 400 + 20t – t2
solution:
t2
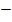 20t
20t  400 = 0
400 = 0
a = 1, b = -20, c = -400
From the general equation
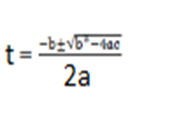
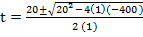
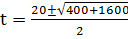
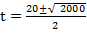
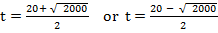
GRAPHICAL SOLUTION OF QUADRATIC EQUATION
– The general quadratic equation ax2 + bx + c =0 can be solved graphically
– First draw the graph by setting ax2 + bx + c = y and then
Drawing graphs
Example 1
Draw the graph of the following equation
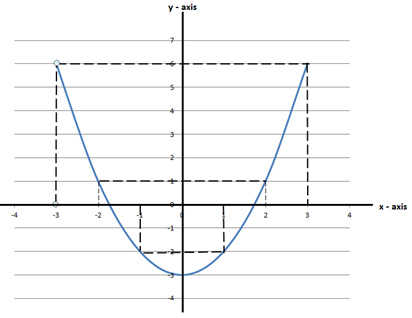
i) y = x2 – 3
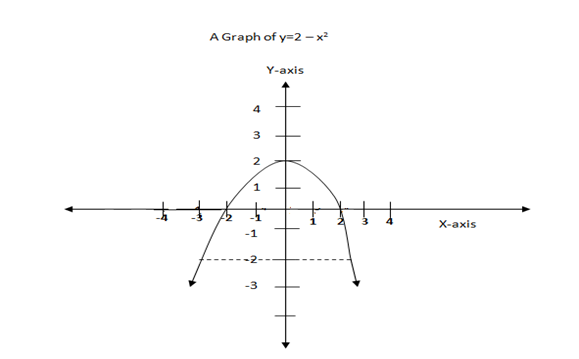
ii) y = 2 – x2
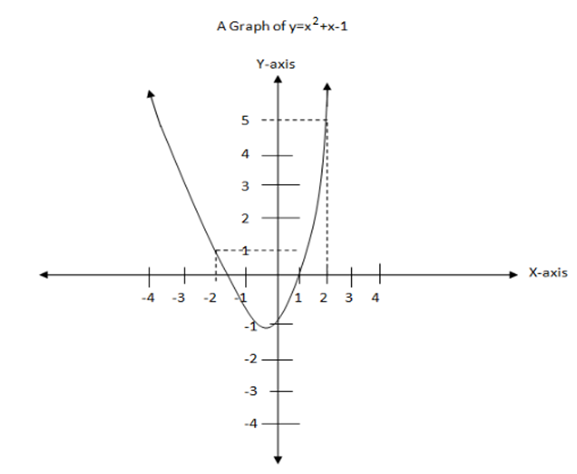
iii) y = x2 + x – 1
Solution:
i) y = x2 – 3
TABLE VALUE
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
6 |
1 |
-2 |
-3 |
-2 |
1 |
6 |
edu.uptymez.com
ii) y = 2 – x2
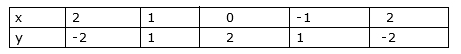
iii) y = x2 + x – 1
Solution:
APPLICATION OF GRAPHS IN SOLVING QUADRATIC EQUATION
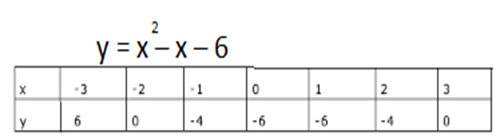
a) Solve graphically the equation x2 – x – 6 = 0
b) Use the graph in a to solve the equation
x2 – x – 2 = 0
Solution:
x2 – x – 6 = 0
Let y=x2 – x – 6…………………….(i) Then
y=0………………….(ii)
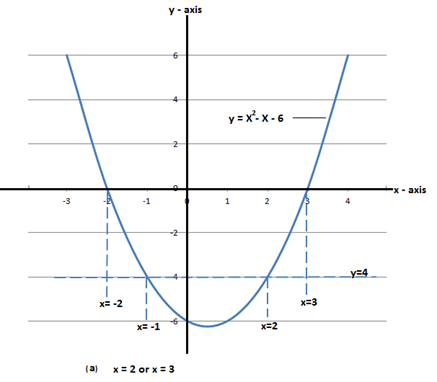
(b)From x2 – x – 6 = 0
Then
x2 – x – 2 = 0 can be written as
x2 – x –2-4 = 0-4
x2 – x – 6 = -4 But y=x2 – x – 6
∴y=-4
∴x=-1 or x=2
More examples
1. A man is 4 times as old as his son. In 4 years the product of their ages will be 520.
Find the sons present age

Now
(x + 4) (4x + 4) = 520
4x2 + 4x + 16x + 16 = 520
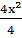 +
+ 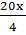 –
– 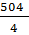 =
= 
x2 + 5x – 126 = 0
a=1, b = 5, c = -126
From the general equation, 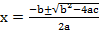
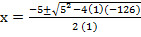
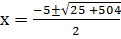
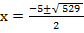
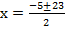
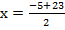 and
and 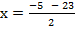
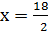 and
and 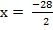
x = 9 or -14.
The present age of the son is 9
2.Find the consecutive numbers such that the sum of their squares is equal to 145
Solution:
Let x be the first number and x + 1 be the second number
Sum of x2 + (x + 1)2 = 145 their squares
Now, x2 + (x + 1)2 = 145
x2 + x2 + 2x + 1 = 145
2 x2 + 2x – 144 = 0
Divide by 2 both sides , then x2 + x – 72
a =1, b =1, c = -72
From the general equation, 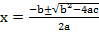
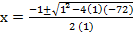
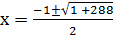
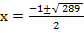
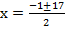
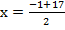 and
and 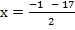
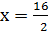 and
and 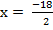
x = 8 and 9
or x = -9 and -8
The two consecutive numbers are 8 and 9 or -9 and -8.