Form 2 Mathematics – LOGARITHMS

LOGARITHMS

STANDARD NOTATIONS
Standard notation form is written in form of A x 10ⁿ whereby 1≤ A< 10 and n is any integers

Example

Write the following in standard form
(i)  2380

   Solution:
   2380 = 2.38 x 10³

(ii)  97

     Solution:
     97 = 9.7 x 10¹

(iii) 100000

       Solution:
        100000 = 1 x 10⁵

(iv)  8
        Solution:
          8 = 8 x 10⁰

Example

Write the following in standard form

(i) 0.00056
 = 5.6 x 10^-4

(ii) 0.001
 = 1 x 10^-3

(iii) 0.34
 = 3.4 x 10 ^-1

(iv) 2. 0001
 = 2. 0001 x 10⁰

EXERCISE 1:

i). Write the following in standard form

17000
     = 1.7 x 10⁴

ii) 0.00998
      = 9.98 x 10^-3

iii). Write in standard form

 0.000625
     = 6.25 x 10^-4

8/300 correct to four significant figure

8/300 =  0.02666

Now 2.667 x 10^-2

2.667 x 10^-2

iv) If a = br and  a =  8.4 x 10⁴ , b = 7.0 x 10²  Find  r.

solution:

a = 84 000

b = 700

Now

br = a

(700) (r) = 84000

  
r=120
r = 1.2 x 10²

DEFINITION OF LOGARITHMS

Consider

3 x 3 x 3 x 3 then

3 x 3 x 3 x 3 = 3⁴ =  81, the number 3 is the base ,and 4 is the exponent.

Now we say;

Logarithm of 81 to base 3 is equal to exponent 4

 log₃81 = 4
In short bⁿ = a

log_ba= n

Example 1.
Write the following in logarithmic form

i) a⁵ = 10
   log_a10 = 5

ii)10^-3 = 0.001
    10^-3= 0.001
    log₁₀0.001 =  -3

iii) 2^-1 = ½
  log₂1⁄2  = -1

iv) 3 = 9^1/2
log₃9 = 1⁄2

Example  2

Write the following in exponential form
 (i) log₃729= 6
        3⁶ = 729

 (ii) log₃1⁄3 = -1
        3^-1 = 1/3

 (iii) log₁₀0.01 = -2
       10^-2 = 0.01

  (iv)1⁄2 = log₄2
        4^(1/2) = 2

Example 3

If log₁₀0.01= y. Find y

Solution:

log₁₀0.01 = y

10^y = 0.01

10^y =1×10^-2

10^y=10⁰×10^-2

10^y=10^-2

y= -2
 

If log₁₀x=-3 find x

Solution:
log₁₀x = -3

10^-3 = x

x=0.001

EXERCISE  1
1. Write in standard form  
                    i) 405.06
                   ii) 0.912
Solution:
i) 405.06 = 4.0506 x 10²
ii) 0.912 = 9.12 x 10^-1

2. Write in logarithimic form
i)5^-1 = 1⁄5
ii) 0.0001 =1 × 10^-4

Solution:
i) 5^-1 = 1⁄5
 log₅(1⁄5) = -1

ii) 0.0001 = 10^-4
log₁₀0.0001 = -4

3. Write in exponential form
i)  log_ax = n
ii)-3 =  log₁₀0.001
iii) log₂(1⁄64) = -6

Solution:
i)  log_ax = n
 aⁿ = x

ii)-3 =log₁₀0.001
    10^-3 = 0.001

iii) log₂(1⁄64) = -6
     2^-6 = 1⁄64 

4. To solve for x
i)  log₆x= 4
     6⁴ = x
     x = 1296

ii) x = log₃6561
    3^x = 6561
    x = 8

iii) log_x10= 1
 x¹ = 10
 x = 10

 iv) log₄2 =  x
     4^x = 2
     2^2x = 2¹    
     2x= 1
     x = 1⁄2

BASE TEN LOGARITHM
– Is an logarithm of a number to base 10. Also known as common logarithm
  example    i) log₁₀5= log5
                  ii) log₁₀75 =  log75

                         iii) log₁₀p = log p

SPECIAL CASES
(1).  log_aa = x
a^x = a¹
x = 1

Generally log_aa  = 1

Example
i) log₆6  = 1
ii) log10  = 1

(2) log_a(aⁿ) = x
            a^x = aⁿ
            x = n

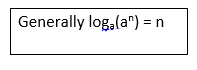
Example   i) log₄(4⁵) = 5
               ii) log10^-3  = -3

Example 1

If log₅5 = log₂m  Find m

Solution:

log₅5 = log₂m  

But log₅5 = 1

1 = log₂m

2¹ = m¹

m = 2

Example 2

Given log₅25 + log₄x = 6, Find x

Solution:

log₅25 + log₄x = 6

log₅(5²)+ log₄x = 6

2log₅5+log₄x = 6

2 +log₄x = 6

log₄x  = 4
       x= 4⁴

       x = 256

EXERCISE 2.

 Evaluate

 i) log₂4096 
                  
ii) log0.0001

solution

i) log₂4096      
              
let x = log₂4096
2^x = 4096

2^x = 2¹²

x = 12

∴log₂4096=12

ii) log0.0001

Solution:

Let x = log0.0001
10^x = 1/10000
10^x = 1/(10⁴)
10^x = 10^-4
x = -4

∴log0001=1

2) If log_k81 – log₂32= -1

Solution:
  log_k81 – 5log₂2 =  -1
 log_k81 = -1 + 5
 log_k81= 4
 k⁴ = 81
 k⁴ = 3⁴
 k = 3

3. Given log₆y = log₇343. Find y

Solution:

log₆y = 3log₇7

log₆y  = 3

6³ = y

216 = y

y = 216

4) Solve for m

i) log₈1  = m
8^m = 1         since aº=1 then
               
                   8^m=8⁰

                   m=0

ii) log₅m + log₃27 = 8
log₅m + log₃3³= 8
log₅m +3 = 8
log₅m = 5
      m= 5⁵

     m = 3125

LAWS OF LOGARITHMS

MULTIPLICATION LAW

 Suppose, log_ax = p and log_ay = q then
log_ax = p….(i)
log_ay = q….(ii)
Write equation (i) and (ii) into exponential form.
a^p = x………(iii)
a^q = y……..(iv)
Multiply equation (iii) and (iv)

xy = a^p x a^q
xy = a^{(p + q)} …….(v)

 In equation (v) apply log_a both sides
log_a (xy) = log_aa^{(p + q)}

log_axy = (p + q)  log_aa
log_axy = p + q
But p = log_ax
       q = log_ay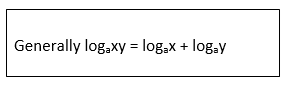

Example

 i) log₆(8 ×12) = log₈8 + log₆12
ii)  log₄9 +log₄3 = log₄(9 ×3)

Example 1

i) Find x , If log₃x = log₃15 + log₃12

Solution:

 log₃x = log₃15 + log₃12                 
  log₃x  =  log₃( 15 ×12)
  log₃x  =   log₃180 
∴ x = 180

Example 2

Given   log₅20   =   log₅4  +  log₅x .Find x

Solution:

log₅20 =  log₅4  +  log₅x

log₅20    = log₅(4 × x)   
log₅20 = log₅4x
 ∴20 = 4x
        
   X = 5

Example 3

If log₈0.01= log₈(m ×2). Find m

solution

 log₈0.01 = log₈( 2m)

   ∴ 0.01 = 2m

          m =  0.01/2

          m = 0.005

QUOTIENT LAW

Suppose, log_ax= p and
log_ay = q then
log_ax = p……..(i)
log_ay = q……..(ii) 

Write equation (i)  and  (ii) into exponent form
a^p = x……(iii)
a^q = y…..(iv)

Divide equation  (iii)  and  (iv)
x/y = a^p/a^q

x/y = a^{(p – q)} …..  (v)

In equation (v) apply log a both sides
log_a(x/y)   = log_aa^(p-q)          
log_a(x/y) = (p – q)  log_aa
But log_aa = 1
log_a(x/y) = p – q ,where p= log_ax  and q=log_ay

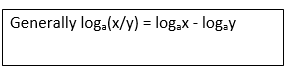
i) log₆( 8/12) = log₆8  – log₆12
ii)  log₄9   –  log₄3  = log₄(9/3)

Example

If    log₂20    =  log₂x  – log₂8.Find x

Solution:

log₂20    =  log₂x  – log₂8
log₂20     = log₂(x/8)
Now, 20 = x/8
            X = 20 x 8
            X = 160

EXERCISE 3
1. Evaluate

i) log₆3 + log₆2

Solution:

= log₆3 + log₆2

= log₆( 2 ×3)= log₆6
= 1

ii) log 40 + log 5 + log40

Solution:

= log₁₀40 + log₁₀5  + log₁₀40
= log₁₀( 40 ×5 ×40)
=log₁₀8000

iii)  log₁₀25 –  log₁₀9  + log₁₀360

Solution:

log₁₀25 –  log₁₀9  + log₁₀360
log₁₀( (25 ×360 )/9)             
              =log₁₀1000
             =log₁₀10³ 
            =3log₁₀10
            =3

2. If log_5a⁡x =  log_5a⁡9  + log_5a⁡12. Find x

Solution:

log_5a⁡x = log_5a⁡9  + log_5⁡a12
 log_5a⁡x =  log_5a⁡( 9 ×12)
log_5a⁡x = log_5a⁡108
      x = 108

3. If log_2a⁡5  = log_2ay  + log_2a⁡0.001.Find Y

Solution:

i) log_2a⁡5 = log_2a⁡(y×0.001)

5⁡ = ⁡0.001y    
  
y= 5/0.001

  Y = 5000

ii)Find y if log₆⁡100  = log₆⁡5  + log_6⁡80 – log₆⁡y

Solution:

log₆⁡100  = log₆ (5 × 80)/ y

     100 = ⁡400/y

      y   = 4

4. If   log a  = 0.9031, log b = 1.0792 and log c = 0.6990. Find log⁡ ac⁄b
 
Solution

log ⁡ac⁄b =log_10⁡ a  + log₁₀⁡c  – log₁₀⁡b
           =0.9031   + 1.0792  -0.6990

       ∴ log ⁡ac⁄b = 1.2833

LOGARITHM OF POWER

If  log_a⁡x   = p then
X = a^p
Multiply by power in both sides xⁿ = a^np

Apply log _a both sides
log_axⁿ = log_aa^np
log_axⁿ = np

But p = log_ax

∴ log_axⁿ= nlog_ax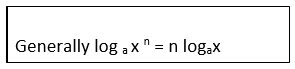

Example(1)

Evaluate

 i) log₂ (128)⁶
ii) log₇ (343)⁸

Solution
i) log₂ (128)⁶ = 6log₂ 2⁷
                
                      = (7 x 6) log₂2

                      = 42 x 1

                      = 42

ii) Log₇ (343)⁸
Solution:
      log₇ 343⁸ = 8log₇ 343
                   = 8log₇ 7³
                    = (8 x 3) log₇ 7
                   = 24

Example (2)

If log₅ 625^y = log₃ 729² .Find y.

Solution:
log₅ 625^y = log₃ 729²
log₅ 625^y = 2log₃ 729
ylog₅ 5⁴ = 2log₃ 3⁶
(y x 4) log₅ 5 = (2 x 6) log₃ 3
 4y log₅ 5 = 12 log₃ 3
          4y = 12

         y=2/4

         y = 3

LOGARITHM OF ROOTS

 

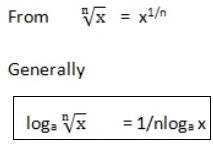
Example (1)

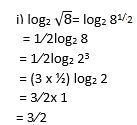
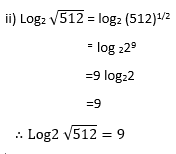
EXERCISE 4:

1. Evaluate

i) log 60 + log 40 – log 0.3
ii) log₃  √(1⁄27)

Solution:
i) Log60 + log40 – log0.3
 log₁₀ 60 + log₁₀ 40 – log₁₀ 0.3
log₁₀ (60 x 40/0.3) = log₁₀ (2400/0.3)
                          = log₁₀ 8000
                           =3.9031

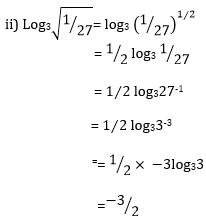
3. Given log₂ x = 1 – log₂ 3.   Find x
Solution:

log₂ x = 1 – log₂ 3
log₂ x = log₂ 2-log₂ 3
log₂ x = log₂ (2/3)
x =2/3

4. Simplify

i) 2log5 + log36 – log9
ii)  (log⁡8-log⁡4)/(log 4-log2)           
 
Solution:

i) 2log5 + log36 – log9

 log5² + log36 – log9

 log₁₀25 + log₁₀36 – log₁₀9

= log₁₀ (25 x 36)/9   
        
= log₁₀ (900/9)

= log₁₀100

=log₁₀ 10²

=2 log₁₀ 10

=2

ii) (log⁡8-log⁡4)/(log 4-log2)

Solution:

(log⁡8-log⁡4)/(log 4-log2)
  
=  log₁₀ (8/4) ÷log₁₀ (4/2)

= log₁₀2 ÷ log₁₀2
= 1