-A transformation changes the position, size, direction or shape of objects.
-Transformation in a plane is a mapping which moves an object from one position to another within the plane. The new position after a
transformation is called an image
Examples of transformations are
1. Reflection
2. Rotation
3. Enlargement and
4. Translation
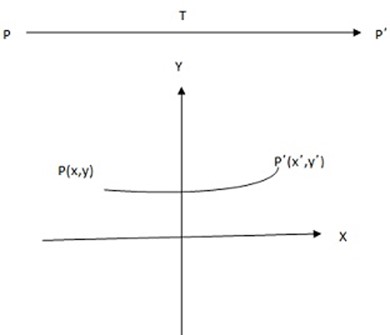
Suppose a point p[x, y] in the xy plane moves to a point pΔ [xΔ, yΔ] by a transformation T
P is said to be mapped to PΔ by T and may be indicated as
A transformation in which the size of the image is equal to the size of the object is called an Isometric mapping
REFLECTION
-Reflection is an example of an isometric mapping
-Isometric mapping means the distance from the mirror to an object is the same as that from the mirror to the image.
-The plane mirror is the line of symmetry between the object and the image.
-The line joining the object and the image is perpendicular to the mirror.
NOTE
-The symbol/letter for reflection is M.
-The reflection in X- axis and Y- axis are indicated as Mx and My respectively.
-The reflections in lines with certain equations are indicated with their equations as subscripts
For example: My = x,is given by My = –x
A) Reflection in the x-axis
Example
1. 1. Find the image of the point A(2,1) after a reflection in the x-axis
Solution:
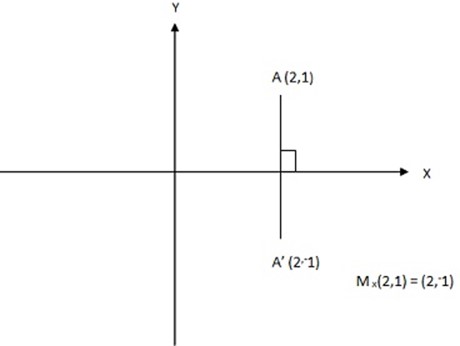
2
(B)Reflection in y-axis
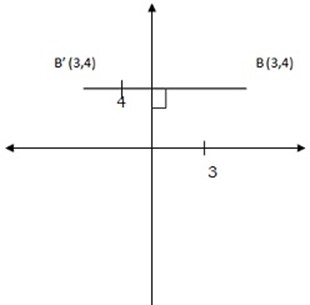
2. Find the image of 0(3,4) under the reflection in the Y-axis
Solution:
Exercise 1
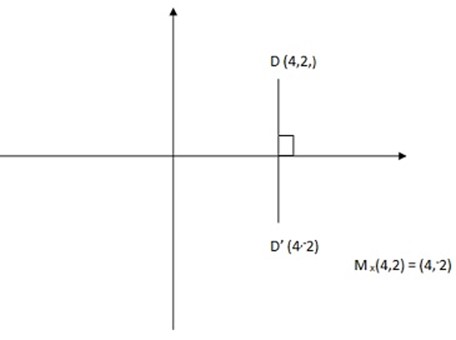
1. Find the image of the point D(4,2) under a reflection in the x-axis
Solution:
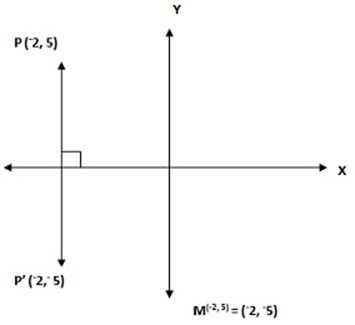
2.Find the image of the point P(-2,5) under the reflection in the x-axis
Solution:
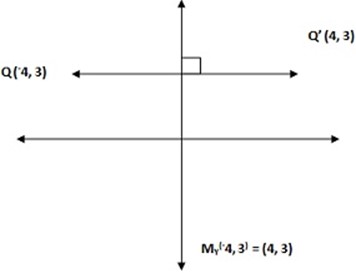
3. Point Q (-4,3) is reflected in the Y- axis
Solution:
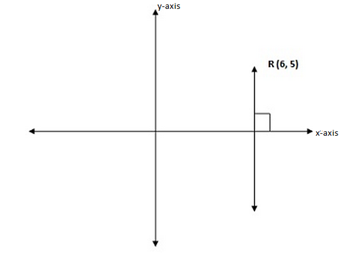
4. Point R (6, 5) is reflected in the X-axis.
Find the coordinates of its image
5. The vertices of a triangle PQR are P (6, 2), Q (–2, 8), R (–5, –1). If triangle PQR is reflected in the Y axis, find coordinates of the vertices of its image.
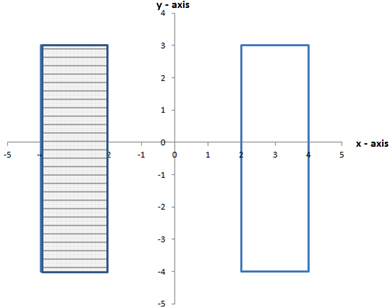
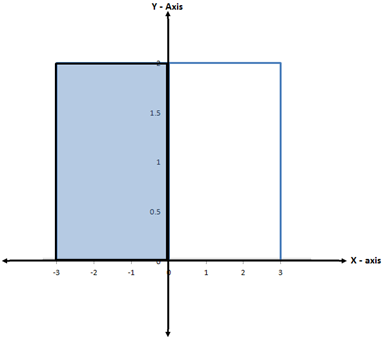
6. The vertices of rectangle area A (2,3), B (2,-4), C (4, -4), D (4,3) rectangle ABCD is reflected in the Y-axis
(a) Find the coordinates of the vertices of its image
(b) Draw a sketch to show the image
Solution
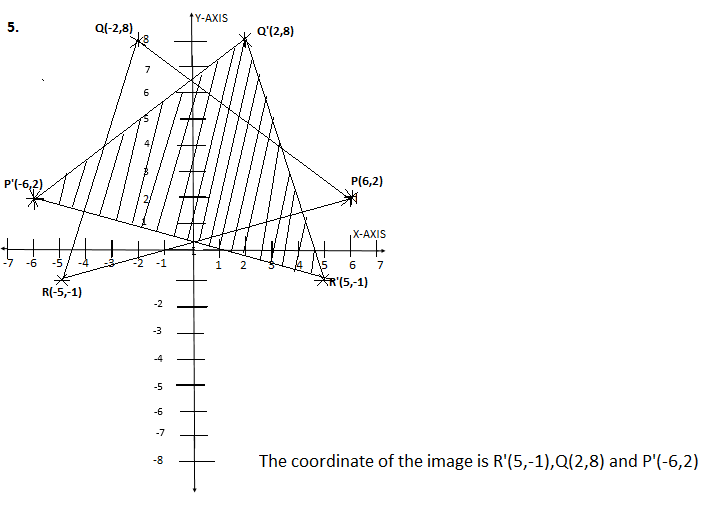
6(a)The coordinate of the image is A'(-2,3), B'(-2,-4). C'(-4,-4) and D'(-4,3)
C) THE REFLECTION IN THE LINE Y = X
The line y = x makes an angle 45º with the x and y axes
See the diagram
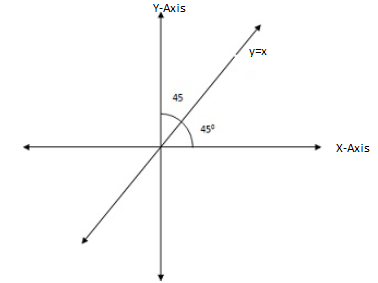
∴My=x (x,y)=(y,x)
Example
1. Find the image of point A(1,2) after a reflection in the line y=x
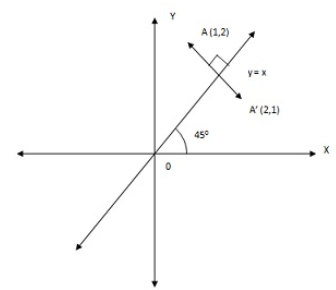
D) REFLECTION IN THE LINE Y = -X
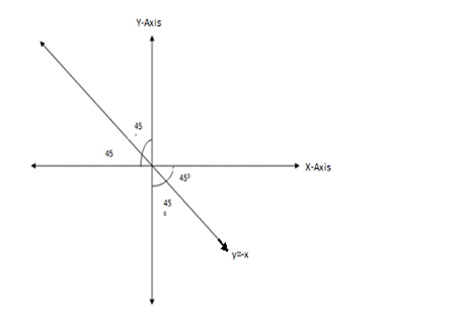
∴ My=-x(X,Y)=(-y,-x)
Example
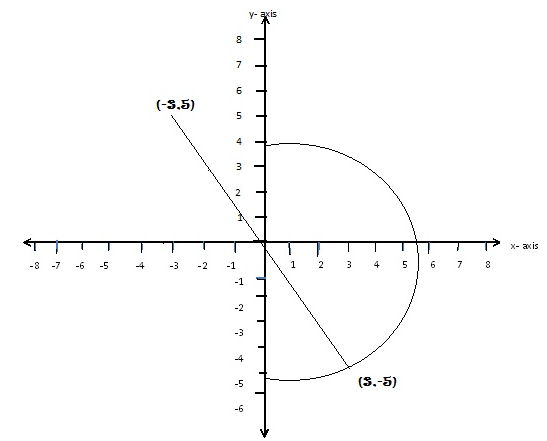
Find the image of B (-3, 4) after a reflection in the line y=-x followed by another reflection in the line y=0
Solution
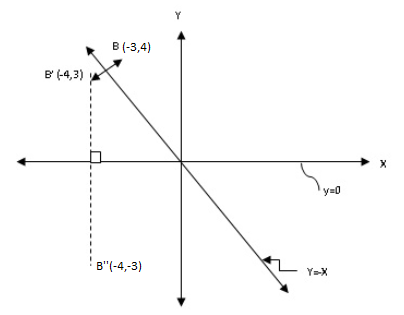
The reflection of B (–3, 4) in the line y = –x is B’ (–4, 3) and the image of
B’ (–4, 3) after reflection in the line y = 0 is B’ (–4, –3)
NOTE:
If P is the object the reflection of point P(x,y) will be:
1. M x-axis P (x,y) = P′ (x, -y)
2. M y-axis P (x,y) = P′ (-x, y)
3. M Y=x P (x,y) = P′ (y,x)
4.M y=-x P (x,y) = P′ (-y, -x)
Rotation
– -Rotation is a transformation which moves a point through a given angle.
-The angle turned through can be either in clockwise or anticlockwise direction.
– –Rotation is an isometric mapping and usually denoted as R. Rθ means a rotation through an angle θ
– -In the XY plane when θ is measured in the clockwise direction, the angle is -ve and when measured anticlockwise direction the angle is +ve
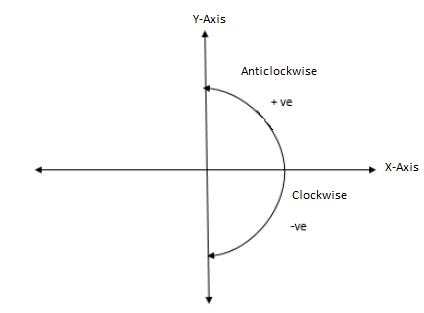
Example
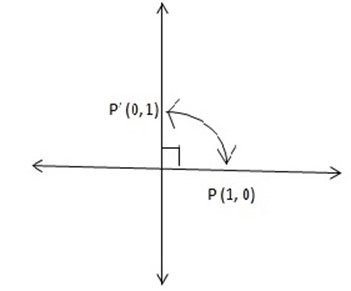
1. Find the image of the point P(1,0) after a rotation through 900 about the origin in anti-clockwise direction
TRANSLATION
– –Translation is a straight movement without turning.
– -A translation is usually denoted by T. For example T(1,1) = (6,1) means that the point (1,1) has been moved to (6, 1) by a translation T.
– – This translation will move the origin (0,0) to (5,0) and it is written as T = (5/0).
–
Examples:
1. A translation takes the origin to (–2, –5) find when it takes (–2, –3)
Solution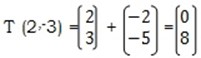
T (2,–3) = (0, –8)
2. Find the image of the point (1,2) under a rotation through 1800 anti-clockwise about the origin
Solution
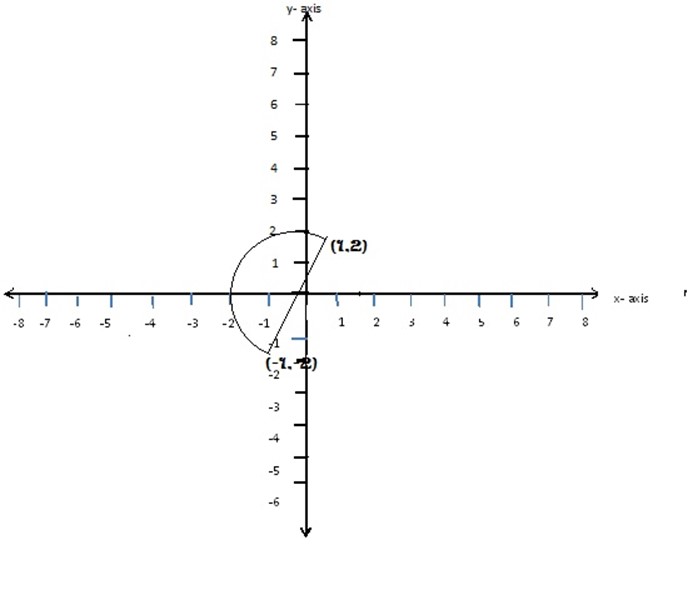
3. Find the rotation of the point (6, 0) under a rotation through 900 clockwise about the origin
Solution
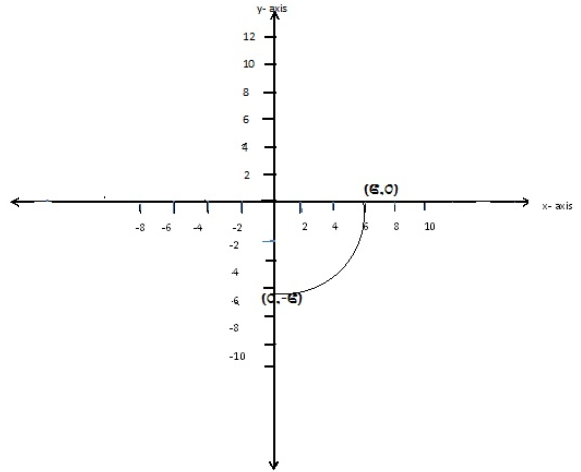
4. Find the image of (1,2) after a rotation of –900 ant –clock wise
Solution
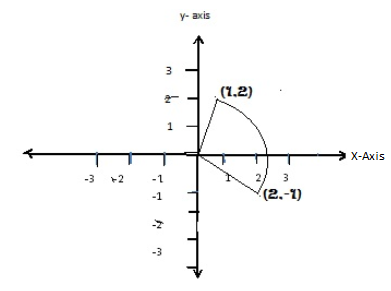
5. Find the image of (–3, 5) after a rotation of –1800
Solution
6. The vertices of rectangle PQRS are P(0,0), Q (3,0), R (3,2), S (0, 2). The rectangle is rotated through 900 clockwise about the origin.
(a) Find the co-ordinates of its image
(b) Draw the image
More examples on translation
1. Translation takes the origin to (-2, 5)
Find where it takes
(a) (-6, 6)
(b) (5, 4 )
Solution
(a)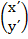 
= 
= 
= 
= 
= 
= 
+ 
= 
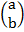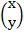
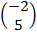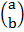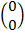
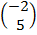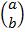
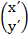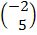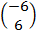
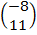
: The translation takes (-6,6) to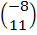
(b)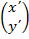 
= 
+ 
= 
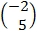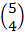
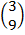
: The translation takes (5,4) to (3,9)
2. A translation takes every point a distance of 1 unit to the left and 2 units downwards on the xy-plane.
Find where it takes
(a) (0,0)
(b) (1,1)
(c) (3,7)
Solution
(a).
= 
+ 
= 
+ 
=
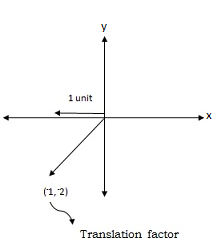
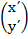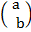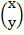
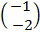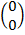
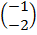
: . The translation takes the origin to (–1, –2)
(b).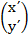 
= 
+ 
= 
+ 
=
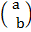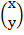
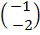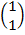
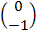
3. 3. A translation moves the origin a distance 2 units along the line y= x upwards.
Find where it takes
(a) (0,0)
(b) (2, –1)
(c) (1, 1)
Solution
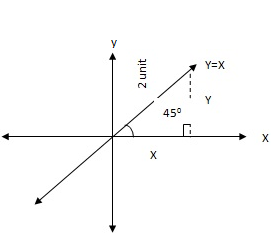
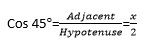
x = 2cos 450 = 2 x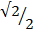 
= 
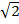
Sin 450 =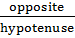 
= 
y = 2sin 450 = 2 x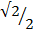 
= 
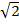
Translation factor (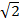
, 
)
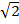(a).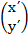 
= 
+ 
= 
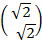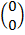
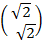
: . The origin is translated to (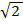 
, 
)
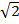(b).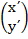 
= 
+ 
= 
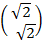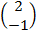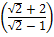
: . (2, –1) is translated to ( (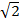
+ 2), (
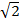– 1))
4. A translation takes the point
(3, 2) to (-4, -5), Find where it takes
(0 , 0)
Solution
= 
+ 
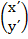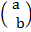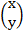where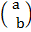 
is translation factor
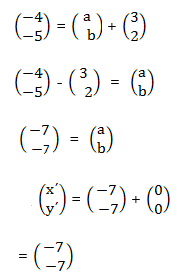
ENLARGEMENT
Enlargement is a transformation in which a figure is made larger (magnified) or made smaller (diminished).
– The number that magnifies or diminishes a figure is called the enlargement factor usually denoted by letter K. If K is less than 1 the figure is diminished and if it is greater than 1 the figure is enlarged K times.
– In case of closed figures if the lengths are enlarged by a factor K then the area is enlarged by K2
Examples: –
1. Draw a triangle PQR with vertices P (0,0), Q (0, 3) and R (3, 0)
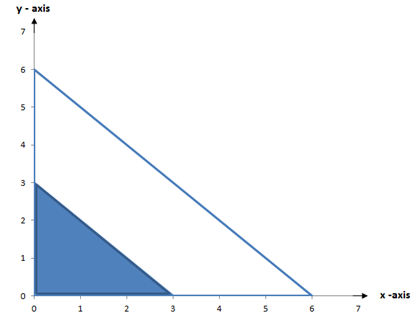
P’ = 2 (0,0) = (0,0)
Q’ = 2 (0,3) = (0,6)
R’ = 2 (3,0) = (6,0)
2. From the above question, what is the area of the new (enlarged) triangle?
Solution.
Area of the original triangle
= 
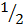x 3 x 3
= 4.5 square units
The area of the new triangle = 4.5 x K2
= 4.5 x 22
= 18 square units
3. The line segment AB with coordinated A (4,0) and B (0,3) enlarge to AΔBΔ by a factor 2. Find the coordinates for AΔ and BΔ
A’ = 2 (4, 0)
= (8,0)
B’=2(0,3)
=(0,6)
4. Find the image of the circle of radius one unit having its centre at (1,1) under enlargement transformation factor 5
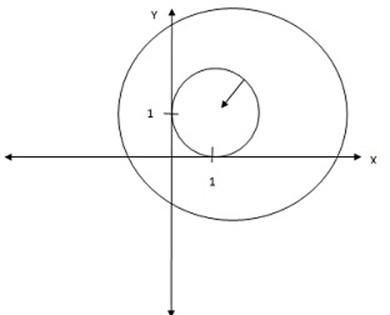
Solution:
= 5(1,1)
= (5,5)
The image of the enlarged circle is (5,5)
5.
EXERCISE 2
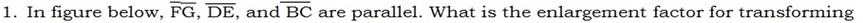
(a) Δ ADE to Δ ABC?
(b) Δ ADE to Δ AFG?
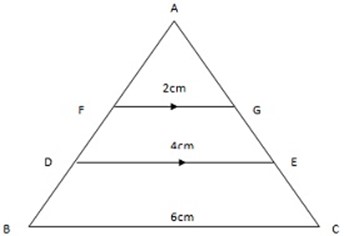
(a) Δ ADE to Δ ABC =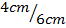
= 
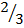
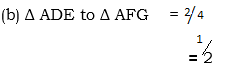
2.The point P(6,2) is enlarged by factor of 4, what is the new end point?
Solution
4 (6,2)
= (24, 8)
:. The point is (24, 8)
2. ABCD is a parallelogram
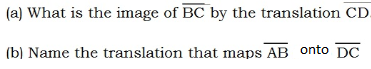
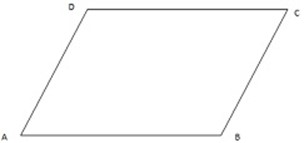
Solution
EXERCISE 3
1. List 3 examples of isometric transformation
o Translation
o Rotation
o Reflection
2. Is enlargement an Isometric transformation?
Enlargement is not an Isometric transformation.
3.Find the image of the point Q (6, –8) after a rotation of 900 about the
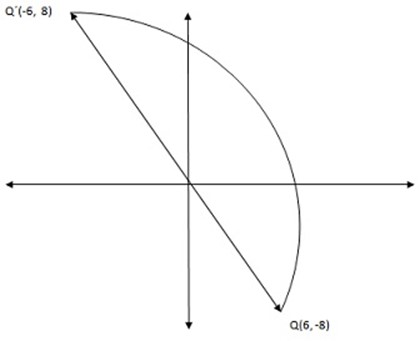
R90º(6, –8) = (–6,8)
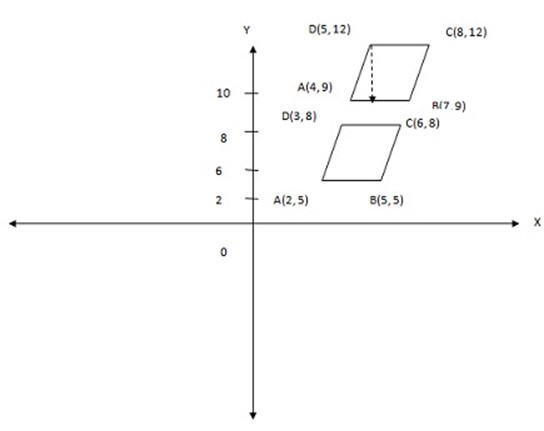
Draw a parallelogram ABCD with vertices A (2,5), B (5,5) , C (6,8), D (3,8) find and draw the image parallelogram formed by the translation wich moves the origin to (2,4)
Solution
A =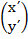 
= 
+ 
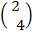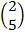
A =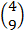 
A = (4,9)
B =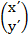 
= 
+ 
=
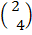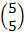
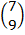
B = (7, 9)
C =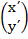 
= 
+ 
= 
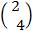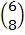
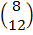
C = (8, 12)
D =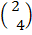 
+ 
= 
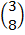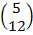
D = (5, 12)
