Form 2 Mathematics – STATISTICS

Definition

-is a branch of mathematics dealing with the study of method of collecting, organizing, analyzing, presenting and nglish-swahili/interpreting” target=”_blank”>interpreting numerical details to reach conclusions.  

Frequency nglish-swahili/distribution” target=”_blank”>distribution

Is a number of times each data point

Example 1

1.       Make  a frequency table from  the following data from the followings data  of ages 10 students 

14, 15, 16. 14, 17, 15, 16, 13,

  

2.       In mathematics test the following marks were obtained;

48 , 47,42, 67, 73, 50, 76 ,47, 44, 44, 57, 58, 54, 45, 58, 56 , 66, 67, 45, 43, 71, 48, 64, 52, 42, 54, 62, 32, 49, 34, 35, 46, 89, 37, 47, 54, 45, 60, 64, 44,.

If the class size of the class interval is 8 group the works starting with the interval 32-39 and draw the frequency nglish-swahili/distribution” target=”_blank”>distribution table.

solution

 
 

 
 

 
 

                                                                                                                            
 

 
 

 
 

 
 

 
 

 

Example

From example below find the class mark  of  the class interval 88 – 95 and 80 – 87

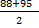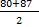
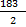class mark:      and    

                        and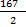   

                   =  91.5 and  83.5

Class limit ; example in class interval  88 – 95

88 is the class lower limit

95 is the class upper limit

CLASS REAL  LIMITS

class lower real limit – is the number obtained by subtracting 0.5 from a class lower limit e.g. 88-0.5= 87.5

class upper real limit obtained by adding 0.5 to the upper class limit eg, 95 + 0.5 = 95.5

class size-  is the value obtained by the difference between  the upper real limit and the  lower real limit

example .

from class interval 88-95 and 31-35

find the class size

solution:

Lower class real limit = 88 – 0.5 = 87.5

Upper class real limit = 95+ 0.5 = 95.5

Class size = 95.5 – 87.5 = 8

Lower class real limit = 31 – 0.5 = 30.5

Upper class real limit = 35+ 0.5 = 35.5

Class size = 35.5– 30.5= 5

Exercise 1: 

(1).In biology class test the following marks when obtained;

54,54,40,55,54,43,73,34, 75, 47, 35, 45,73,46,31,43,47,35,35,60,67,51,44,48,55,45,50,37,51,36

By grouping the marks in class interval 20-29 ,30-39, 40-49, etc construct the  the frequency   

Solution:                      
                                             
                                                                        DISTRIBUTION TABLE

 
 

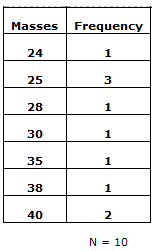
(2) The following data represent the masses of 10 people in kg. Construct the frequency nglish-swahili/distribution” target=”_blank”>distribution table for these people

30 25 35 28 38 40 25 25 40 24

 
 

Solution:                               

                                         
 

(3). The following is a set  of marks on a geography examination presents the frequency nglish-swahili/distribution” target=”_blank”>distribution table with class intervals, real limit, class marks, interval  size starting with the interval 8-15 at the bottom

Solution:
               

 
 

(4). Fill in the blank columns

Distribution of 100 math s examination score

                           
 

                                                                                                                          
 

Note:

Class real limits are also known as class boundaries
 

GRAPHS OF FREQUENCY DISTRIBUTIONS:

HISTOGRAMS

Histograms  of frequency nglish-swahili/distribution” target=”_blank”>distribution  are rectangular figures plotted with class marks against frequency . The width of the histogram equal to the class size.

Example:               

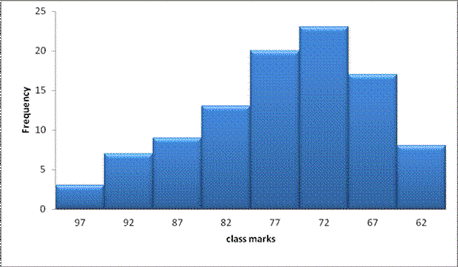
1. Draw a histogram of 100 mathematics examination scores in the table below

 
 

 
 

 
 

                                                              

 
 

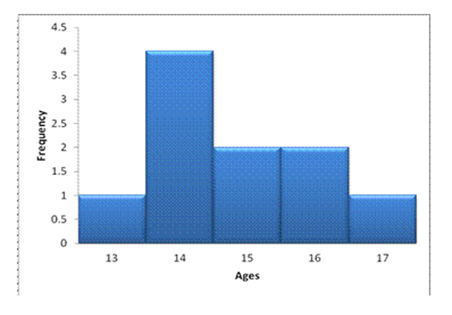
3.       . 2. Use the following nglish-swahili/distribution” target=”_blank”>distribution table below to draw a histogram

 
 

                                                                                                                                                                                                                                      
 

 
 

 
 

 
 

 
 

Solution

 
 

FREQUENCY POLYGON

Is the line graph of class frequency plotted against class marks

Steps ;

1.     1. Add one interval below the lowest interval and one above the highest interval and assign them as  zero frequency.

2.     2.  Plot a point and join them by straight lines

Example

1. Draw a frequency polygon from the following data.

                                            
 

 
 

 
 

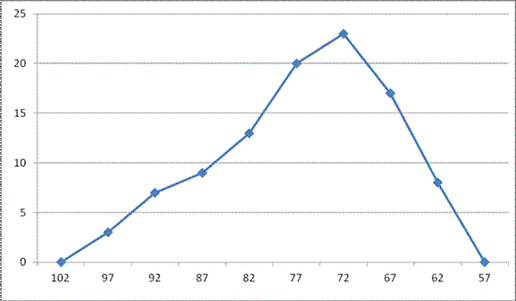
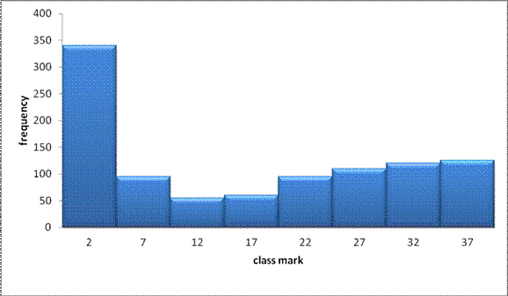
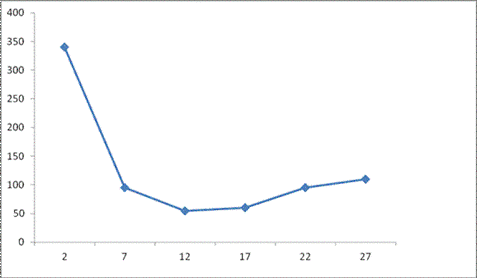
EXERCISE

1. The following table shows female death between 0 and 34 years to the nearest numbers represent  this information by

A) Histogram

B) Frequency polygon

Expected death of female per 100 women

Solution:

A) Histogram

 
 

B) FREQUENCY POLYGON             

 
 

 
 

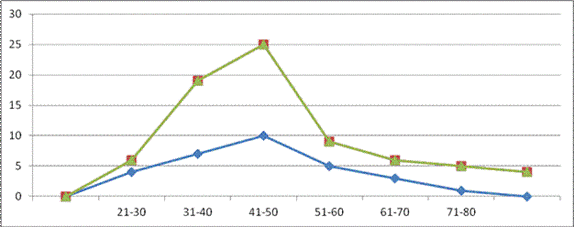
2. Table below show the nglish-swahili/distribution” target=”_blank”>distribution of marks obtained by 110 students in two different monthly tests. Draw the frequency  polygon on the same chart

 
 

                                                       
 

CUMULATIVE FREQUENCY CURVE (ORGIVE)                                                                                                                                                                     

– Cumulative frequency is the sum of all the frequency less than or equal  to a given  mark or class interval

– To calculate the cumulative frequency start with the smaller upper real limit

– Add the frequency of the smallest interval to the next interval downwards or up wards depending on whether  the data is arranged in descending or  
   ascending order 

Note:  The last entry in the cumulative frequency  is always equal to the total  number of observations 
 
– Plot upper real limit against class marks.

– Join adjacent points by a free hand.

 
 

EXAMPLES

1. Draw an  orgive for  the scores data below.

 
 

 

 

 

 

Solution; 
THE CUMULATIVE FREQUENCY DISTRIBUTION,

                                                                                                                                        N =90

 
 

 
 

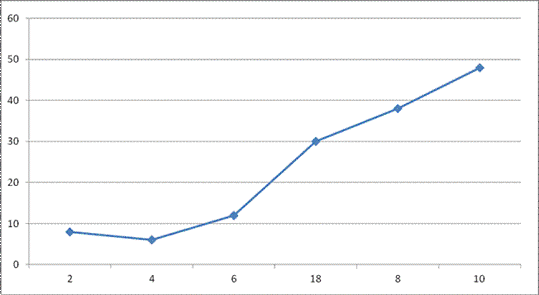
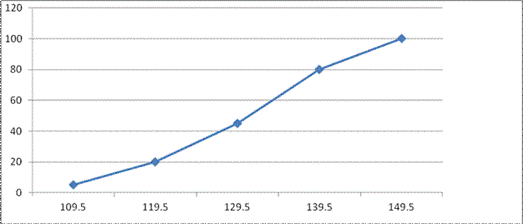
2. Motor vehicle company tested 100 cars to see how far they could travel on 10 litres of petrol. Draw the cumulative frequency curve for this company

 
 

 
 

 
 

 
 

 
 

solution

 
 

 
 

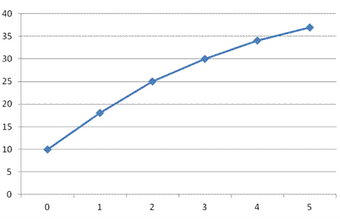
3. Platform in each square metre of a lawn were counted and recorded as follows. Draw an orgive for the platform

 
 

   

REVISION EXERCISE

1.       1.  The ages of the 22 players in a football match were  recorded in the following

      17 18 15 16 16 16 18 15 18 15 15 18 18 15 16 17 15 16 17 15 15 16 15 18 15

      Express the data in a frequency table.

        Solution:

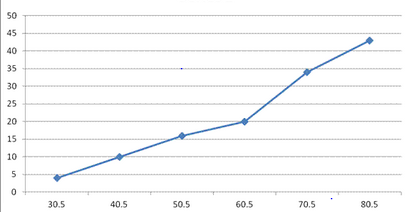
 2.        2.   The examination marks of 45 students are,

       65 58 71 62 64 35 72 32 64 46 59 82 73 76 64 63 75 71 61 36 64 80 61 64 76 64 60 68 48 35 92 73 46 24 35 43 30 50 70 40 46 64 24 28

     
       A)Make a frequency nglish-swahili/distribution” target=”_blank”>distribution using class interval 21-30, 31-40, 41-50,

         Solution:

 
 

B) Draw cumulative frequency curve

 Solution:

 

 
 

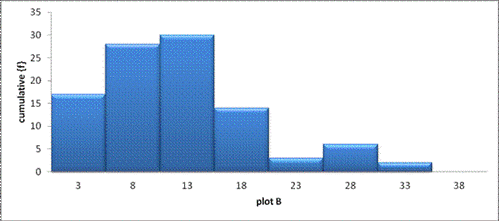
3.       3.  Two plot A and B were treated with different   families. The frequency number of potatoes on on samples of 100 plants on each plot are shown below

 

 Draw a histogram for plot B. 

  Plot B

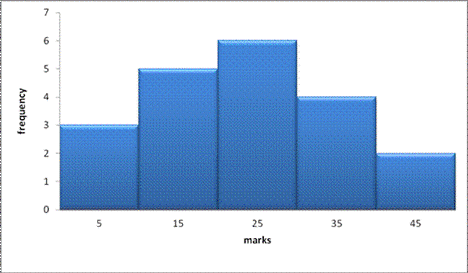
   4. In a certain examination the result were as follows;

3 student got marks between 0and 10

5 students got marks between 10 and 15

6 students got marks between 20 and 40

4 students got marks between 30 and 40

2 students got marks between 40 and 50

 Construct a histogram

                          
 

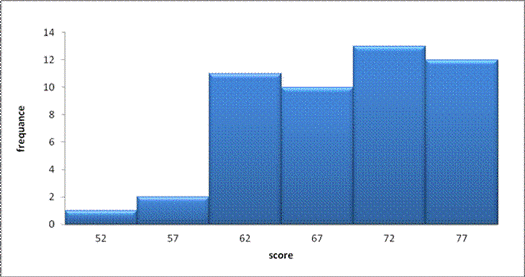
5] final score of history examination were recorded as shown in table below

 
 

A) What is the size of class intervals?
  
  Solution:

 5 is the size of class intervals  .

B)Draw a histogram to represent the scores .

 
   Solution: