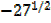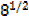BAM FORM 5 – FUNCTIONS

BASIC CONCEPTS

RELATION

Is a set of ordered pairs.

R =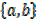     

Examples

1) Which of the following ordered pairs belong to the relation

            R ={ (x,y ) : y > x}

          ( 1,2), ( 2,1),  (-3,4),  ( -3,-5),  ( 2,2),  ( -8,0),  ( -8,-3)

       Solution

               {(1,2), (3,4), (-8,0), (-8,-3)}

2) Give 5 ordered pairs which satisfies the relation

       R =  { (x,y):y=2x}

      Solution

(1,2)(2,4)

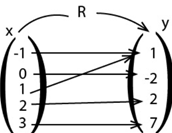
Pictorial representation of a relation

   If A= 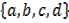  and B = 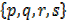then the relation between A and B

   can be represented as follows.

                                                                                                        

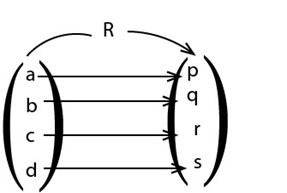
 Note

  We say that elements of a set A mapped into set B i.e

A              B

Examples

Given that A = 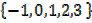    draw a pictorial representation of the relation

                                                                                                                                                      

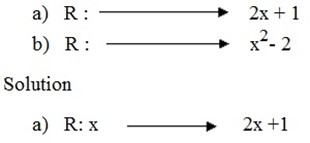
b)     R ; x     →     x² – 2

                                         

Domain and range of a relation

If R is the set of all ordered pairs [x, y] then;

Domain: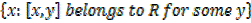    

Range     :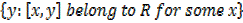 

Examples

1)     (1) Let R =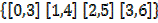   

    What is the domain and range of R?

    Solution

    Domain = 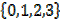   all values of x

    Range  =    all values of y

2)   (2) If R = { 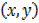: x are real numbers  and y = x² + 1}

    Find all selected pairs which belong to R when the domain is

      

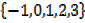
   Solution

   R =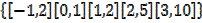  

3)  ( 3)Find the domain and range of a relation y = 2x²-1

     Solution

     Domain =   

     Range of y =2x²-1

      2x² = y + 1

 

  

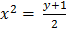
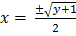
y +1  0

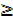y -1

 

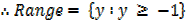
Exercise

       1)   If R = 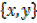   : x and y are real number  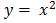 find

a)              a)   A set of ordered pairs belonging to R where domain is

           

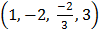
            b)     A set of ordered pairs in R  where range is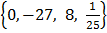   

       2.)   Let R = 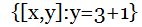     find

a)      The set of ordered pairs which belongs to R from the following

 

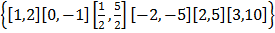
b)      The domain obtained from a

c)      The set of range obtained from a

Solution

 =  

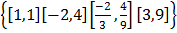
Solution

=  

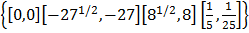
Solution

( ,) ( -2,-5) ( 3, 10)

c)    Domain = { , -2, 3 }

d)   Range = { , -5, 10}