Sub topics
-Differentiation by first principles
-Techniques of differentiation
-First and second derivatives
-Implicit differentiation
-Application of differentiation
DIFFERENTIATION BY FIRST PRINCIPLE
The concept of differentiation
The gradient of a curve at a given point is defined as the gradient of the tangent to the curve at that point and is given by the change of y with respect to x.

As B  A
A
The gradient of the chord AB
The gradient of a tangent AT at point A
Or
Line gradient of chord AB = gradient of tangent AT
Example
Find the gradient of the curve
y = 2x2+ 5
Solution
At point Q
y + 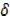 y = 2 [x+
y = 2 [x+ 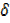 x]2 +5
x]2 +5
=2 [x2+ 2x 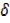 x+
x+ 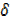 x2] +5
x2] +5
= 2x2 +4x 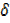 x + 2
x + 2 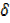 x2 +5…………. (i)
x2 +5…………. (i)
Subtracting y from equation (i)
y + 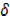 y –y = 2x2 + 4x
y –y = 2x2 + 4x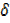 x + 2
x + 2 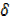 x2 +5 – [2x2 +5]
x2 +5 – [2x2 +5]
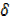 y = 4x
y = 4x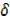 x+ 2
x+ 2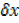 2……….(ii)
2……….(ii)
Dividing ii…………. By 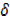 x
x
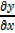 = 4x +2
= 4x +2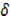 x………….iii…
x………….iii…
As 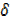 x
x 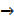 0,
0, 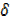 y
y 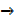 0
0
And
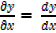
(iii) Becomes
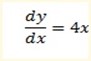
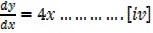
Note: The expression 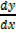 is called derivative of y with respect [w.r.t] to x
is called derivative of y with respect [w.r.t] to x
The process of finding derivatives is called DIFFERENTIATION.
Example
Differentiate y = x3 +1 with respect to x
Solution
Y +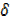 y = [x +
y = [x +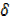 x]3 +1
x]3 +1
= x3+ 3x2
 x + 3x
x + 3x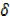 x2+
x2+ x3+1
x3+1
Subtracting y
y + 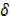 y-y = x3+3x2
y-y = x3+3x2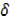 x+3x
x+3x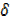 x2+
x2+ x3+1 – x3 – 1
x3+1 – x3 – 1
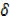 y = 3x2
y = 3x2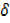 x+3x
x+3x 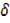 x2+
x2+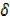 x3
x3
Dividing by 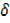 x
x
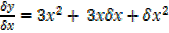
As 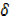 x
x 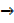 0,
0, 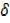 y
y 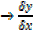
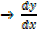

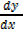 = 3x2
= 3x2
Examples
Find the gradients of the following curves
1.) 2x2-1
2.) y =x3-1
Solution
1) 2x2-1
y+ y = 2[x +
y = 2[x + x]2-1
x]2-1
y+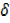 y =2 [x2+2x
y =2 [x2+2x 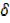 x+
x+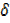 x2]-1
x2]-1
y+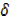 y = 2x2 +4x
y = 2x2 +4x  x+
x+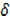 x2-1…………(i)
x2-1…………(i)
Subtracting y from(i)
y +  y – y = 2x2 + 4x
y – y = 2x2 + 4x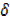 x +
x +  x2 – 1 – [ 2x2-1]
x2 – 1 – [ 2x2-1]
 y = 2x2+ 4x
y = 2x2+ 4x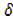 x+2
x+2 x2-1-2x2+1 ………………..(ii)
x2-1-2x2+1 ………………..(ii)
Dividing …..(ii) by  x
x
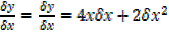
=4x + 2 ………(iii)
………(iii)
As 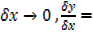
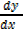
(iii) Becomes
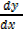 = 4x
= 4x
1. y = x3 – 1
Solution
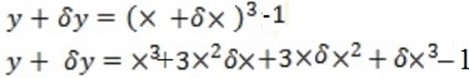
Subtracting y
y + 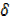 y-y = x3 + 3x 2
y-y = x3 + 3x 2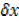 + 3x
+ 3x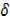 x2 +
x2 +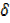 x3-1-x3 +1
x3-1-x3 +1
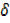 y =3x2
y =3x2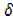 x+ 3x
x+ 3x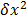 +
+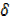 x3
x3
Dividing by 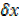
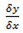 =
= 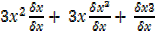
= 3x2 + 3x +
+ 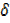 x2
x2
As 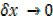 ,
, 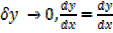
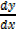 = 3x2
= 3x2
EXERCISE
Find the gradients of the following curves.
1.) y = x2
Solution
y + 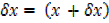 2
2
= x2 + 2x 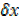 +
+  x2
x2
Subtracting y
y +  y-y= x2 + 2x
y-y= x2 + 2x  +
+ 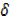 x2 -x2
x2 -x2
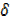 y = 2x
y = 2x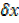 +
+ 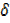 x2
x2
Dividing by 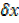
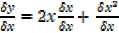
= 2x + 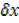
As 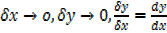
 = 2x
= 2x
2.) y= x3
Solution
y + 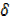 x = (x +
x = (x + 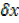 )3
)3
= x3 + 3x2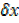 + 3x
+ 3x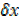 2 +
2 + 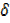 x3…….(i)
x3…….(i)
Subtracting y
y + 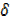 y-y=X3 + 3x2
y-y=X3 + 3x2 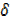 x + 3x
x + 3x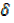 x2 +
x2 +  x3 – x3
x3 – x3
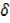 y= 3x2
y= 3x2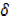 x + 3x
x + 3x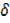 x2 +
x2 +  x3………….(ii)
x3………….(ii)
Dividing by 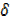 x
x
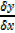 =
= 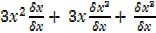
= 3x2 + 3x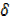 x +
x + 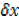 2
2
As 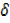 x
x 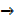 0 ,
0 , 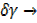 0 ,
0 , 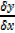 =
= 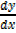
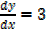 x2
x2
3.) y = x
solution
y + 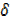 x = x +
x = x + 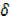 x………….(i)
x………….(i)
subtracting y
y +  y-y= x +
y-y= x + 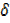 x – x
x – x
 y=
y= 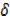 x ………..(ii)
x ………..(ii)
Dividing by 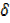 x
x
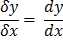
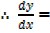 1
1
4.) y =3x2
Solution
y + 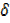 x = 3 [x +
x = 3 [x +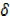 x] 2
x] 2
=3 [x2+ 2x  x +
x +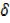 x2]
x2]
=3x2+6x 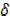 x+3
x+3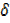 x2 -3x2……….(i)
x2 -3x2……….(i)
Subtracting y
y + 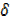 y-y= 3x2+6x
y-y= 3x2+6x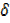 x+3
x+3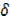 x2-3x2
x2-3x2
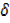 y= 6x
y= 6x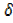 x+3
x+3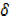 x2…….(ii)
x2…….(ii)
Dividing by 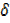 x
x
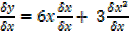
= 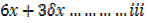
As 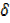 x
x  0,
0,  y
y 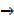 0,
0, 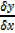 =
= 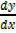
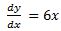
5.) y = x2 +3x
Solution
y + x = [x+
x = [x+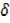 x]2 + 3[x+
x]2 + 3[x+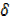 x]
x]
x2+2x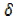 x+
x+ 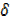 x2+ 3x+3
x2+ 3x+3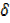 x…………i
x…………i
Subtracting y
y + 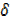 y-y = X2 + 2x
y-y = X2 + 2x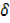 x+
x+ 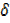 x2+3x +3
x2+3x +3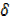 x -(x 2 + 3x)
x -(x 2 + 3x)
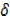 y = 2x
y = 2x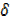 x +
x + 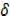 x2 + 3
x2 + 3 x……..ii
x……..ii
Dividing by 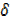 x
x
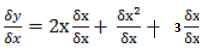
= 2x +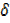 x +3
x +3
As 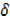 x →0,
x →0,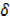 y → 0,
y → 0, 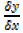 →
→ 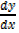
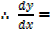 2x +3
2x +3