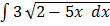SUB-TOPIC
1. The anti derivative
2. Indefinite integrals
3. Define Integrals
4 Application of integration
THE ANTI-DERIVATIVE
. Is the reverse of differentiation.
-In differentiation we start with function to find the derivative
-For anti derivative we start with derivative to find the function
Consider the table below
| FUNCTION | DERIVATIVE | ANTI-DERIVATIVE (INTEGRATION) |
| y=x2 | y1=2x |  =x2+c =x2+c |
| y=x3 | y1=3x2 | 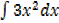 =x3 +c =x3 +c |
| y=4 | y1=0 | 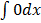 =c =c |
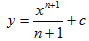 |
y1=xn |  = =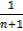 xn+1+c xn+1+c |
edu.uptymez.com
Integral notation
If y is the function of x, then 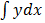 is known as integration of y with respect to x
is known as integration of y with respect to x
The integral sign cannot divorced with dx if we are integrating with respect to x.
Generally
If xn is integrated with respect to xn then
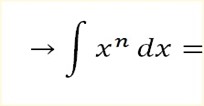 =
=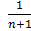 xn+1 + c
xn+1 + c
Examples
Find
a) 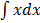
Solution
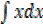 =
=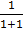 x1+1 + c
x1+1 + c
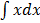 =
=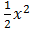 +c
+c
b) 
Solution
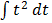 =
=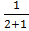 x2+1 + c
x2+1 + c
=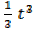 + c
+ c
c) 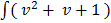 dv
dv
Solution
dv = 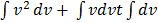
=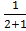 v2+1 +
v2+1 + 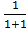 v1+1 + v + c
v1+1 + v + c
= 
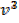 +
+ 
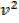 + v + c
+ v + c
EXERCISE
Integrate the following
1. 
2. 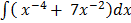
3. 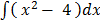
4. 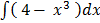
Solution
1. 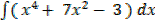
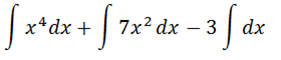
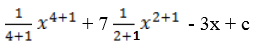
= 
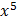 + 7
+ 7 
 – 3x + c
– 3x + c
= 
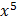 + 7
+ 7 
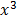 – 3x + c
– 3x + c
2.  dx
dx
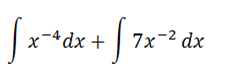
= 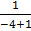
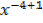 +
+ 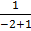 7
7 + c
+ c
= 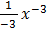 +
+ 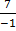
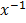 + c
+ c
= 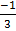
 -7
-7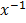 + c
+ c
2. INDEFINITE INTEGRALS
Is an integral which does not have limits at the ends of the integral sign.
An arbitrary constant must be shown
e.g. 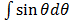 ,
,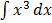 ,
, 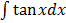 e.t.c
e.t.c
Example
Integrate the following with respect to X
1. 5 -7x+8
-7x+8
2. 2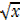 –
– 
3. 4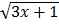
Solution
1. 1.
= 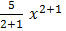 –
– 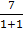
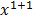 + 8x + c
+ 8x + c
= 
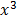 –
– 
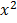 + 8x + c
+ 8x + c
2. 2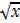 –
–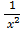
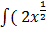 –
– 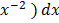
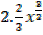 +
+ 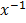 + c
+ c

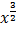 +
+  + c
+ c
Or
 (
( 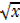 )3 +
)3 +  + c
+ c
3. 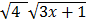 dx
dx
Let u=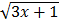
u2=3x+1
2udu=3dx
dx = 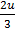 du
du
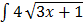 dx =
dx = 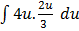
= 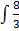
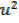 du
du
= 
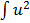 du
du
=  x
x 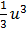 + c
+ c
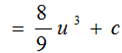
But u =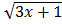
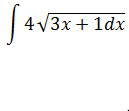
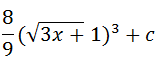
EXERCISE
Integrate the following
1. 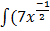 – 5
– 5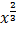 + 12) dx
+ 12) dx
2. 
3. 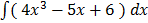
4.