ADVANCED MATHEMATICS FORM 5 – ALGEBRA

Indices (law of exponents)

Three basic rules including the Indices are:

            i) a^m x aⁿ = a^{m + n}

            ii) a^m ÷ aⁿ = a^{m – n}

            iii) (a^m) ⁿ = a^m

Negative indices

Consider a⁵ ÷ a² = a^{5
– 2} = a³                                                                                                                        

                        = a² ÷ a⁵ = a^{2
– 5} = a ^-3 

In general

                        a ^-m =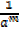

Fractional indices

Consider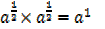

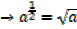
Similarly

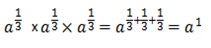
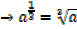
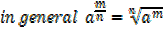
Zero exponents

Consider a^m x a^o = a^{m + o}

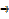                        a^o = 1

Laws of logarithm

If a and b are two positive numbers there exist a third number c such that 

a^c = b

            →c is the logarithm of b to base a

            i. e 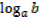 = c

           

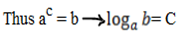
Definition

Logarithm of ‘x’ to base ‘a’ is the power to which ‘a’ must be raised to give ‘x’.

If p = 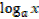 and q =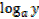, then 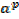= x and  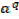= y

Thus

1.     

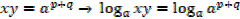
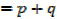
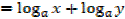
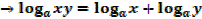
2.     

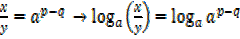
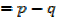
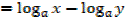
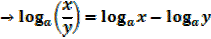
3.     

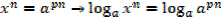
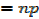
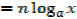
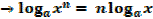
Change of base

If y =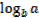

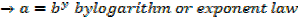
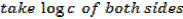
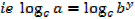
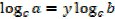
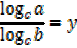
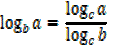
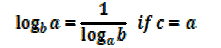
EXAMPLE

1.                  Solve for x,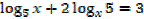

Solution

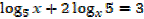
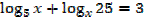
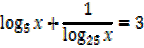
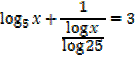
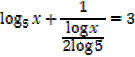
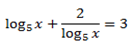
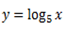
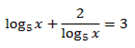
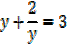
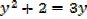
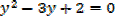
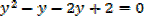
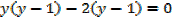
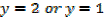
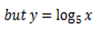
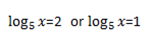
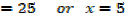
Note that:

There are two important bases of logarithms

10 and e

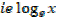
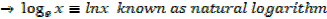
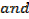
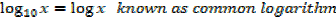
Series

A series is the sum of a sequentially ordered finite or infinite set of terms

Finite series

–      Is the one have defined first and last term e.g. 1 + 3 + 5 + 7 + 9 + 11…… + 21 is a finite series

Infinite series

–      Is the one have defined the first but not the last term e.g. 1 + 3+ 5+ 7+ 9+ 11+ …..

In both cases the first term is 1

The sigma notation

∑ stands for ” sum of ”

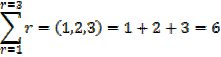
e.g.

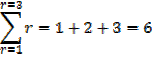
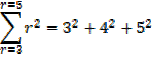
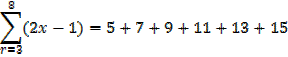
Exercise

Discuss the following  and find the sum if n = 8

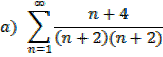
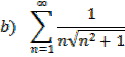
The sum of the first n natural numbers

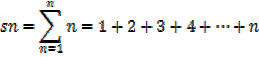
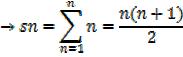
The sum of squares of the first n natural numbers

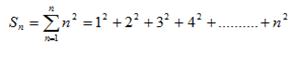
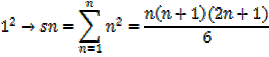
The sum of the cubes of the first n natural numbers

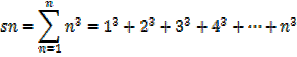
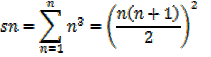
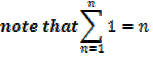
Example

                                I.    If a_n = n² + 3n + 1 determine an expression for n        

             

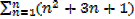
                             II.     If a_n = n³ + 2n² + 4n evaluate

a) a₁    b) a₄    c)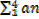                                                                   

The sum of the first n natural numbers

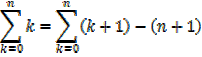
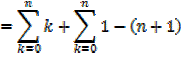
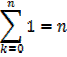
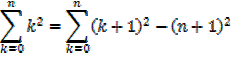
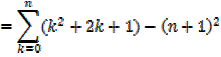
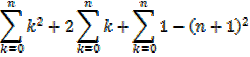
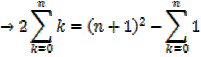
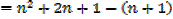
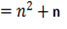
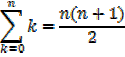
The sum of the squares of the first n natural numbers

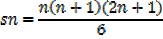
Proof,

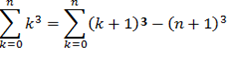
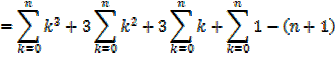
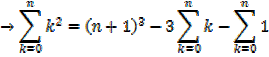
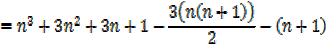
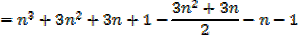
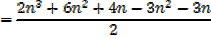
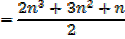
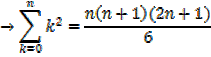
Exercise

1.       Evaluate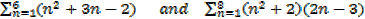      

Proof by the mathematical induction

Example

            Prove that n (n² + 5) is exactly divisible by 3 for all positive integers n

Proof: I

            Let n = 1;          1(1² + 5) = 6 = 3 x 2

                        n = 2;       2 (2² + 5) = 18 = 3 x 6

                        n = 3;      3 (3² + 5) = 42 = 3 x 14

                        n = 4;       4 (4² + 5) = 84 = 3 x 28

                        n = 7;        7 (7² + 5) = 378 = 3 x 126

Proof: II

                i) Let n = 1 = 1 (1² + 5) = 6 = 3 x 2

               ii) Let n (n² + 5) be divisible for n = k

                        i.e. k (k² + 5) = 3p, where p is any integers

               iii) When n = k + 1

                        (k + 1) ( (k +1)² + 5) = (k + 1) (k² + 2k + 1 + 5)

                                                           = (k + 1) ((k² + 5) + (2k + 1))

                                                           = k (k² + 5) + k (2k + 1) + (k² + 5) + (2k +1)

                                                           = 3p + 2k² + k + k² + 5 + 2k +1

                                                           = 3p + 3k² + 3k + 6

                                                           = 3 (p + k² + k + 2)

Since p and k are positive integers

So the number in the bracket is positive

            iv) Since when n = 1 the values 1 (1² + 5) is divisible by 3 then the value n (n² + 5) will be divisible by 3 for n = 2, n = 3, n = 4…… by the above  working

            →n (n² + 5) is divisible by 3 for all    n∈
⁺

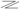Principle of proof by mathematical induction

It states if s₁, s₂, s₃…..Sn…. is a sequence of statements and if

                                                    i) s₁ is true

                                                    ii) Sn → Sn _{+ 1}, n = 1, 2, 3 … are true, then s₁, s₂, s₃…… Sn… are true statement

Examples

1.  Prove by mathematical induction that 2 + 4+ 6 +…..2n = n (n + 1)

            Solution

            When n = 1

                        L. H. S = 2, R. H. S = 1(1 + 1) = 2

                        L. H.S = R. H. S

            It is true for n = 1

Let the statement be true for n = k

            2 + 4 + 6 + …. 2k = k (k + 1)

Required to prove when n = k + 1

2 + 4 + 6 + …… 2k + 2(k + 1) = k (k + 1) + 2(k + 1)

                                                           = k² + k + 2k + 2

                                                           = k² + 3k + 2

                                                           = k² + k + 2k + 2

                                                           = k (k + 1) + 2 (k + 1)

                                                           = (k + 1) (k + 2)

Which is the same as putting n = k + 1 in the formula

Since n = 1gave a true statement, n =2, n = 3, n = 4… will be true statement as worked above

2.   2. Prove by induction that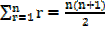

            Solution

            Proof:            

            When n = 1,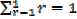

            Also n = 1 give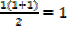

                                   L.H.S = R. H. S

            Let the statement be true for n =k

            Let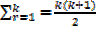     

Required to prove when n = k + 1

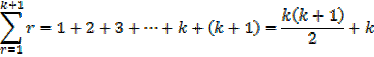
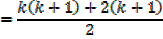
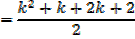
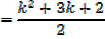
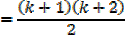
            Which is the same as putting n = k + 1 in the form

            Since n = 1 gave a true statement

            n = 2, n = 3, n = 4… will give true statement

3. Prove that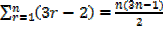 

            Solution

            Proof:

                        When n = 1

                        L.H. S = 3 x 1 – 2 = 1

                        R.H.S =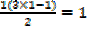                                                                                             

                        L.H.S = R.H.S

            Let the statement be true for n = k                      

            I.e. 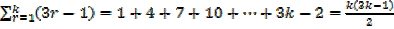        required to prove when n = k + 1

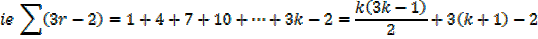
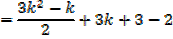
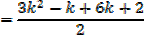
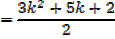
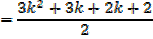
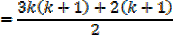
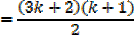
            Which is the same as putting n = k + 1 in the formula since n = 1 gave a    true statement,

            n =2, n = 3, n = 4 … will give true statement