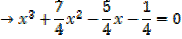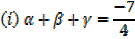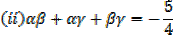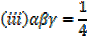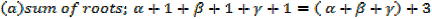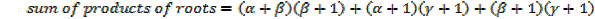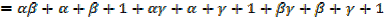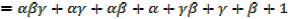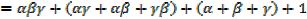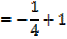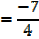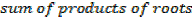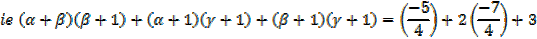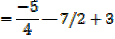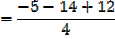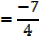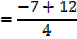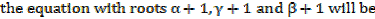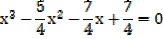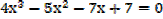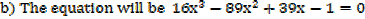Roots of a polynomial function
If  and
and  are roots of quadratic equation
are roots of quadratic equation
Then (x –  ) (x – β) = 0
) (x – β) = 0
x2 – βx – 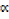 x +
x + 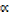 β = 0
β = 0
x2 – (β +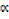 ) x +
) x + 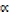 β = 0
β = 0
Given a quadratic equation as
ax2 + bx + c = 0, where a, b, c, are constant
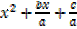
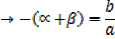
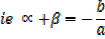
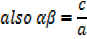
Summary
A quadratic equation is given by
x2 – (sum of factors) x + products of factors = 0
Example
1. Given 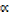 and β as the roots for 4x2 + 8x + 1 = 0 form an equation whose roots are
and β as the roots for 4x2 + 8x + 1 = 0 form an equation whose roots are 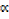 2 β and β2
2 β and β2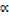
Solution
Sum of roots 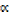 2 β + β2
2 β + β2  =
= 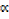 β (
β (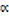 + β)
+ β)
Products of root are (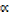 2 β) (β2
2 β) (β2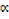 )
)
=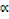 3 β3
3 β3
= ( β) 3
β) 3
(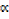 2 β) (β2
2 β) (β2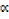 ) = (
) = (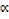 β) 3
β) 3
The given equation can be written as
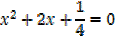
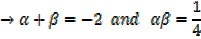
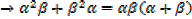

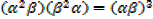
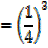
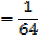
The required equation is
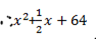 =0
=0
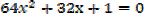
2. The equation 3x2 – 5 + 1 = 0 has roots 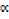 and β
and β
a) Find values of 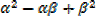
b) Find the values of 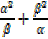
Solution
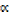 + β =
+ β =  and
and 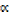 β =
β = 
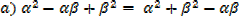
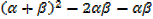
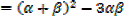
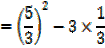
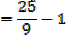
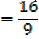


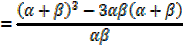
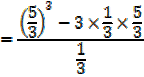
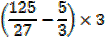
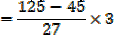
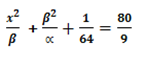
Roots of cubic equations
If , β,
, β, 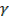 are roots of a cubic equation then
are roots of a cubic equation then
(x –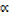 )(x – β)(x – γ) = 0
)(x – β)(x – γ) = 0
(x2 – 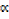 x – βx +
x – βx + 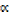 β) (x – γ) = 0
β) (x – γ) = 0
x3 – γx2 –  x2 +
x2 +  γx – βx2 + βγx +
γx – βx2 + βγx + 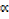 βx –
βx – 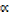 βγ = 0
βγ = 0
x3 – ( + β + γ) x2 + (
+ β + γ) x2 + (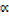 γ+ βγ +
γ+ βγ + 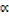 β) x –
β) x – 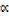 βγ = 0
βγ = 0
x3 – (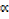 + β + γ) x2 + (
+ β + γ) x2 + (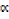 γ + βγ +
γ + βγ + 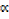 β) x –
β) x –  βγ = 0
βγ = 0
Given cubic equation can be written as
ax3 + bx2 + cx + d = 0
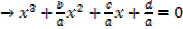
Equating coefficients of x2, x and the constant terms
i) 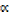 + β + γ =
+ β + γ = 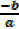 -; sum of roots
-; sum of roots
ii) 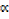 γ + βγ +
γ + βγ + 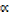 β =
β =  ; sum of products of roots
; sum of products of roots
iii) 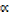 γβ =
γβ = 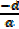 ; products of roots
; products of roots
Examples
1. The equation 3x3 + 6x2 – 4x + 7 = 0 has roots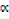 , β, γ. Find the equations with roots
, β, γ. Find the equations with roots
a)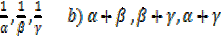
Solution
From
x3 – (sum of factors) + (sum of products of factors) – products = 0
X3 – (sum of factors) x2 + (sum of products of products of factors) x – products = 0
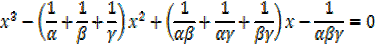
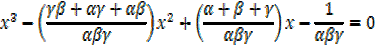
From the equation 3x3 + 6x2 – 4x + 7 = 0
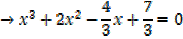
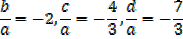
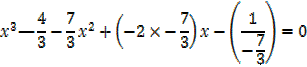


2. If the roots of the equation 4x3 + 7x2 – 5x – 1 = 0 are  , β and γ find the equation whose roots are
, β and γ find the equation whose roots are
a)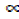 + 1, β + 1, γ + 1 b)
+ 1, β + 1, γ + 1 b) 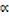 2, β2, γ2
2, β2, γ2
Solution
4x3 + 7x2 – 5x – 1 = 0