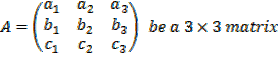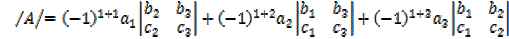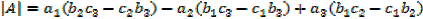Remainder and factor theorem
Definition:
A polynomial is an expression of the form
anxn + an – 1 x n – 1 + an – 2 x n -2 + …… + a1x + a0
Where an, an – 1, an – 2 …a1, ao are real numbers known as coefficients of the polynomial
→an
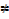 0
0
→anxn is the leading term
→n is called the degree of the polynomial
Normally the polynomial is written as p (x) = anxn + an – 1xn– 1+ … + a1x + ao
P (x) = anxn + an – 1xn -1 + …. + a1x + ao
e.g.
p (x) = 2x4 – 3x3 + 10x3 + 10x2 – x + 11
p (x) = x5
p (x) = 2x2 – 3x + 10
p (x) = 6x3 – 22x2 – 12
p(x) = 3x – 2
p (x) = 17
To divide a polynomial p (x) by another polynomial D (x) means finding polynomial Q (x) and r (x)
Such that
P (x) = D (x) Q (x) + r (x)

Where p (x) is called a dividend
Q (x) is called a quotient
D (x) is called divisor
r (x) is called remainder
Note that the degree of r (x) < D(x)
The remainder theorem
When a polynomial p (x) is divided by a linear factor (x – a) the remainder is P (a)
When a linear factor is in the form kx – b then it should be put in the form k(x – 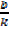 ) and the remainder is then P (
) and the remainder is then P (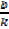 )
)
Proof:
Let P (x) = (x – a) Q(x) + R
Where Q (x) is a polynomial and R is the remainder when x = a
→P (a) = (a – a) Q (a) + R
P (a) = R
R = P (a)
When R = 0
P (x) = (x – a) Q(x)
x – a is a factor or p (x)
Since p (a) = 0
”a” is a root (a zero) of p(x)
Examples
1. Find the remainder when x5 + 4x4 – 6x2 + 3x + 2 is divided by x + 2
Solution
P (x) = x5 + 4x4 – 6x2 + 3x + 2
x – a = x + 2
a = -2
p(-2) = (-2) 5 + 4(-2)4 – 6 (-2) 2 + 3x – 2 + 2
p(-2) = -32 + 64 – 24 – 6 + 2
= 66 – 62
= 4
P(-2) = 4
2. Find the remainder when 4x3 – 6x2 – 5 is divided by 2x – 1
Solution
P (x) = 4x3 – 6x2 – 5
x – a = (x – ½)
P  = 4
= 4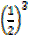 – 6 x
– 6 x 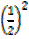 – 5
– 5
= 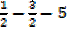
= 1 – 3 – 10
2
P (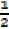 ) = -6
) = -6
Factors theorem
If ‘a’ is a zero of p (x) then (x – a) is a factor of p(x) i.e. p(x) = (x – a) Q (x)
Proof:
Let p (x) = (x – a) Q(x) + R
Given ‘a’ is a zero of p (x)
Then p(a) = 0
0 = (a – a) Q (a) + r
0 = r
r = 0
p (x) = (x – a) Q(x)
x – a is a factor of p (x)
Examples
Factorize completely the following polynomial function x4 – 5x3 + 6x2 + 2x – 4
Solution
Let p(x) = x4 – 5x3 + 6x2 + 2x – 4
P (1) = 1 – 5 + 6 + 2 – 4
= 0
P (2) = 24 – 5 (2)3 + 6 (2) 2 + 2 x 2 – 4
= 16 – 40 + 24 + 4 – 4
= 0
(x – 1) and (x – 2) are factors of P (x)
→P (x) = (x – 1)(x – 2) Q(x)
P (x) = (x2 – 3x + 2) Q(x)
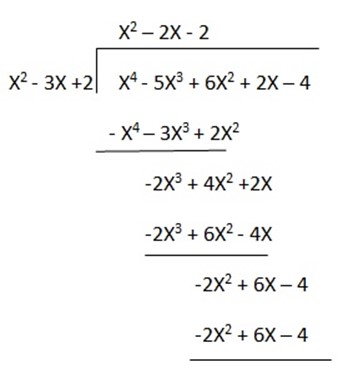
Q (x) = x2 – 2x – 2
= (x2 – 2x + 1) – 3
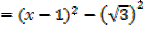
= ((x – 1) +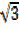 ) ((x – 1) –
) ((x – 1) –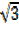 )
)
→P (x) = (x – 1) (x – 2) (x – 1) +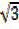 ) (x – 1) –
) (x – 1) –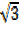 )
)
Synthetic division
Synthetic division is the shortcut method to find the remainder when a polynomial function is divided by a factor x – a
Example
1. Use synthetic division to divide 2x3 + x2 – 3x + 4 by x + 3
Solution
x – a = x + 3
So; a = -3
Then
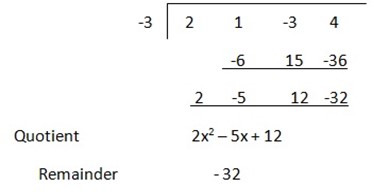
Note that in the synthetic division the third row will contain the coefficients of the quotient and the remainder
2. Use synthetic division to divide 4x3 – 6x2 – 5 by 2x -1
Solution
x – a = 2x – 1
a = ½

Q (x) = 4x2 – 4x – 2
Remainder = -6
Rational zero theorem
Let p (x) = anxn + an – 1xn – 1 + ….. + ax + ao
Where
an, an – 1, a1, a0 are integral coefficients and
Let 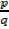 be a rational number in its lowest term
be a rational number in its lowest term
Then if is 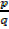 a zero of p (x) when p is a factor of a0
a zero of p (x) when p is a factor of a0
q Is a factor of an
Example
To find zero of 2x3 – x- 3
If 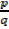 is a zero of the expression
is a zero of the expression
Then p is a factor of -3 ie -1, 1, -3, 3
2 i.e. 1, -1, 2, -2
We try -1, 1, -3, 3, 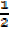 , ½, -3/2, and 3/2
, ½, -3/2, and 3/2
Partial fraction (decomposition of fraction)
The process of decomposition of fraction depends on one of the following;
1)To every linear factor ax + b in the denominator there corresponds a fraction of the form
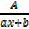
2) To every repeated factor like (ax + b)n in the denominator there corresponds n fractions of the form 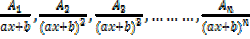
3) To every factor of the form anxn + an – 1xn – 1+….. + a1x + a0 in the denominator there correspond fraction of the form 
4) If the degree of the numerator is greater than or equal to the degree of denominator, division is ennglish-swahili/courage” target=”_blank”>couraged and the remainder is treated as in (1), (2) 0r (3)
Examples
1. Express in partial fraction

Solution
Let 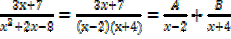
Where A and B are constant
3x + 7 = A (x + 4) + B (x – 2)
3x + 7 = Ax + 4A + Bx – 2B
3x + 7 = (A + B) x + 4A – 2B
3→x = (A + B) x
3 = A + B…. (i)
7 = 4A – 2B…. (ii)
2 (i) + (ii) gives
13 = 6A → A = 
From (i)
3 = 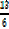 + B
+ B
18 = 13 + 6B
5 = 6B
B = 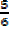
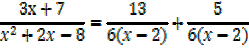
2. 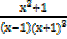
Solution
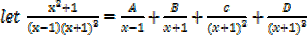
x2 + 1 ≡ A (x + 1)3 + B (x + 1)2 (x – 1) + C (x + 1) (x – 1) + D (x – 1)
When x = 1
2 = 8A →A =
When x = -1
2 = -2D → D = -1
When x = 0
1 = A – B – C – D
1 = ¼- B – C – (-1)
4 = 1 – 4B – 4C + 4
1 = 4B + 4C …… (i)
When x = -2
5 = -A – 3B + 3C – 3D
5 = –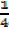 – 3B + 3C + 3
– 3B + 3C + 3
20 = -1 – 12B + 12C + 12
9 = -12B + 12C

4 = 8C
C = ½
From (ii)
3 = -4B + 4 x ½
3 = -4B + 2
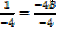
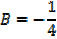
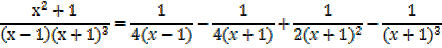
QUESTION
4. Express x4 + x3 – x2 + 1 into partial fraction
(x – 1) (x2 + 1)
Quadratic inequalities
A quadratic inequalities is an inequality of one of the following four types
ax2 + bx + C < 0
ax2 + bx + C ≤ 0
ax2 + bx + C > 0
ax2 + bx + C ≥ 0
Where a, b and c are real numbers and a  0
0
Solving quadratic inequality
Solving quadratic inequality involves changing inequality signs to equal sign to obtain the associated quadratic equation.
E.g. x2 + x – 2 ≤ 0 – quadratic inequality
x2 + x – 2 = 0 – associated quadratic equation
Example
1. Solving the following inequality
x2 + x – 2 ≤ 0
Solution
x2 + x – 2 = 0
x2 – x + 2x – 2 = 0
x (x – 1) + 2 (x – 1) = 0
X = -2 and x = 1
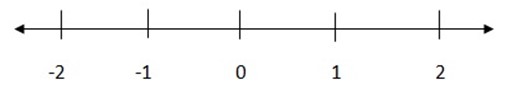
Testing the values
Test value -3
4≤ 0 False
Test value – 0
-2 ≤ 0 True
Test value 2
4 ≤ 0 False
→-2 ≤ x ≤ 1
2. Solve the following quadratic inequality
X2 – 3 > 2x
Solution
X2 – 3 > 2x = x2 – 2x – 3 > 0
Then,
x2 – 2x – 3 = 0
x2 + x- 3x – 3 = 0
x (x + 1) – 3(x + 1) = 0
(x + 1) (x – 3) = 0
x = -1 and x = 3
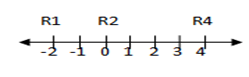
Test value -2
1 > – 4 → true
Test value 0
-3 > 0 → false
Test value 4
13 > 8 = true
x < -1 and x > 3
Exercise
Solve the following inequalities
a) (x – 2) (x – 1) > 0
b) (3 – 2x) (x + 5) ≤ 0
c) (1 – x) (4 – x) > x + 11
d)  x2 – 2x + 3 > 0
x2 – 2x + 3 > 0
e) 3x + 4 < x2 – 6 < 9 – 2x
Rational inequalities
Examples
1. Solve the inequality
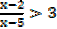
Solution
1st Make one side equal to 0
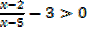
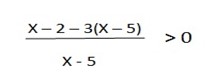
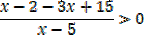

Do not multiply by denominator since x – 5 is not known as positive or negative
2nd find real numbers that make either the numerator or the denominator equal to 0
I.e. -2x + 13 = 0
2x = 13
X = 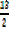 makes numerator = 0
makes numerator = 0
And x – 5 = 0
X = 5 makes the denominator = 0

Test value 4
-5 > 3 → false
Test value 6
4 > 3 → true
Test value 7
 > 3 – false
> 3 – false
= 5 < x < 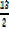
2. Solve the inequality
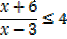
Solution
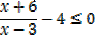
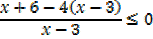
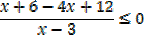
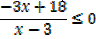
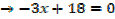
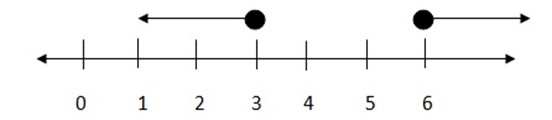
X = 6 makes the numerator = 0
X = 3 makes the denominator = 0
3. Find the possible values of x for which 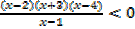
Solution
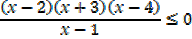
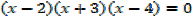
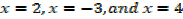
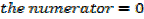

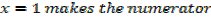

Test value P
-24 ≤ 0 →True
Test value -4
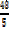 < 0 false
< 0 false
Test value 2
0 < 0→ true
Test value 5
4 < 0 → false
→2< x < 4
Exercise
What values of x satisfy in each of the inequalities?
A. 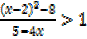
B. 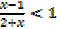
C. 
D. 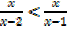
Absolute value inequality
Examples
Solve the following inequalities
a) |2x – 3| < 5
b) |x – 2| > -3
c) |2x + 3| < 6
Solution
a) |2x – 3| < 5
2x – 3 < 5 or 2x – 3 > -5
2x < 8 2x > -2
x < 4 or x > -1

Examples
Solve the following inequalities
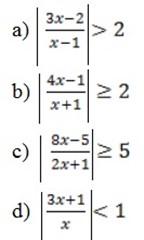
Solution
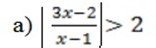
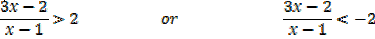
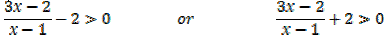
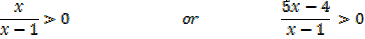
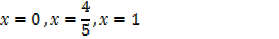

X < 0, 0.8 < x < 1 and x > 1
Determinant of a 3 x 3 matrix
Let