Algebra is a study which deals with situations whereby some values unknown. Normally these unknown are represented by letters. Those letters are also referred to as variables.
Algebraic expression
An expression – is a mathematical statement which consists of several variables. An expression can only be simplified, that is we cannot find values of the variables (s) on it.
Examples
1. a + 2
2. x + 3y + 9z
3.16p – qp
4. a + b + c + d
5. 40
An equation
An equation is formed when two expression are joined by an equal sign
E.g
i) 2x – y = 16
ii) x + 2 = 6 – 5
iii) 3y + xy = 9
Each member of an equation or expression is called Term
Coefficient
When a number is multiplied by a variable (s) that number is called coefficient of that variable
Example
What is the coefficient of the variables in the following?
a) 6x – 8p + y
b)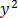 
– k + 3d
c) 2a + 3b – c
Solutions
Coefficients of a) x is 6
y is 1
P = -8
b) K = -1
d = 3,
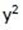= 1
c) a = 2
b = 3
c = -1
Addition and subtraction of algebraic expression
Addition and subtraction of algebraic expression can be done by adding or subtracting like term.
Like terms are those terms which has identical (same) variables
Examples
1. 2a + 4a = 6a
2. 5a + 16a = 21a
3. 2x + 10x – 3x = 9x
Examples: simplify the expression
3n – 7n + 12n
Solution
-4n + 12n
12n – 4n
∴= 8n
Examples: simplify
6m – 4 – 2m + 15
Soln
6m – 2m – 4n + 15
= 4m + 11
Example: simplify 4x + 6y – 3x + 5y
Solution
4x – 3x + 6y + 5y
= x + 11y
Coefficient: y = 11
x = 1
Number of terms = two
Exercise 7.1
1. Simplify each of the following expressions and after simplifying state
a. the number of terms
b. the coefficient of each of the terms
i) n + n + n + n + n + k + k + k + x + x = 5n + 3k + 2x
Solution
(a) There are3 terms
(b) Coefficient of “n” is 5
Coefficients of “y” is 3
Coefficients of “x” is 2
ii) 3x + 4y – 7z + 3x – 7y + 2z
Solution
a) There are 3 terms
6x – 3y – 5z
b) coefficients of x is 6
Coefficients of y is -3
Coefficients of z is -5
iii) 3
x + 7x – 
x =
Solution
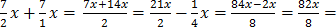
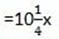
a) There is 1 term
b) Coefficient of x is 10
Simplify each of the expressions in numbers 2 – 6
2. 12m + 13m
12m
+ 13m
25m = 25m
3. 5y + 7y – 4y
12y – 4y
= 8y
4. 24w – 28w
-28w + 24w
= -4w
5. 15n – 9n
15n – 9n
= 6n
6. 4k – k + 3k
3k + 3k
= 6k
7. 8y – 3 – 7y + 4
8y – 7y – 3 + 4
y + 4 – 3
y + 1
= y+ 1
8. 14x + 8 – 3x + 2
14x – 3x + 8 + 2
=11x + 10
9. 3a – 5b – 7a + 6c + 7a + 8b
3a – 7a + 7a – 5b + 8b + 6c
=3a + 3b + 6c
10. 4x – 6y + 7x + 2y
4x + 7x – 6y + 2y
=11x – 4y
11. 3x + 4 + 8x – 4 – 11x
3x + 8x – 11x + 4 – 4
11x – 11x + 4 – 4
0 + 0
= 0
12. 8m + 0.4m – 2 – 6m + 8
8m + 0.4m – 6m – 2 + 8
8.4m – 6m + 6
= 2.4m + 6
Multiplication and division of algebraic expression
Example:1) Multiply a – 2b + 6ab by 12xy
Solution
(a – 2b + 6ab) x 12xy
= 12axy – 24bxy + 72abxy
Examples:2) Re – write without brackets
– 16a (-2mn + 9xb – 3kbc)
Solution
-16a (-2mn+9xb-3kbc) = (-16ax-2mn) + (-16a x 9xb) + (-16a x -3kbc)
= 32amn + -144axb + 48abck
= 32amn – 144axb +48abc
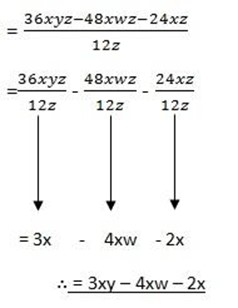
Example:3) divide 36xyz – 48xwz – 24xz by 12z
Solution
(36xyz – 48xwz – 24xz) ÷ 12z
Exercise 7.2
1. Complete the following
60xy – 30y + 90z = 30 ( )
Solution
60xy – 30y + 90z = 30 (2xy – y +3x)
2. Simplify i) xy + yz + 2xy – 3zy
ii) 8m ÷ 2 + 3mn ÷ n
Solution
i) xy + yz + 2xy – zy ⇒ xy+yz +2xy – zy = xy + 2xy +yz – 3zy
= 3xy – 2yz
ii) 8m ÷ 2 + 3mn ÷ n
4m + 3m
(4 + 3) m
=7m
3. Simplify the following
i) 5mn – 3mn
= 2mn
ii) xyz + 3xy + 4zx – zyx
= xyz – zyx + 3xy + 4zx
= 0 + 3xy + 4zx
= 3xy + 4zx
iii) 3 (2n + 3) + 4 (5n – 3)
Solution
6n + 9 + 20n – 12
6n + 20n + 9 – 12
=26n – 3
iv) abc + bac – cab
Solution
abc + abc – abc
abc – abc + abc
abc + 0
= abc
v) 2 (5x + 3y) + 3(3x + 2y)
Solution
10x + 6y + 9x + 6y
10x + 9x + 6y + 6y
= 19x + 12y
vi) m (2n + 3) + n (3m + 4)
Solution
2nm + 3m + 3mn + 4n
2nm + 3mn + 3m + 4n
= 5mn + 3m + 4n
vii) x (y – 5) + y (x + 2)
Solution
xy – 5x + yx + 2y
xy + yx – 5x + 2y
= 2xy – 5x + 2y
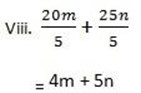
ix) Pq -2qp + 3pq – 2qp
Solution
Pq + 3pq – 2qp – 2qp
4pq – 4pq
= 0
x) (4x + 8y) ÷ 2 + (9xw + 4xy) ÷ w
solution
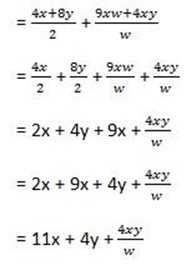
xi) Multiply 6a – 5b by 3x
Solution
3x (6a – 5b) = 3x x 6a – 3x x 5b
= 18ax – 15bx
∴= 18ax – 15bx
Equations
An equations is a mathematical statement which involves two expression connected or joined by an equal sign
So we define an equation also as statement of equality e.g. 2y – 6 = 3x + 12
The values of variables can be found in equation if the number of equations is equal to the number of unknown.
FORMULATION OF AN EQUATION
There are three steps to follow when formulating an equation which are;
i) Understand the problem/question, what it is asking for
ii) Let the unknown be represented by a variable
iii) Formulate the equation using the given information
Signs, words or phrase used when formulating an equation:-
+ Addition, sum of, increase by, greater than, plus, taller than, more than
– Difference, subtract, decrease, less than, shorter than.
× Multiplication, times, products.
÷ Division, divided, Quotient.
= Equals, is, given, result.
Example 01
1. The age of the father is equal to the sum of the ages of his son and daughter. If the son’s age is thrice the age his sister, formulate an equation.
Solution
Let y be the father age
And x be the age of the daughter
The age of son = 3x
y = 3x + x
y = 4x
2. The sum of two numbers is 20. If one of the number is 8 formulate an equation.
Solution
Let one of the number be x
And the other number = 8
x + 8 = 20
3. A girl is 14 years old, how old will she be in x years time
Solution
A girl = 14 years
Let “y” be a girls age in x years time.
In years time = + x
∴y = 14 + x
4. The difference between 24 and another number is 16, form an equation
Soln
Let another number = x
∴ 24 – x = 16
Exercise 7.3
Formulate equations for each of the following
1. Five times a number gives twenty
Soln
5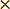 
x= 20
5x = 20
2. The difference between 123 and another number is 150
Solution
let another number = x
Then x – 123 = 150
∴ x – 123 = 150
3. The sum of 21 and another number is 125
solution
let another number = y
Sum means (+)
21 + y = 125
∴ 21 + y = 125
4. When a certain number is increased by 15, the result is 88
solution
Let the number be x
Then x + 15 = 88
x + 15 = 88
5. When 99 is increased by a certain number the result is 63
Solution
Let the number = y
Then 99 + y = 63
∴ 99 + y = 63
6. The product of 12 and another number is the same as two times the sum of 12 and the number
Solution
Let the number be x
Then 12 x x = 2 x (12 + x)
∴ 12x = 24 + 2x
7.A number is such that when it is double and 8 added to it, the result is the same as multiplying the number by 3 and subtracting 7.
solution
Let the number be x
Then x + x + 8 = x x 3 – 7
2x + 8 = 3x – 7
8. When 36 is added to a certain number, the result is the same as multiplying the number by 5.
solution
Let x be the number
Then x + 36 = x x 5
∴ x + 36 = 5x
9. If John is n years old and is 6 years older that James older, write an expression of the sum of their ages.
Solution
Let “J” be john, and “Q” be James and “N” be the year
Let Q = q years
J = n + 6 years
The sum of their age = q + n + 6
∴ = q + n + 6
10. When the sum of n and (n + 3) is multiplied by 5 the result half the product of the two numbers.
Write the expression of this statement:-
Solution
(n + (n +3) x 5 = ½ (n + (n +3) )
(2n + 3) x 5 = ½(2n + 3)
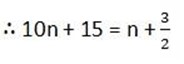
SOLVING FOR EQUATIONS
Solving means finding the value of the unknown in the equation
Example 1
1. x + 5 = 8
Solution
x + 5 = 8
x + 5 – 5 = 8 – 5
x + 0 = 3
x = 3
2. x – 8 = 15
x – 8 + 8 = 15 + 8
x = 23
3. 3x – 5 = 7
3x – 5 + 5 = 7 + 5
3x = 12
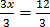
x = 4
4. 
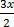+ 3 = 12
solution;
multiply 2 both side
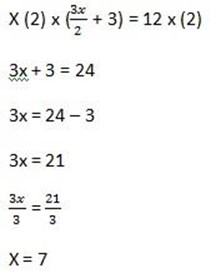
5. 
(3x – 2) = 10
Solution
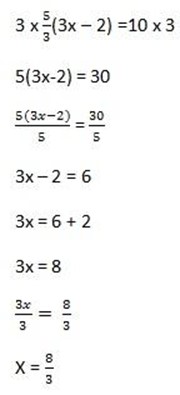
6. 
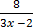= 2
Solution
= 
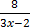8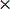 
1 = (3x – 2)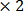
8 = 6x – 4
8 + 4 = 6x – 4 + 4
12 = 6x
= 
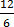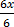
x = 2
7. 
– 
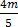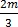= 4
Solution
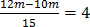
2m = 4 x 15
2m = 60
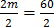
m= 30
8. 
+ 
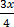= 5
Solution
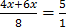
10x = 5 x 8
10x = 40
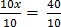
x = 4
9. 2x – 5 = 3x – 8
Solution
3x-8=2x-5
3x-2x=8-5
x = 3
10. 4 – 3t = 0.3t – 5.9
Solution
4 + 5.9 = 0.3t + 3t
9.9 = 3.3t
9.9 = 3.3t
3.3 3.3
t = 3
11. 
+ 
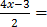
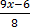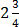
Solution
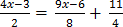
Multiply by 8 both side
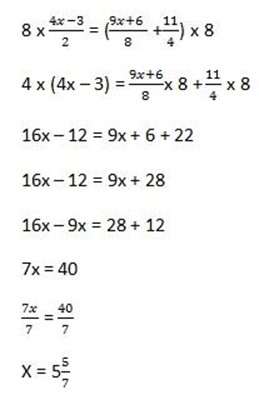
12. 
= 
– 
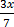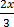solve for x
Solution
= 
– 
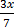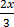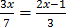
7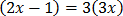
14x-7 = 9x
14x -9x =7
5x = 7
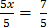
x = 
EXERCISE 7.4
Solve the following equations
1. x + 12 = 25
Solution
x = 25 – 12
x = 13
2. 
= 
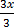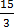
x = 5
3. 2x + 12 = 25
Solution
2x + 12 – 12 = 25 – 12
2x + 0 = 13
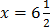
4. x – 8 = 8
Solution
x– 8 + 8 = 8 + 8
x = 16
5. x = 5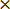
5
Solution
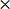X = 5
5
X = 25
6. 2x – 8 = 8
Solution
2x =8+8
2x = 16
= 
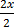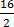
x = 8
7. 3x – 3 = 15
Solution
3x – 3 + 3 = 15 + 3
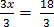
∴x =6
8. 
– 3 = 5
Solution
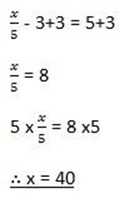
9. 0.2x + 7 = 9
Solution
0.2x + 7 – 7 = 9 – 7
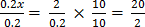
∴x = 10
10. 0.6x – 5 = 7
Solution
0.6x – 5 + 5 = 7 + 5
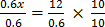
∴ x = 20
11. 
+ 3 = 5
Solution
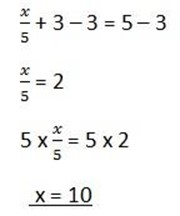
12. 4x – 7= 7
Solution
4x = 7 + 7
4x = 14
= 
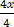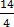
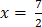
13. 
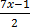= 14
Solution
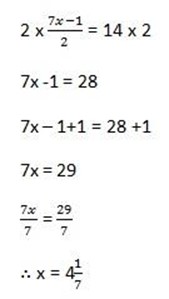
14. 
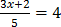
Solution
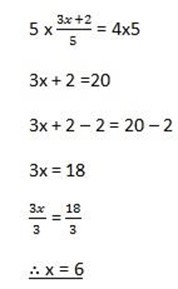
15. 
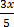= 6
Solution
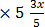= 6 x 5
=
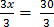∴x = 10
16. 
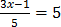
Solution
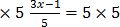
3x = 25 + 1
=
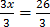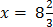
17. 
= 10
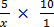
5 = 10x
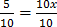
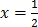
2. 18.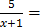 
10
Solution
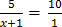
5 x 1 = 10 (x + 1)
5 = 10x + 10
5 – 10 = 10x
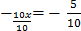
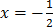
19. 
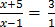
solution
1 (x + 5) = 3 (x – 1)
x+ 5 = 3x – 3
3 + 5 = 3x – x
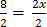
∴ x = 4
20. 
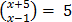
Solution
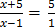
1 (x + 5) = 5 (x – 1)
x + 5 = 5x – 5
5 + 5 = 5x – x
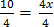
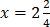
Solving word problems
E.g. 1
If John has hundred shillings, how many oranges can be buy if orange costs 50 shillings?
Solution
Let k be the number of oranges John can buy but one orange costs 50shs.
50 x k = 200
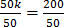
K = 4
∴John can buy 4 oranges
Example 2:
A father age is 4 times the age of his son. If the sum of there is fifty years Find the age of the son.
Solution
Let the age of father be y
Let the age of the son be x
Therefore the age of the father is y = 4x
Their sum = 4x + x = 50
5x = 50
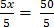
∴The son’s age is 10years old
Example 3:
The sum of 2 consecutive numbers is 31. Find the smaller numbers
Solution
Let the smaller number be x
Let the bigger number be x + 1
x+ x + 1 = 31
2x + 1 = 31
2x = 31 – 1
2x = 30
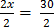
∴ The smaller number is 15
Exercise 7.5
1. If 4 is added to a number and the sum is multiplied by 3 the result is 27. Find the number.
Solution
Let the number be ‘b’
(b + 4) x 3 = 27
12 + 3b = 27
3b = 15
b= 5
2. Okwi’s age is six times uli’s age.15 years hence Okwi will be three times as old as Uli. Find their ages.
Solution
Let the age of Uli be x
Okwi = 6x
Okwi Uli
6x x
6x + 15 x + 5
6x + 15 = 3x + 45
fifteen years to come
6x + 15 15 + x
Then 6x + 15 = 3(x + 15)
6x + 15 = 3x + 45
6x – 3x = 45 – 15
3x = 30
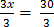
x = 10
Okwi = 60 years
Uli = 10 years
3 . The sum of two consecutive odd numbers is 88. Find the numbers
Solution
Let the number be n
n + 2, n + 4
n + 2 + n + 4 = 88
2n + 6 = 88
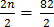
n = 41
The smaller number = 41 + 2 = 43
The bigger number = 41 + 4 = 45
4. Obi’s age is twice Oba’s age. 4 years ago Obi was three times as old as Oba. Find their ages.
Solution
Oba’s age let it be x
Obi Oba
2x x
2x – 4 x – 4
2x – 4 = (x – 4) 3
2x – 4 = 3x – 12
8 = x
Obi = 16 years old.
Oba = 8 years old.
Inequalities in one unknown
The following rules are useful when solving inequalities
i) Adding or subtracting equal amounts from each side does not change the inequalities sign
Example : solve x – 2 ≤ 4
Solution
X – 2 + 2 ≤ 4 + 2
X ≤ 6
Example 2: 2x + 4 ≥ 16
Solution
2x + 4 – 4 ≥ 16 – 4
≥ 
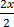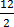
X ≥ 6
ii) Multiplying or dividing by same positive number each side change the inequality sign
Example: solve 3y + 16 < 50
Solution
3y + 16 – 16 < 50 – 16
,
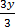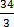
Example 2:
(2x – 4) ≥ 9
(2x – 4) ≥ 9 x 3
2x – 4 + 4 ≥ 29 x 3
≥ 
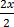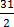
X ≥ 3
iii) Multiplying or dividing each side by negative number CHANGES the inequality sign.
Example. Solve the inequality
(
(4 – 3x) < 4
Solution
2 (4 – 3x) < 4 x 3
2 (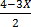
) < 
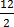
4 – 3x < 6
-3x < 6 – 4
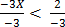
The sign changes
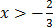
Examples 1: Solve -4x + 3≥
-4x + 3≥ 
-4x ≥ 
-3
-4x ≥ –
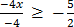÷ -4
x ≤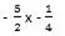 
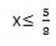
Examples 2. solve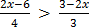 
Find their L.C.M
3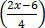 
> 
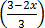x 4
3 (2x – 6) 4 (3 – 2x)
6x – 18 > 12 – 8x
6x + 8x > 12 + 18
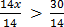
X >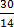 
BINARY OPERATIONS
Is an operation denoted by *, which describe the formula of a given variables.
if P * q = 5pq – p: Find
i) 2 * 3 =
p = 2 and q = 3
2 * 3 = 5 (2) (3) – 2
= 30 – 2 = 28
2 * 3 = 28
ii) (1* 2) * 3
Solution
(1 * 2) = p = 1 and q = 2
In (1 * 2) = 5 (1) (2) -1 = 9
=10-1
=9
∴1∗2=9
9 * 3 = p * q
9 * 3 = 5 (9) (3) – 9
= 135 – 9
= 126
(1 * 2) * 3 = 126
iv) (2 * 1) * (3 * 2)
Solution
2 * 1 = p = 2 and q = 1
5 (2) (1) – 2
2 * 1 = 10 – 2
= 8
3 * 2 = p = 3 and q = 2
5 (3) (2) – 3
15 x 2 – 3
3 * 2 = 30 – 3
3∗2= 27
2 * 1 = 8
3 * 2 = 27
8 * 27
8 * 27 = p = 8 and q = 27
5 (8) (27) – 8
40 x 27 – 8
1080 – 8
Then: 8 * 27 = 1072
(2 * 1) * (3 8 2) = 1072
iv. if (t * 5) = 50 find t
Solution
t * 5 = p = t and q = 5
t * 5 = 5 (t) (5) – t
15t – t
24t=50
t * 5 = 24t
= 
= 
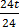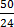
t = 
