ARITHMETIC SERIES
Is a series in which the difference between consecutive terms is the same.
The difference between the consecutive terms is known as the common difference
The nth term of the arithmetic series is given by
An = A1 + [n-1] d
An = the nth term
A 1 = the 1st term
n = is the number of terms
d = is the common difference
Example
Determine 12th term and 32nd term of the series
3+6+9……………
Solution
An = A 1+ [n-1] d
A12 = 3+ [12-1] 3
A12 = 3+ [11 x 3]
A12= 3+33
A 12 = 36
The 12th term is 36
An = A1+ [n-1] d
A 32=3 + [31 x 3]
A 32 = 3 +93
A 32 = 96
The 6th term of an arithmetic series is 18 and the 10th term is 30 determine the common difference
Solution
A6 = A1 +5d = 18…………. i
A10= A1 + 9d =30………..ii
From {i}
A 1 = 18-5d ….. [iii]
iii] Into [ii]
18-5d +9d = 30
8+4d=30
 =
= 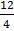
d = 3
Common difference = 3
Solution
From [iii]
A 1= 18-5[-5[3]
A 1 =18-15
A 1 =3
First term = 3
The sum of the first n- terms of an arithmetic progression
The sum of the first n terms of AP is given by
S n = n/2 [A1 +An] ….. (i)
Where
n = number of terms
An = nth term
Sn = sum of n term
But An = A1 + [n -1] d ………. [ii
Sn = n/2 [ A1 + A1 + [ n -1] d
= n/2 [ 2A1 + [ n -1] d ……….. iii]
Examples
1) The sum of 18 terms is 812 if the common difference is 7 find the first term
2) Find the sum of the first 35 terms of the series
3+7+11+15+…………
Solution
Sn = n/2 [2A1+ [n-1] d]
S 18 = [18/2(2A1+ [18-1)7]
S 18 = 9 [2A1+ [17×7]
S 18= 9 [2A1 +119]
812 = 18A1 + 1071
18A1= 1071-812
18A1= 259
A 1= 14.4
The first term is 14.4
Solution [ii]
Sn = n/2 [2A1 + [n -1] d]
S35 = 35/2 [2[3] + [35-1] 4
S 35= 17.5 [6+[ 34 x 4]
S 35= 17.5 [6+136]
S35 = 17.5 [142]
S 35 = 2485
The sum of the first 35 term is 2485
Exercise
i) Find the 25th term of the series
3+9+15+……….
ii) The 6th term of the series is 33 and the 11th term is 48
Determine the 45th term of the AP series
iii) The first term of A.P is 31/3 and the 9th term is 23 find the 44th term
iv) The last term of the AP is 204 the common difference is 3 and the first term is 3 and the first term is 3 find the number of terms
v) Find the sum of series
3+6+9…………. +204
Missing notes of Geometric, (G.P)
EXERCISE
1) If the 4th term of a G.P is 9 and the 6th term is 81 find
a) The common ratio
b) The first term
2) The nth term of the G.P
4, 8 , 16 , ………… is 1024 find n.
3) Find the 9th term of the G.P
2, -6, 18, -54, ……………
4) The 3rd term of the GP is 10 and the 6th term is 80. find ;
a) The common ratio
b) The first term
5) If a GP is given by Gn = 3n find the sum of the first eight terms
6) Find the sum of the first twelve terms of the GP
2, -6, 18, -54
7) In a G.P the 11th term is 128 times the 4th term and the sum of the 2nd and 3rd term is 6, determine
a) The common ratio
b) The first term
c) The sum of the first 5 terms
d) The sum of the 3rd to 6th terms inclusive
8)Find the sum to infinite of the series
-1/3 + 1/9- 1/27………….
16+16/3+ 16/9……………
2/3+ 4/4 + 8/27…………….
9)Express the following repeating decimal as a fraction
a) 0.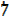
b) 0.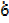
c) 0.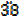
d) 2.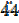
e) 3.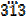
Solution
1) a) Common ratio = 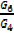
r = 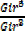
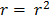
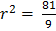

r =3
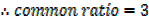
c) G 4 = G1r(4-1)
9 = G1r 3
9= G1r3
9 = G1 27
G1 = 9/27
G1 = 0.3
2) 4, 8, 16,…………… 1024
Given, Gn = 1024,G1= 4,r=2
Using
Gn=G1rn-1
required to find the number of terms, n
Gn=G1rn-1
1024 =(4)(2)n-1
256 =2n-1
28=2n-1
Equating their powers
8=n-1
n=9
3)Gn=G1rn-1
G9 =(2)(-3)(9-1)
G9 =(2)(-3)8
G9 =2(6561)
G9 =13122