RATIOS AND VARIATIONS
RATIO
Is the comparison of two quantities with the same unit.The ratio is related with fractions
For example
a/b can be written as a: b
Examples
1. Form four class has got 40girls and 30 boys what is the ratio of boys to that of girls?
2. The area of a circle and its radius are in a ratio of 22:1 if the area is 154 cm2
find the circumference of the circle
Solution
1. Let” b ” be the number of boys and ”g” be the number of girls
b: g = 30:40
∴ b : g = 3:4
Solutions
2) Let ‘a’ be the area of the circle ”r ”be the radius of the circle
Then
a:r =22:1
= 
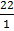
154cm2 = 22
r =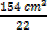 
r = 7cm
Circumference of the circle = 2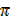 
r
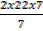
The circumference is 44cm
Proportions
When two ratios are compared by using equal signs it is called proportions i.e. you may have two ratios may be a : b = c : d
Example
(i) The ratio of boys to girls at Jitahidi sec. school is 3:4 if the school has 60 boys find
a) → The number of girls
b) →The total number of students
ii) Divide Tshs 360,000 in the ratio 2:3:5
Solution
(i)Let ”n” be the number of girls at Jitahidi and “a” be the number of boys
a: n = 3:4
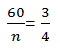
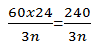
n = 80
Therefore the number of girls = 80
Total number of students [60+80] = 140
(ii)2+3+5 =10
2/10 x 360,000 = 720,00
3/10 x 360,000= 108,000
5/10 x 360,= 180,000
DIRECT PROPORTIONS
When one variable increases the other variable also increases and vice versa.
i .e y∝x
y = kx
Where k is proportionality constant
Example
If y = 9 when x =3 find the value of x when y = ¼ given that y is directly proportional to x
Solution
y∝x
If y=9, then x=3,
y=3x
Given
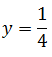
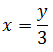
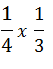
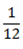
INVERSE PROPORTIONS
When one variable increases the other variable decreases and vice versa
i.e
y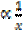 
y = k/x
Example
10 men take 12 days to cultivate the farm how long could it take for 15 men to cultivate the same farm?
Let ”f”’ be the number of men and ”g” be the number of days.
g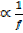 
g =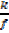 
12 =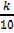 
k = 120
If f =15,
g = 8
For 15 men the farm will be cultivated by 8 days
JOINT VARIATION
Is the variation where by one quantity depends on two or more quantities
For example
If P varies directly with x and inversely with y
Then
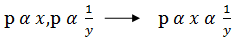
P 
P = kx /y
Example
If z varies inversely as y and directly as x3 determine z in terms of x and y given that z = 3, x = 2 and y = 3
Solution
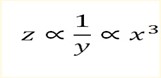or z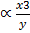
z =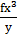 
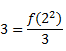
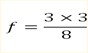
f = 9/8
∴z =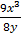 
Exercise
1. Mr Othman divided 30 books to his children Khadija , Omary and Hafsa in the ratio 1:2:2 what was the share of each of the three children
2. Given that 2x2-3xy+y=0 is an implicit equation determine the possible ratio of x to y
3. Abubakar is 1.5 times as tall as Omar if Omar is 90cm tall, find the height of Abubakar
4. Given that the ratios of x and y [ x:y] = -4 and x:y = 3 are two ratios obtained from the same implicit equation, determine the equation
5. A varies inversely as r2 if A=1 where r=1 find
a.) A in terms of r
b.) A when r = 7
6. X varies directly as y and x = 4 when y = 100 find y when x = 60
7. If x varies inversely as y2 and x = 8 when y = 3
a.) Express x in terms of y
b.) Find x when y = 4 and y when x = 4
8. Given that t = √3 when z = 9. Find the formula which satisfies the following
a.) T2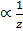
b.) T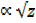 
c.)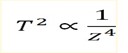 
d.) T ∝ z2
9. If m varies inversely as n and directly as r4 determine m in terms of n and r given that m =2, n = 1 and r =4.
Solutions
1) 1+2+2 = 5
1/5 x30 = 6
1/5 x30=12
2/5 x 30 =12
Khadija will get 6 books
∴Omari will get 12 books
∴Hafsa will get 12 books
Split the middle term
2x2-3xy +y2 = 0
[x-y][2x-y] = 0
Either
[x-y] = 0 or [2x-y] =0
x=y or 2x = y