Is the process of rounding off a number in the given places in rounding makes numbers easier to deal with but at the same time reduces their accuracy.
The methods used for approximation or rounding off numbers are decimal places and significant figures.
ROUNDING OFF PROCEDURES
i) If the first neglected digit is greater or equal to 5 the digit occupying the place value will increase by 1 unit
ii) If the first neglected number is less than five, then the number occupying the required place value will remain unchanged.
ROUNDING OFF NUMBERS
Examples
1. Round off the following numbers to the nearest whole number.
a) 3425
b) 7.283
c) 6.674
d) 0.625
e) 36.12
f) 5446
Solutions
a) 3425≈ 3000
b) 7.283≈7
c) 6.674≈7
d) 0.625≈1
e) 36.12≈36
f) 5446≈5000
2. Round off the following to
a) 1 decimal place.
b) 2 decimal places.
c) 3 decimal places.
a) 23.7016
b) 0.0094
Solution
- 23.7016≈23.7 to 1 decimal place.
- 23.7016≈23.70 to 2 decimal place.
- 23.7016≈23.702 to 3 decimal places.
edu.uptymez.com
b) 0.0094
a) 0.0094≈0.0 to 1 decimal place.
b) 0.0094≈0.001 to 2 decimal place.
c) 0.0094≈0.009 to 3 decimal places.
3. Round off the following number to the nearest
a) Whole number
b) Tenth
c) Hundredth
i. 0.625
ii. 8.385
Solution
i. 0.625
a) 0.625≈1 to whole numbers
b) 0.625≈0.6 to tenth
c) 0.625≈0.63 to hundredths
ii. 8.385
a) 8.385≈8 to whole numbers
b) 8.385≈8.4 to tenth
c) 8.385≈ 8.39 to hundredths
Example: Round off 84678 to
i) Tens
Solution
84678 = 84700
ii) Hundreds
Solution
84678 = 85000
iii) Thousands
Solution
84678 = 80000
Example: Round off 179999 correct to i) hundreds ii) Thousand iii) Tens iv )Ten thousands
Solution
i) 179999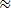
180000
ii) 180000
iii) 180000
iv) 180000
Significant Figures
The are the total number of digits in the given number including zero’s which are in between non-zero digits.
Note
i) Zero is a significant figure when is in between two non – zero digits
ii) When zero is an outcome of approximation (rounding off) where a 9 receives l and becomes ten, then zero of ten is a significant figure.
Examples: determine the number of significant figures in the following
i) 20896100
= There are six significant figures
ii) 0.00025060
= There are four significant figures
iii) 2.00008453
= There are nine significant figures
Examples: Re write following numbers correcting to the required of significant figures.
a. 0.23678 to 3 significant figures
Solution
0.23678
∴= 0.24
b. 2.09478 to 3 significant figures
Solution
2.09478
∴= 2.09
c. 0.009994 to 2 significant figures
Solution
0.009994
∴= 0.010
d. 0.00931225697 to 7significant figures
Solutions
0.00931225697
∴= 0.0093123
Exercise
Re write the following numbers correctly to
a. 10.999009 to three significant figures
Solution
10.999009
∴= 11.0
b. 705.4005 to six significant figures
Solution
705.4005
= 705.401
C. 847910 to three significant figures
Solution
847910
∴= 848000
Approximations in operations
When you want to check approximation whether a calculation is correct or not. Round each number in the calculation to 1 significant figure. Do the calculation mentally.
Example:
A group of 42 people go to the cinema, which cost 680/- each. What is the approximation total cost?
Solution
Round 42 to 40 and 680 to 700
Therefore 40 x 700 = 28,000/=
Note: The exact cost is 28,560 The approximation is 28,000 which is close.
