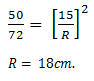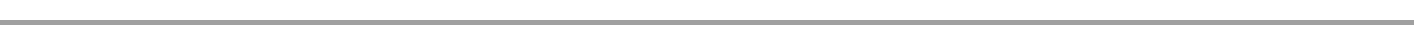AREAS
CASE
1.Right angled triangle Area = ½ b x h
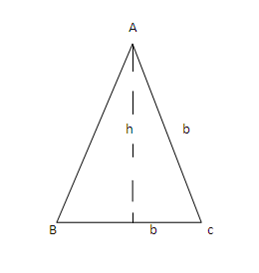
2. Triangle with altitude that lies within the triangle
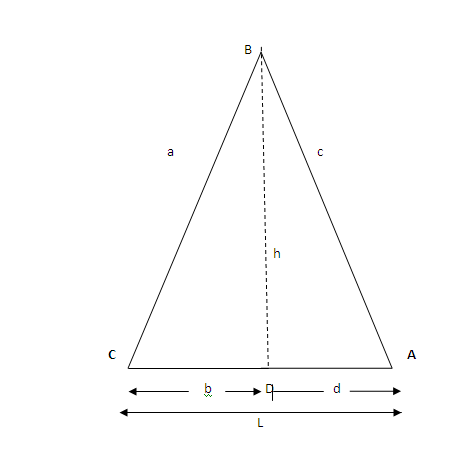
Area 0f Δ ABC = ½ bh + ½ d h
= ½ h(b + d)
= ½ hL
3. A triangle where the altitude of triangle lies outside of the triangle.
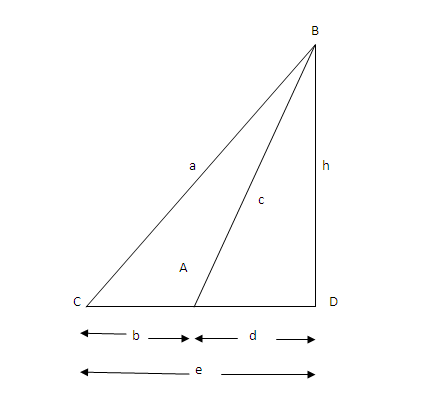
Area of ABC = area of triangle BCD – area of triangle ABD
= ½ h (b+d) – ½ h d
= ½ h e – ½ h d
= ½ h (e-d)
In all the triangle the formula is the same.
Thus if you were given a triangle with a base b and its corresponding height (altitude) h, its area is equal to ½ b h
CASE II
We can also use the knowledge of trigonometrical ratios.
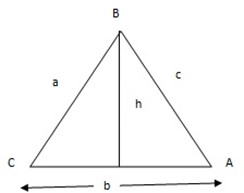
Area of triangle ABC = ½ b h
= ½ b a sin c
Sin A = h/c
h= c sin A
the area of triangle ABC = ½ b c sin A
Example
1. The length of two sides of a triangle are 8cm and 10 cm. find he area of the triangle, if the included angle is 30 0.
Solution;
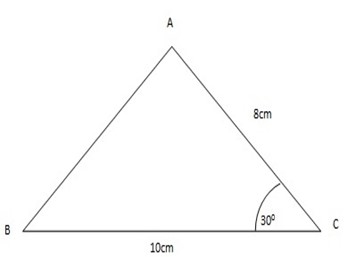
Area = ½ x 10 x 8 x sin 300
= 40 x ½Cm2
=20cm2
2. The area of triangle ABC with sides a,b,c.
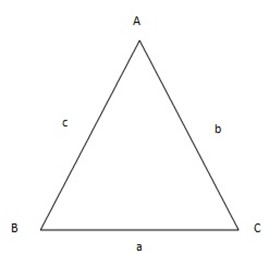
Area of triangle ABC
= ½ c b sin A
= ½ a c sin B
= ½ a b sin C
Example
The base of triangle PQR is 17 cm long. If corresponding height is 20cm, find the area of the triangle.
Solution;
Area of triangle PQR = ½ b h
= ½ x 17 x 20
= 170 cm2
Qn. 9
what is the area of the paper required to make the kite shown in the figure
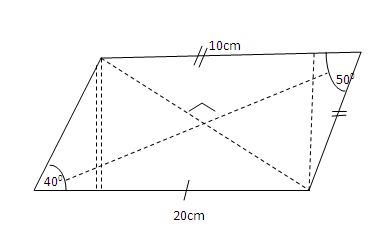
Solution
(i) = ½ x 20 x 20 x sin 40º
= 200 x 0.6428
=128.56cm2
(ii)= ½ x 10 x 10 x sin 500
= 50 x 0.7660
= 38.3 cm2
AREA OF TRAPEZIUM
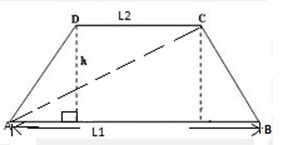
Area of trapezium ABCD = area of triangle ABC + area required of triangle ADC
= 
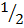L 1 h + 
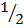L2 h
= 
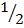h(L1 + L2)
Examples.
1. Calculate the height of trapezium with area 84 square units and bases 16 units and 8 units as shown ;
Area = ½ h ( b1+ b2)
84 = ½ h ( 16+ 8)
84 = 12 h
h = 7 units.
AREA OF PARALLELOGRAM
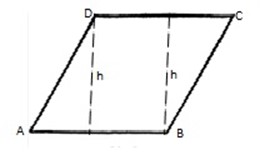
Area of parallelogram ABCD = area of ΔABD + ΔBCD
= ½ A B h + ½ C D h
= ½ h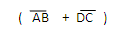 
= ½ h 
= h x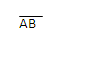 
Area of parallelogram = bh
AREA OF RHOMBUS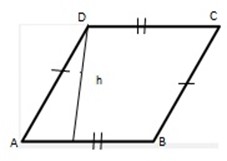
A rhombus is also a parallelogram.
Area = bh
We can also find the area of the rhombus by considering the diagonals of a rhombus.
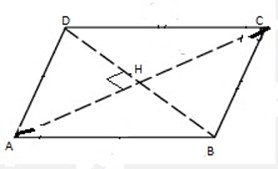
AC and DB are the diagonals.
Area of triangle ABC = area of triangle ADC
Area of rhombus ABCD= 2 (area of triangle ABC)
OR = 2 ( area of triangle ADC)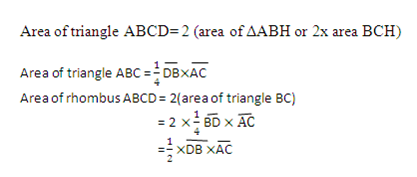
EXERCISE
1. 1. Calculate the area of a rhombus whose diagonals are 12dm and 10 dm.
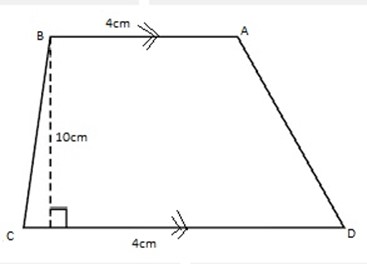
2. 2. Calculate the area of the trapezium ABCD shown in the figure below
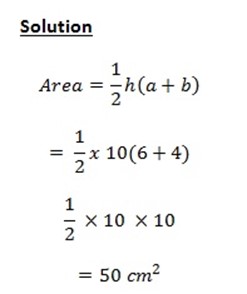
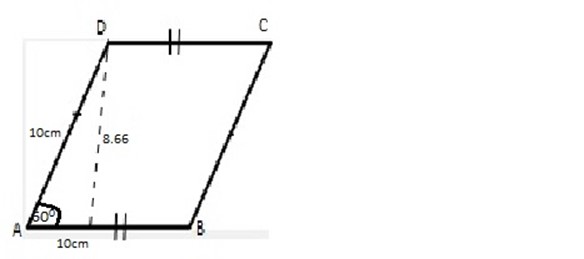
3. ABCD is a parallelogram with A= 10cm, BAD = 600. Calculate the area of the parallelogram.
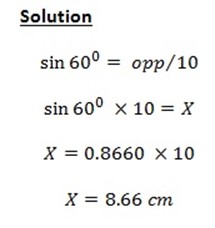
4. 4. Find the area of trapezium ABCD shown in the figure below;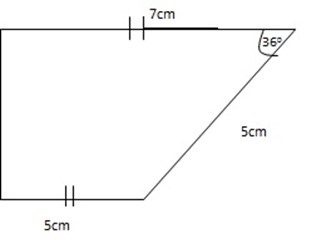
Sin 360 = h/ s
Solution4:
h = 0.5878x 5 cm
h= 2.939 cm
area = ½ x 2.939 (7+5)
= ½ x 2.939(12)
= 17.634cm2
AREA OF A RECTANGLE
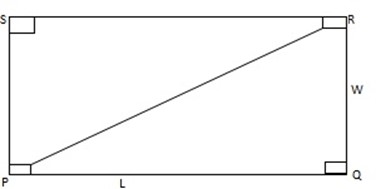
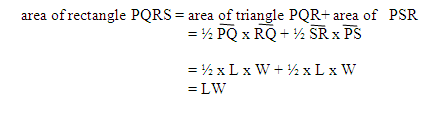
AREA OF SQUARE
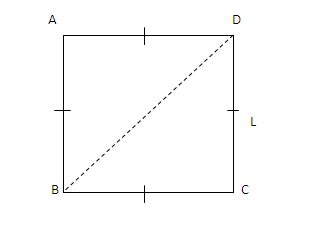
A square is a rectangle with equal sides.
Area of triangle ABC = area of triangle ADC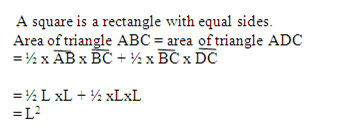
Also we can find the area of a square by considering the diagonals.
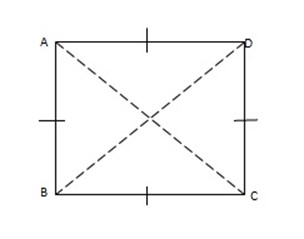
ΔABC = ΔADC
Area of triangle ABC = Area of triangle ADC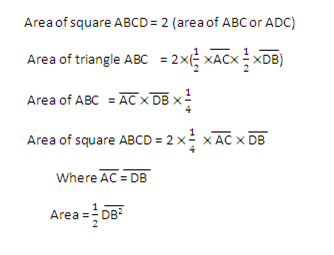
Example
1. Find the area of square in which diagonals have length of 12.5cm2
Solution
Area = ½ (length of diagonals)2
= ½ (12.5) 2
= 78.125cm 2
TOTAL SURFACE AREA OF A RIGHT CIRCULAR CONE
Right circular cone Is the one whose vertex is vertically above the center of the base of the cone.
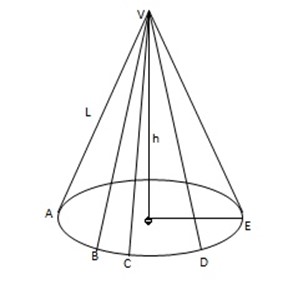
Total surface area of a cone = area of curved surface + base area.
BUT;
area of curved surface ( lateral surface ) = area of small triangles.
If we consider our cone , AB, BC , CD and DC are approximated line segments, hence we have small triangles VAB,VBC , VCD and VDE.
Hence area of curved surface
= ½ AB x VA + ½ BC x VC + ½ CD x VC + ½ DEx VD
But VA= VB = VC = VD = VE
Area of curved surface = ½ AxBxL+ ½ BxCxL+ ½ xCx DxL+ ½ DxExL
= ½ L (AB+BC+CD+DE)
= ½ L (2πR)
= πRL
Total surface area = πR2+ πRL
= πR(R+L)
TOTAL SURFACE AREA OF A RIGHT CYLINDER
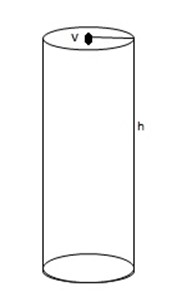
Total surface area of a right cylinder
= area of curved surface+ bases area.
= 2πRh + πR2
TOTAL SURFACE AREA OF A RIGHT PYRAMID
A right pyramid is the one which the slant edges joining the vertex to the corner of the base are equal.
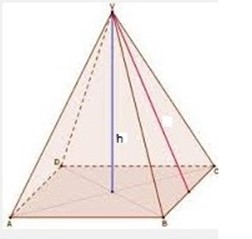
Total surface area of a right pyramid
=area of triangle VAB+ VBC+VDC+VDA + area of the base.
= lateral surface + area of the base.
BUT
As VAB, VDC, VBC and VDA are isosceles triangles. Then VA,VB,VC and VD are slant height.
Example
Consider the data below of a right pyramid. Find the total surface area of the pyramid.
Total surface area of a pyramid
= area of laterals + base area
=area of ΔVAB+ ΔVBC+ ΔVDC+ ΔVDA+ base area
EXERCISE
1. The radius of a base of right circular cylinder is 7dm and height is 10 dm. find;
(a). The total surface area.
Solution:
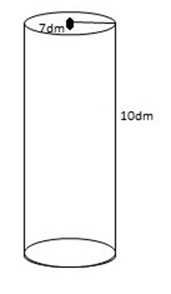
The total surface area = 2πR (h+r)
= 2 x 3.14 x 7 dm (10+7)
= 74.732 dm2
2. Calculate the lateral surface area of the right cone shown below.
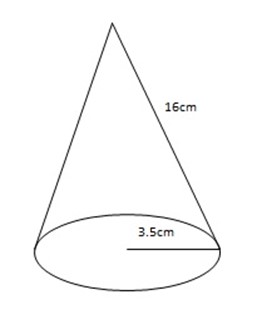
= πr(r+L)
= 3.14×3.5x(3.5+1.6)
= 3.14×3.5×19.5
= 214.305cm2
THE TOTAL SURFACE AREA OF A RIGHT PRISM
A right prism is a prism in which each of the vertical edges is perpendicular to the plane of the base. an example of right prism is shown in the figure below where EABF, FBSG, HDCG and EADH are faces made up the lateral surface. and ABCD and EFGH are bases.
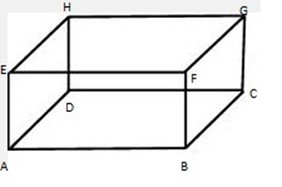
A right prism is a prism in which each of the vertical edges is perpendicular to the plane of the base. an example of right prism is shown in the figure below where EABF, FBSG, HDCG and EADH are faces made up the lateral surface. and EFGH are bases.
The total surface area of a prism ABCDEFG
= Area of lateral surface + base area
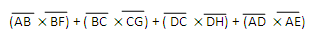
Example
Find the total surface area of a rectangular prism 12cm long,8 cm wide, and 5 cm high.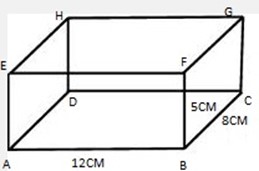
soln
Surface Area = BF(ABxBC)2
=5( 12 x8) 2
= 5cm x 192cm
=960 cm2
Base area = 12×8 x2
= 192 cm2 . : Total surface area = 240 cm2 +192 cm2 = 432 cm2
Exercise
1. The altitude of a rectangular prism is 4cm and the width and length of its base are 12cm and 3 cm respectively. Calculate the total surface area of the prism.
2. One side of a cube is 4dm. calculate
a. The lateral surface area.
b. Total surface area.
3. Figure below shows a right triangular prism whose base is a right angles triangle. Calculate its total surface area.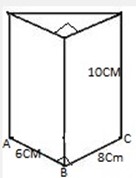
4. The altitude of a square pyramid is 5units long and a side of the base is 5 units long. Find the area of a horizontal cross-section at distance 2 units above the base.
Solution
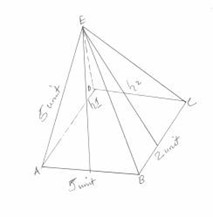
Answers
Solution1(a)
= 4(2+3) 2 +2(2×3)
= 4×10 + 12
= 40 + 12
= 53cm2
Solution2.
(a) Lateral area = 2 (4+4+4+4)
=2x 16
=32dm2
(b)Total surface area = 32 + 2(4+4)
= 48 dm2
Solution3.
=(AB2) + (BC2) = ( AC2)
=62 + 82 = AC2
AC=10
= 8x10cm2= 80 cm2
Area of triangle = ½ b h
= ½ x 6 x 8 x 2
= 48cm2
Area of rectangle b = 10cmx10cm
=100cm2
Total surface area = 100cm2 + 48 cm2+ 80cm2
=228cm2
Solution4.
a2+b2=c2
2.52+ b2= 52
b2= 25-6.25
b= 4.33=h
a2+b2=c2
a2=251
A1= (½ x 5×4.33) x2
=21.65cm2
A2= x 2 x4.89×2
A2= 9.798
Area = 9.798+21.65 cm2
=31.448cm2
AREA OF A CIRCLE
Consider a circle with several radii (r).
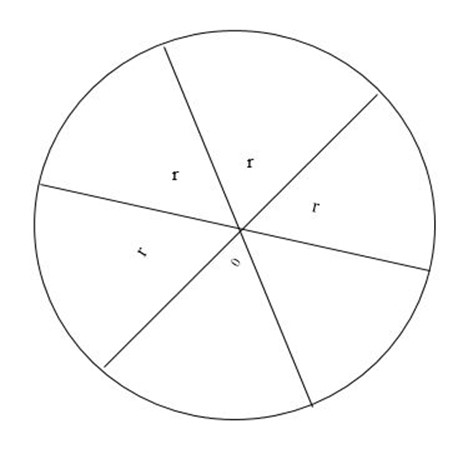
Re-arrange those pieces from a circle to form a parallelogram.
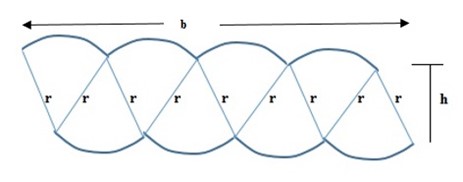
A= bh
= ½ c r
½ c r = 2πr
Area of a circle = πr2
Area of a sphere = 4 πr2
LENGTH AND PERIMETER OF A RECTANGULAR POLYGON INSCRIBED IN A CIRCLE.
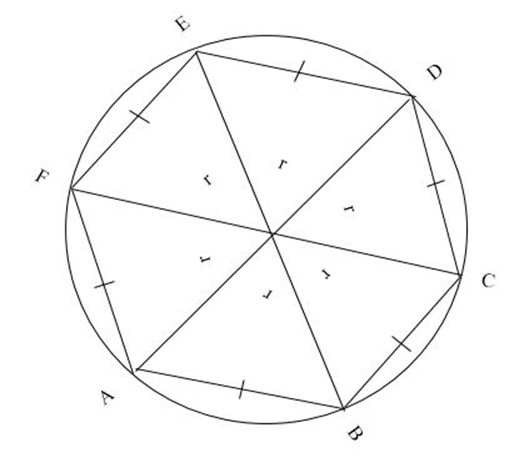
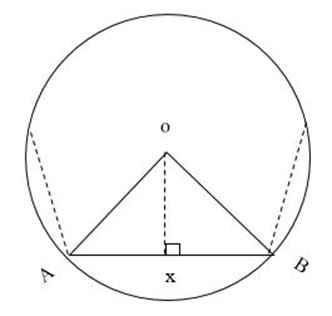
Consider triangle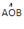 
AO is perpendicular to AB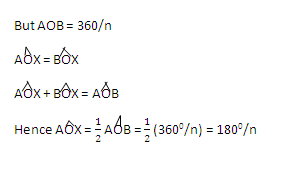
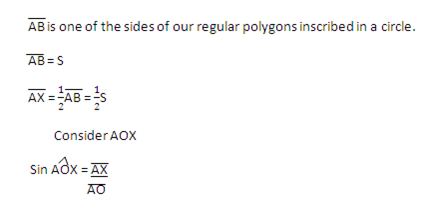
Sin 1800 /n =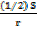 
s=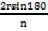 
s=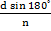 
p=ns
p= n(dsin180Ëš)
AREA OF A RECTANGULAR POLYGON INSCRIBED IN A CIRCLE
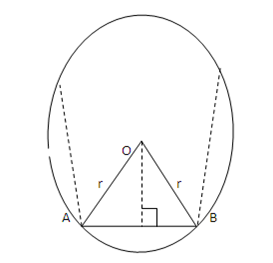
Area of a ΔAOB =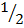 
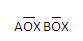sinY
AOB =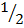 
r x r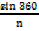 
Area of regular polygon inscribed in a circle.= n (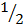
r2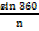 
)
Exercise
1. Find the length of one side of a regular nine –sided polygon inscribed in a circle of radius 10 cm2.
2. Find the radius of a circle which inscribes an equilateral triangle with perimeter 24 cm.
3. Find the area of a 9-sided polygon inscribed in a circle with radius 5 cm.
4.Find the area between two concentric circles.
Answers
Solution 1.
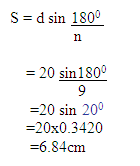
Solution2.
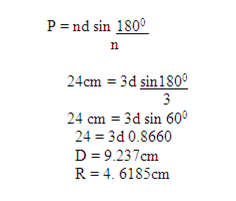
Solution3.
Area =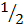 
n r2 sin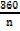 
= ½ x9 x 25 x sin 40 0
=11.25 x 0.6428
=72.315cm2
Solution4.
Area = πr2
= 3.14 x6x6
=113.04 cm2
Area = πr2
=3.14x 4×4
=50.24cm2
Area between circles = 113.04cm2 – 50.24cm2
=62.80cm2
AREAS OF SIMILAR FIGURES
Similarity
Two polygons are similar when their corresponding angles are equal and corresponding sides are proportional.
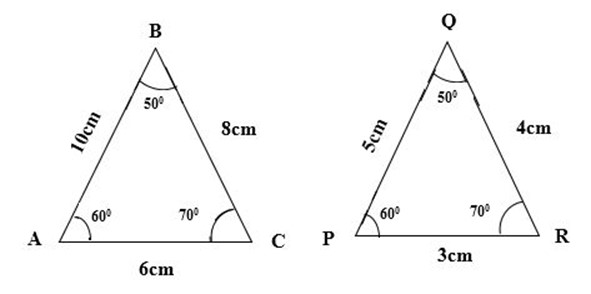
Similarity of polygons
If corresponding angles are equal, also if the corresponding side are proportional.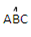
=
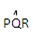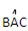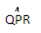= 500
= 
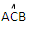= 600
= 
= 70 0
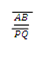= 10cm = 2
5cm
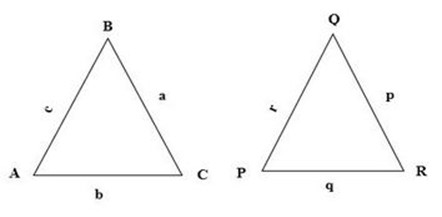
Area of triangle ABC = ½x a x c sin B
Area of triangle PQR = ½ r p sin Q
Area of triangle ABC = ½ ac sin B
Area of triangle PQR ½ r p sin Q
But Sin B = sin Q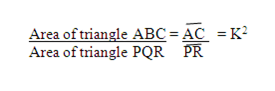
Exercise.
1. Two triangles are similar, A side is 6cm long. The corresponding side to the other is 20cm. if the area of the first is 90 cm2 . what is the area of the second?
2. The ratios of the areas of two circles is 50: 72. If the radius of the smaller circle is 15 cm, find the radius of the larger circle
3. Two triangles are similar. A side of one is 2 units long . the corresponding side of the other is 5 units long. What is the ratio of their areas?
5. Two polygons are similar. A side of one is 8 cm long . the corresponding side of the other is18 cm . the area of the first is 16cm2. Find the area of the second.
6. The ratio of the area of two circles is 50: 72. If the radius of the smaller circle is 15 cm, find the radius of the larger circle.
Answers
Solution1.
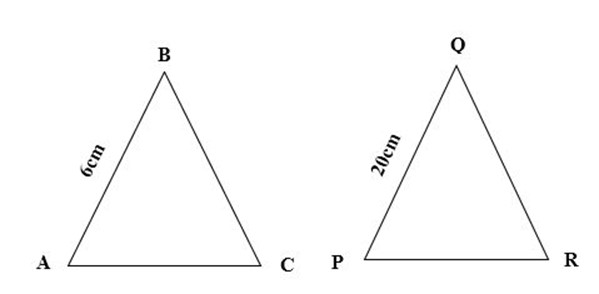
Area of triangle ABC = K2
Area of triangle PQR
Where K = 6/20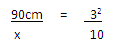
X=100cm2
90cm = 3 2
X 10
Solution 2
Area of small circle = K2
Area of large circle
Where K = 15/X
50 = 152
72 X
X=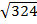 
X = 18cm
Solution 3.
Area of triangle 1 = K2
Area of triangle 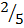2
= (
)2
= 
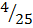
Areas = 4:25
Solution4.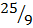
= K2
K =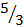 
The ratio of corresponding sides = 5:4.
Solution5.
Area of triangle 1 = K 2
Area of triangle 2
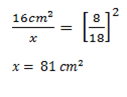
Solution6.
Area of small circle = K 2
Area of big circle
