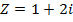ADVANCED MATHEMATICS FORM 6 – COMPLEX NUMBER

GRAPHICAL ADDITION AND SUBTRACTION

Consider Z and Z₂ representing an Argand diagram

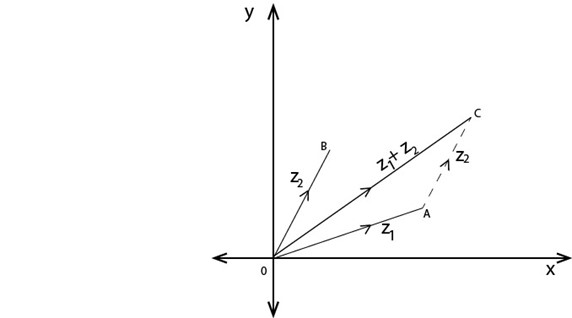
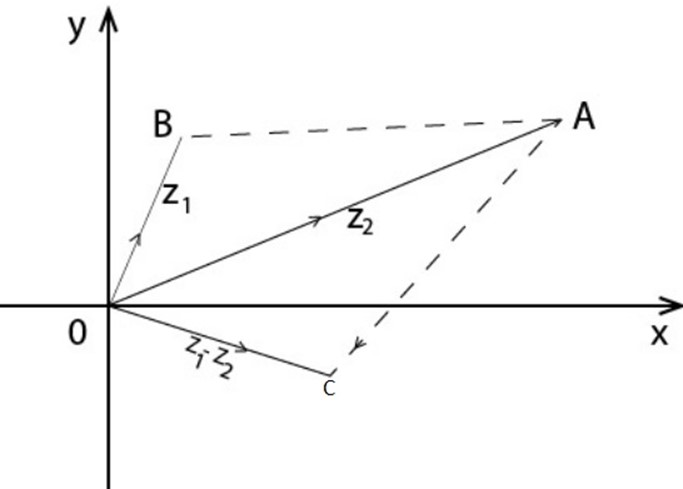
Taking 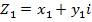 and 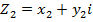 .The coordinates of C are

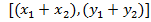
Hence 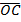 represented the complex number
 .

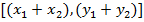MODULUS AND ARGUMENT

Let 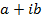 be the complex number which suggests that  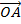represents  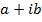and A (a, b) is the point

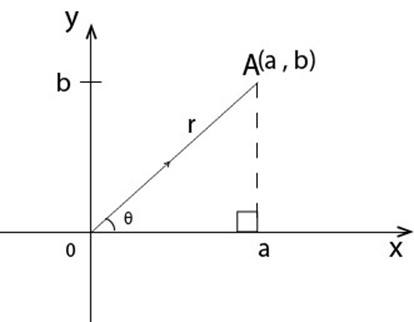
r is the length of OA

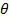 Is the angle between the positive x axis and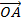

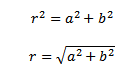
OA is called the modulus of complex number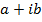

i.e.

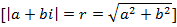
The angle 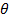 is called the argument of  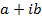and written arg()

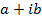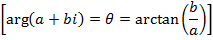
Note:

The position of OA is unique and corresponds to only one value of 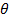 in the range

An argument is also known as amplitude

–      To find the argument of  we use  together with quadrant diagram

Example

Find the argument of each of the following complex numbers

a)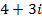 

b)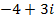 

c)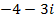 

d)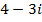

Solution
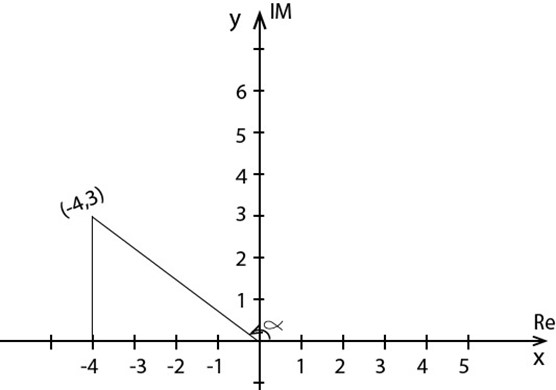
(a) 4+3i

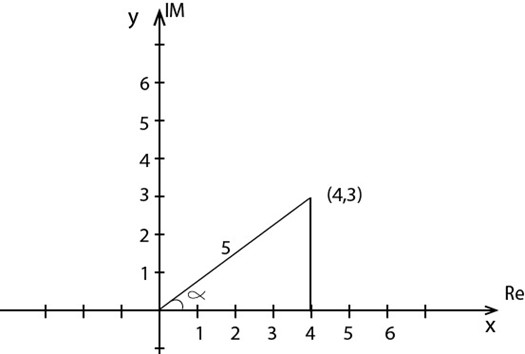
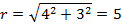
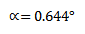
Solution
(b)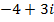

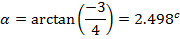
Solution
(c)-4-3i

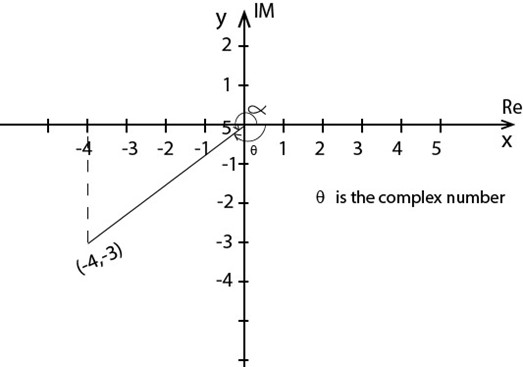
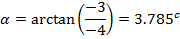
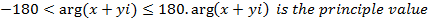
Solution
(d)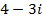

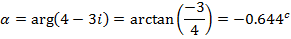
EXERCISE

Represent the following complex numbers by lines on Argand diagrams. Determine the modulus and argument of each complex number

a)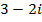

b)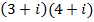

SQUARE ROOTS OF COMPLEX NUMBERS

Example

Find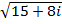   

Solution

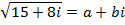
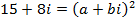
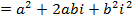
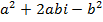
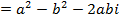
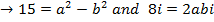
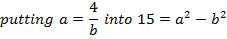
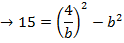
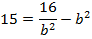
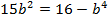
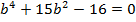
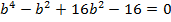
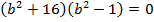
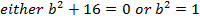
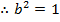
Example;

Given that is a root of the equation 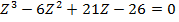 find the other two roots

Solution

Polynomial has real coefficient  and its conjugate is a root of the polynomial

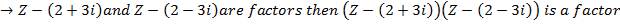
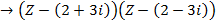
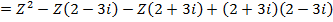
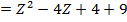
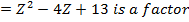
⇒To find the other factor of z³ – 6z² + 21z – 26 =0

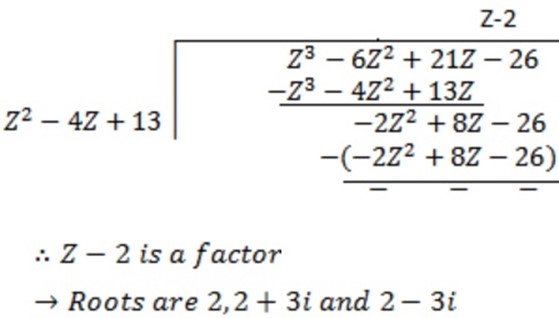
EXERCISE

1. Solve the following equation

2. Given that 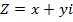  express the complex number  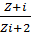 in polynomial form hence find resulting complex when