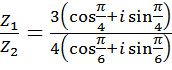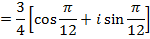ADVANCED MATHEMATICS FORM 6 – COMPLEX NUMBER

POLAR FORM OF A COMPLEX NUMBER

If  then Z can be written in polar form i.e. in terms r and

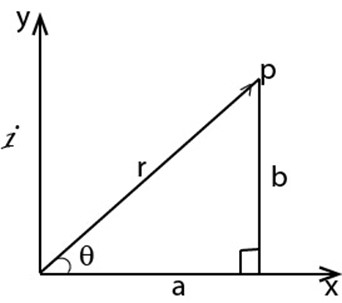
Let OP be a vector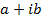
r be the length of the vector

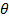        be the angle made with OX

From the diagram (Argand diagram) we can see that

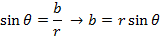
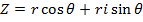
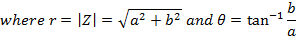
Example

Express 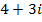 in polar form

Solution

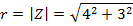
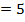
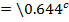
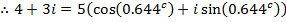
NOTE

If the argument is greater than 90, care must be taken in evaluating the cosine and sine to include the appropriate signs.

E.g.

Express in the form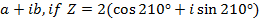

Solution

Since the vector lies in the 3^rd quadrant

i.e.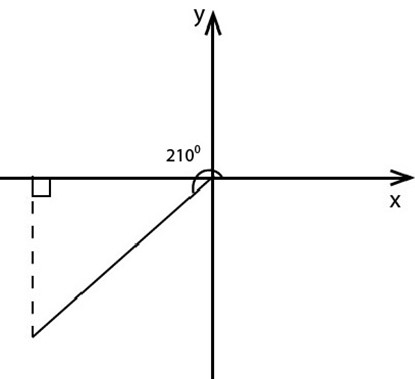

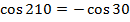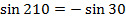â—¦
â—¦

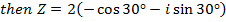
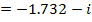
CONJUGATES IN POLAR FORM

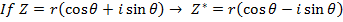
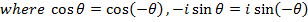
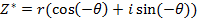
NB:

Taking the conjugate in polar form changes the sign of its argument

Example

Express 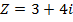 in polar form and then find its conjugate

Solution

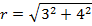
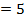
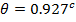
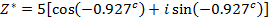
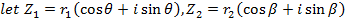
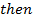
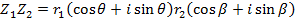
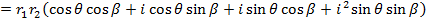
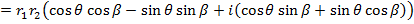
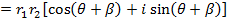
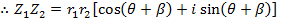
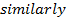
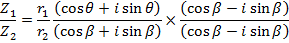
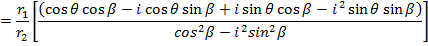
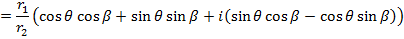
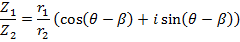
Example

If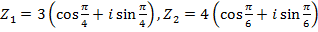  

Find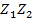 i)     ii)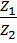

Solution

i)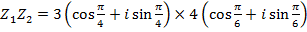

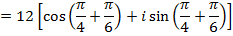
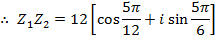
ii)