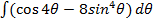ADVANCED MATHEMATICS FORM 6 – COMPLEX NUMBER

DEMOIVRE’S THEOREM

Demoivre’s theorem is a generalized formula to compute powers of a complex number in its polar form

Consider 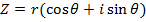 from the earlier discussion we can find (Z)(Z)

 

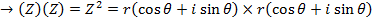
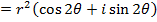
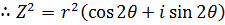
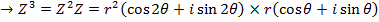
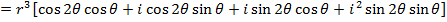
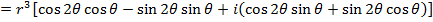
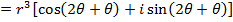
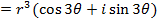
This brings us to Demoivres theorem

If 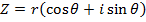 and n is a positive integer

Then

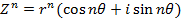
Proof demoivre’s theorem by induction.
Test formula to be true for n

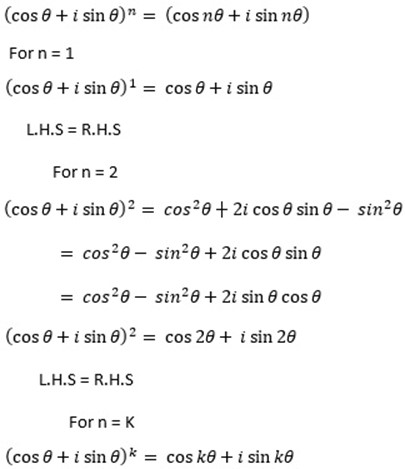
Let us show that the formula is true for n = k+1

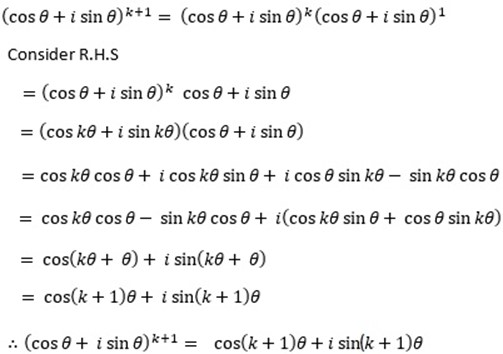
Since the formula was shown to be true for n = 1, 2 hence its true for integral value of n.

Example

1.   Find

Solution

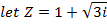
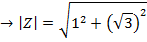
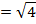
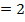
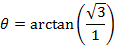
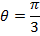
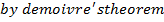
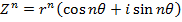
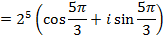
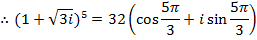
2.   From Demoivere’s theorem prove that the complex number 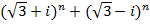  is always real and hence find the value of the expression when n = 6

Solution

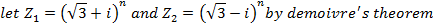
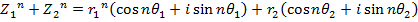
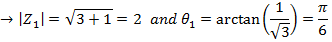
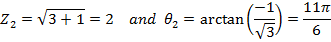
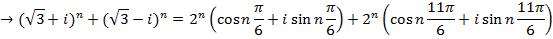
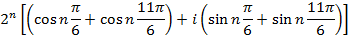
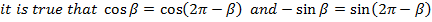
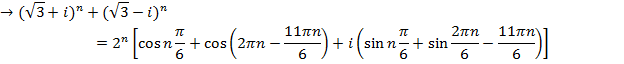
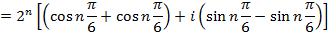
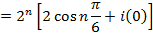
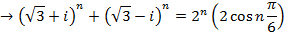
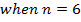
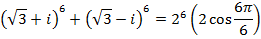
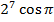
FINDING THE n^th ROOT

Demoivere’s formula is very useful in finding roots of complex numbers.

If n is any positive integer and Z is any complex number we define an n^th root of Z to be any complex number ‘w’ which satisfy the equation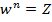

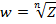
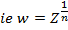
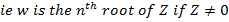
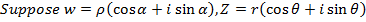
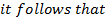
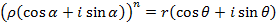
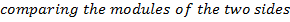
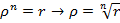
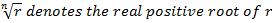
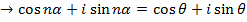
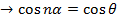
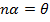
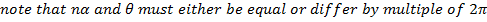
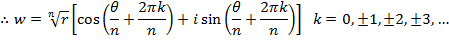
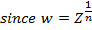
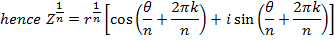
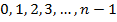
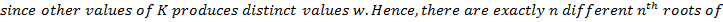
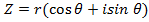
Examples

1.   Find all cube roots of -8

Solution

-8 lie on the negative real axis

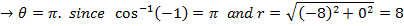
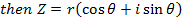
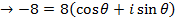
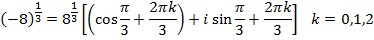
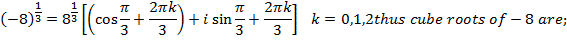
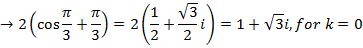
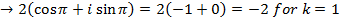
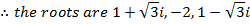
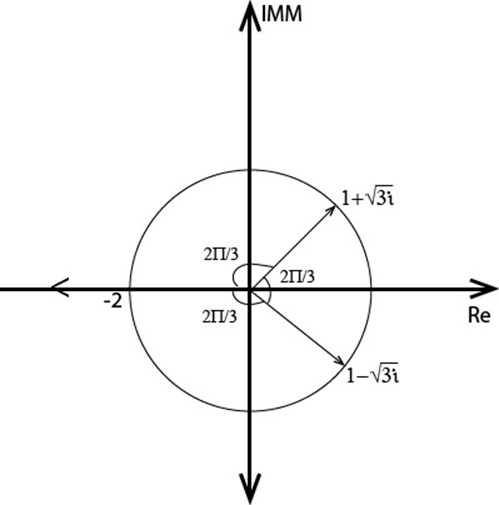
2.   Solve 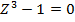 giving your solution in polar form

Solution:

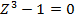
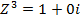
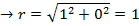
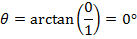
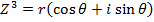
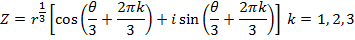
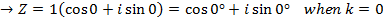
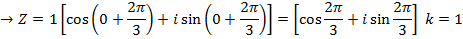
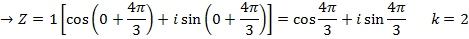
EXERCISE

1.   Find all fourth roots of 1.

2.   Evaluate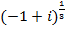

Proving trigonometric identities using Demoivre’s theorem

Examples

Prove that

i)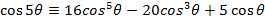

 ii)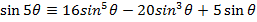

Solution

Note;

To solve such question you should be aware of the binomial theorem

i)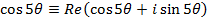

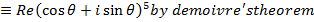
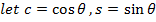
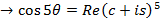
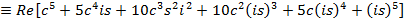
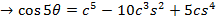
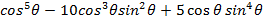
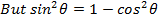
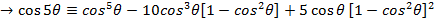
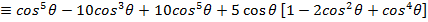
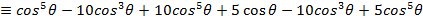
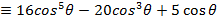
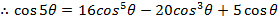
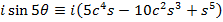
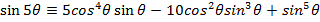
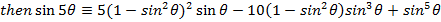
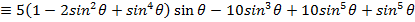
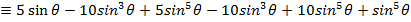
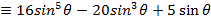
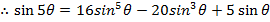
EXERCISE

Show that;

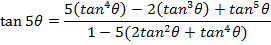
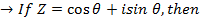
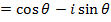
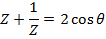
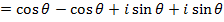
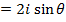
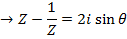
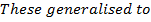
Example

Find an expression for

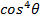i)               ii)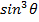

Solution

i) We know that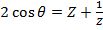

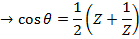
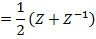
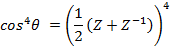
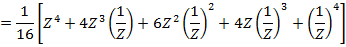
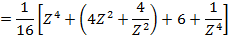
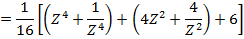
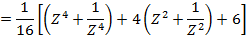
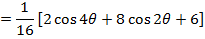
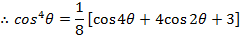
ii)

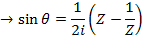
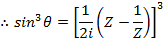
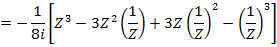
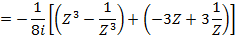
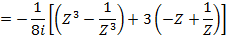
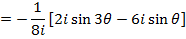
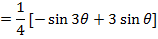
EXERCISE

Use Demoivre’s theorem to find the following integrals

a)

b)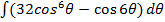

c)