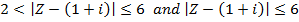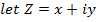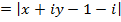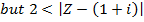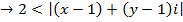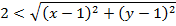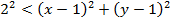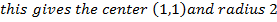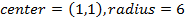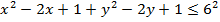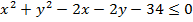ADVANCED MATHEMATICS FORM 6 – COMPLEX NUMBER

THE EULER’S FORMULA (THE EXPONENTIAL OF A COMPLEX NUMBER)

Euler’s formula shows a deep relationship between the trigonometric function and complex exponential

Since

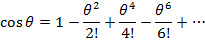
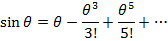
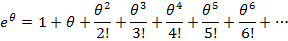
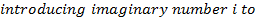
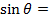
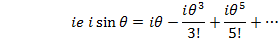
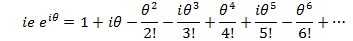
Re organizing into real and imaginary terms gives.

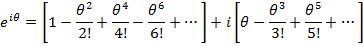
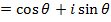
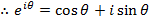
Hence if Z is a complex number its exponent form is 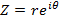 in which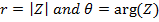  

Example

1. Write 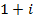 in polar form and then exponential form

Solution

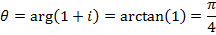
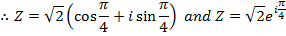
2. Express 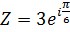 in Cartesian form correct to 2 decimal places

Solution

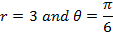
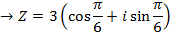
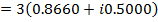
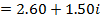
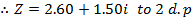
Note that;

The exponents follow the same laws as real exponents, so that

If

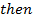
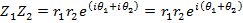
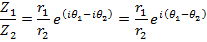
ROOTS

Sometimes you can prefer to find roots of a complex number by using exponential form.

From the general argument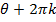

If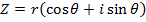

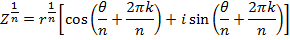
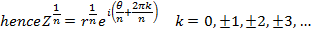
Example

Find the cube root of Z = 1

Solution

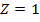
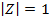
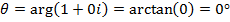
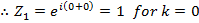
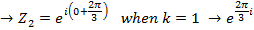
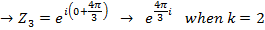
Example 2

Calculate the fifth root of 32 in exponential form

Solution

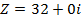
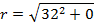
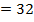
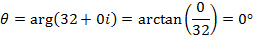
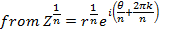
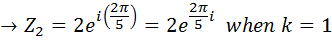
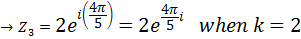
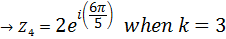
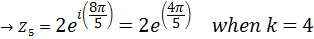
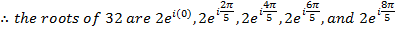
LOCI OF THE COMPLEX NUMBERS

Complex number can be used to describe lines and curves areas on an Argand diagram.

Example 01

Find the equation in terms of x and y of the locus represented by |z|=4

Solution

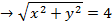
This is the equation of a circle with centre (0.0) radius 4

Example 02

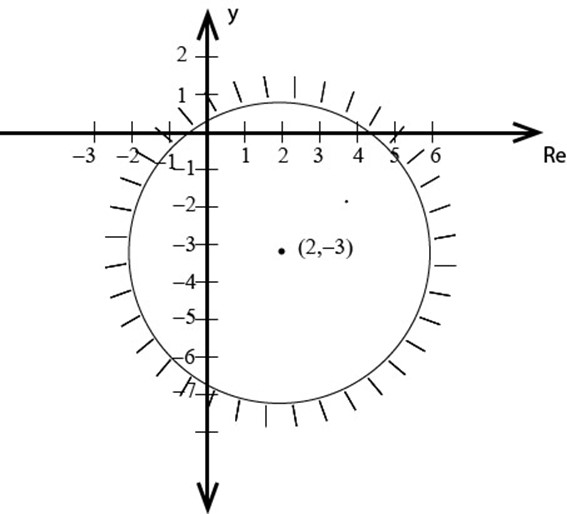
Describe the locus of a complex variable Z such that

Solution

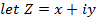
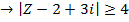
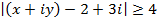
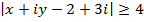
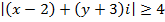
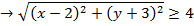
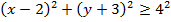
This is the equation of a circle with centre (2,-3), radius 4 in which the point  (x, y) lies on  and out of the circle.

Example 03

If Z is a complex number, find the locus in Cartesian coordinates represented by the equation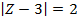

Solution

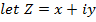
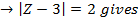
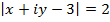
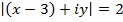
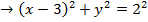
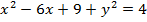
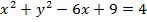
This is the needed locus which is a circle with centre (3, 0) and radius 2

Example 04

If Z is a complex number, find the locus of the following inequality

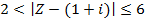
Solution

We consider in two parts