Introduction
The position of points on a line found by using a number line, that is
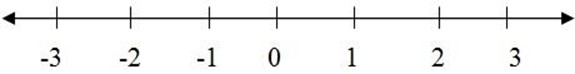
When two number lines one vertical and another one horizontal are considered one kept at 90o and intersecting at their zero marks, The result is called xy – plane or Cartesian plane. The horizontal one is called x – axis and the vertical is called y – axis.
Origin is the where the two axes that is x – axis and y axis (intersect)
Coordinates of a point
The position of a point in the xy – plane is given by a pair of in the form of ordered pair. Thus ordered pair is called coordinate. The coordinate of the point is therefore written in the form of (a, b), Where the first number ”a” is the value in the horizontal axis i.e x – axis b is the value in the y – axis
The value in the x – axis is also referred to as abscissa and y – axis is called ordinate. All distance in the xy – plane are measured the origin.
Examples write the coordinates of the following point A, B, C, D, E, F
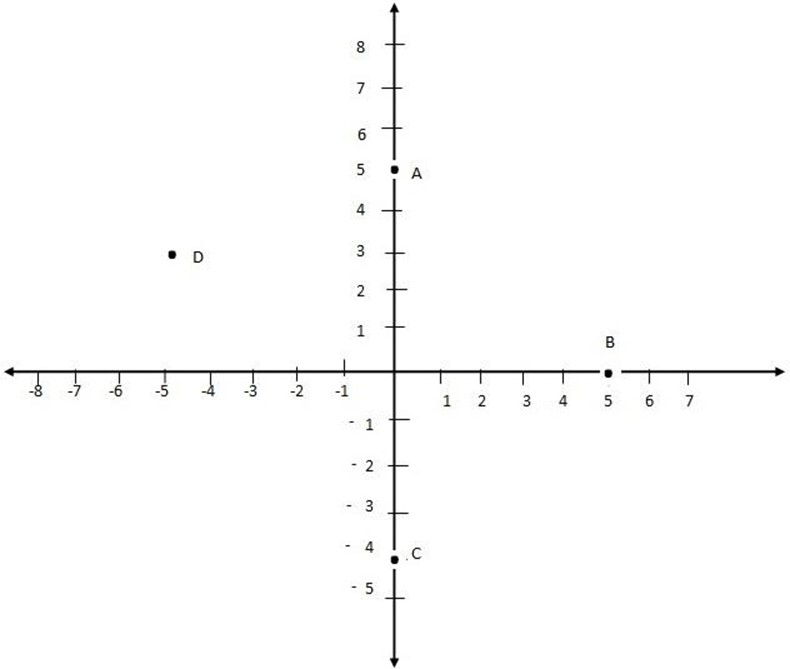
Solutions
The coordinates of the points are
A = (0,5)
B = (5,0)
C = (0,4)
D = (-5,5)
Exercise 10.1
1. a) Write down the coordinates of each of the labeled points in figure 9.2
b) State the quadrant in which each of these points F, H, V and I belong
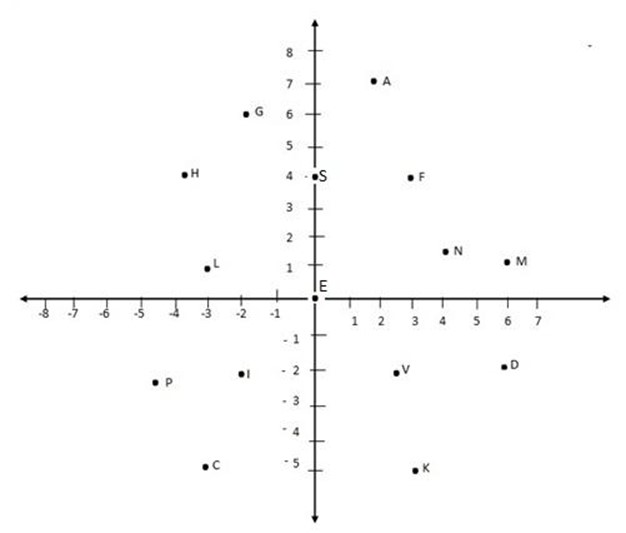
2. Draw axes on a graph paper and plot the points given below. Join in the order given with straight lines forming polygonal figures shape have you drawn in each case.
a) (1, 1), (3, 1), (3, 3), (1, 3)
b) (-2, 1), (2, 5), (2, -2)
c) (3, 1), (5.4, 1) (4.3, 2), (3.3, 2)
d) (5.5, 3.4), (6.5, 3.4), (6.8, 4.3), (6.0, 4.9), (5.2, 4.3)
e) (1.5, -3), (6, 3), (1.5, 3), (-6, -3)
f) (-1, 0), (-2, 2), (0, 1), (2, 2), (1, 0), (2, -2), (0, -1)
SLOP/GRADIENT OF A LINE
Slope / gradient is the change in the vertical axis to the change in the horizontal axis.
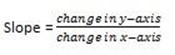
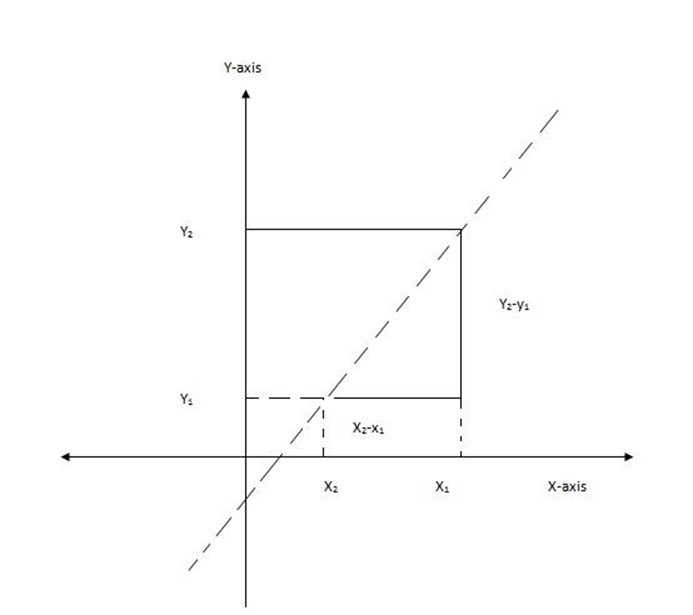
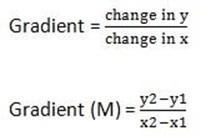
Example: Find the gradients of the lines joining
(a) A (2, 4) and B (-2, 6)
(b ) A (-2, -2) and B (2, -4)
(c) A (0, -1) and B (2, 3)
Solution
a. Let (x1, y1) be (2, 4) and
(x2, y2) be (-2, 6)
M=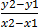
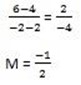
b. let (x1, y1) be (-2, -2)
(x2, y2) be (2, -4)
M =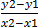
= 
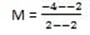
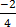
m=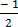 
c. A (0, -1) and B (2, 3)
Solution
Let (x1, y1) be (0, -1)
(x2, y2) be (2, 3)
M =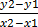
= 
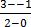M = 2
Exercise 10.2
1.Plot pair of the following points on a graph paper and join them by straight line. For each pair, calculate the gradient of the line and state whether it is positive, negative, zero or undefined.
(a) (0,3), (2,5)
(b) (5,8), (4,1)
(c) (1,5), (4,7)
(d) (2,6), (5,3)
(e) (1,6), (3,-1)
(f) (3,6), (-2,-1)
(g) (0,2), (6,2)
(h) (2,3), (-1,-3)
(i) (2,10), (2,0)
(j) (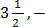
–
), 
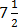, 2)
(k) (-2,1), (4,3)
(l) (-4,4),(-3,3)
(m) (0,0), (-3,4)
(n) (99,6), (119,1)
(o) (0.64,-1.62, (1.36,-0.62))
EQUATION OF A LINE
We have already discussed how to find the gradient of a line for example the gradient of the line joining points (2, – 4) and (5,0) is given as.
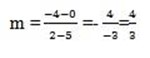
Since the two points are collinear.
we can find the equation of the line having any point on a line say (x,y) and any point,
then from
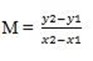
let (x1,y1) = (x,y), and (x2,y2) = (5,0)
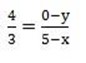
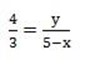
4(5-x) = 3x-y
20-4x = -3y
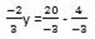
∴y =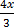 
– 
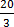
In general the equation of a straight line is written as y = mx + c. Where m – Is the slope of the line and c is ordinate of the y. called y- intercept
The point on the line (x,y) is called arbitrary point
Example: – find the equation of line passing through the points.
(12,-6) and (2, 6)
Solution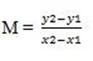
let (x,y)=(12,-6),
(x2-y2)= (2,6)
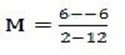
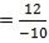
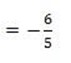
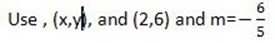
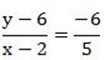
5(y-6)=-6(x-2)
5y-30=-6x+12
5y=-6+12+30
5y=-6x+42
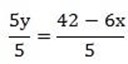
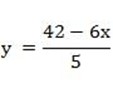
(2) Give that y = –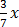 
+ 6 find the gradient of this line
The gradient is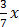 
Example: find the equation of the line passing through the point (4, 6) and having a slope -1/2
Solution
(x,y) , (4,6) , M = 
= 
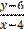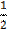
2(y-6) = x – 4
2y – 12 = x – 4
2y = x + 8
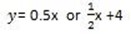
X-intercept and y – intercept.
X-intercept is the point where a line meets (cuts) the x-axis, at the value of y (ordinate) is equal to zero.
That is to say the x-intercept is found by substituting y = 0 in the equation. Therefore for the equation y = mx + c.
Y = 0, 0 = mx + c
Mx + c = 0
Mx = -c
x= -c/m.
Therefore the coordinate of x-intercept is (-c/m, 0).
y- Intercept is the point where the line and the y- axis meet. All this point the abscissa is normally equal to zero. The x- intercept is found by setting. x=0
i.e y = mx + c
x=0
y = m(0) + c
y = c
The intercept (0,c)
The coordinate of the Y-intercept is (0,c)
Example : – a line L is passing through the points A(5 – 2) and B(1,4).
Find
i. The equation of the line in the form of
Y= mx +c and ax + by + c = o
ii. The x and y intercept.
Solution:
i.
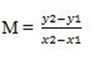
(x,y) = (1,4)
= 
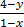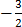
-3 + 3x = 8 – 2y
2y = 11- 3x
Y =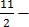
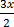
Y=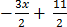
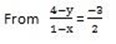
then -3 + 3x = 8 – 2y
-3 + 3x = 8 – 2y
-3 + 3x – 8 + 2y = 0
3x – 11 + 2y = 0
3x + 2y – 11 = 0
(ii) Y – intercept
Let x = 0
3x + 2y – 11 = 0
= 
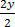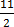
y =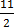 
Y – Intercept =0,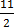 
The coordinate of Y-intercept is (0,11/2)
∴ find the x-intercept
Let y=0
mx + c = y
0 =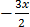 
+ 11
x =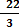
The coordinate of X-intercept is (22/3,0)
(iii) If ax + by = 12 goes through points (1,-2) and (4, 1) find the value a and b-
solution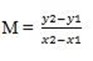
+
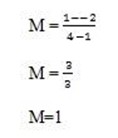
let the two collinear point be (x,y),(4,1) and gradient 1
then from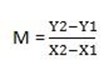 
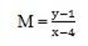
x-4 = y-1
x-y=–1+4
x-y=3
if the equation is multiple by 4 both side we have
4(x-y)=4×3
4x-4y=12
compare the equations.
x-y=3 and ax+by=12
ax+by=4(3)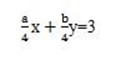
x-y=3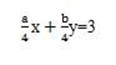
then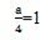
a=1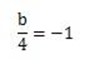
b=-4
The value of a=1 and b=-4
EXERCISE 10.3
3. Find the equations of lines through points
a) (2,1) with gradient 2.
b) (0,5) with gradient -2
c) (1,-3) with gradient-3
d) (-2, -4) with gradient 
e) (0, 0 ) with gradient -3
f) (-3 , -3) and y- intercept 
g) ( 6, 2) and y intercept -2
h) (-1 , -1 ) and y – intercept – 
i) ( 1 , 2 ) and y- intercept = 2
j) (5 , 5) and y intercept 0
2. Find the equations of the following lines
a. (i) y – intercept – 2 , gradient 1
b. (ii) y – intercept 7, gradient 
(iii) y- intercept -16, gradient 4
d. (iv) y -intercept 2, gradient – 10
e. (v) y- intercept 0.4, gradient -0.7
(3) Rewrite the following equations in the form y = mx + c, and then determine the gradient and the y- intercept of each.
a) (i) 7x + 4y = 11
(ii) 14x + 3y = 12
c) (iii) 2x = 5 + y
d) (iv) 4x + 5y = 40
(v) 8x – (
)y = 0
(vi) 6x = 5 – 2y
(vii)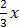 
+ 
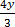= 9
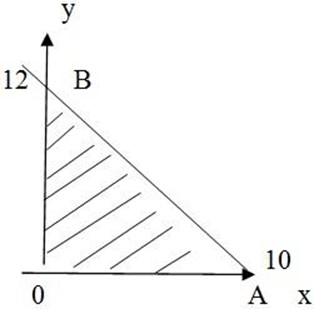
Qn. 4. Find the area of the shaded region in the following figure. If the equation line AB is 5x + 6y-60 =0
SIMULTANEOUS EQUATIONS
Are equations of more than one variable which can be solved at the same time. There are two ways of solving simultaneous equations.
1. (i) Elimination method
(ii) Substitution method.
(iii) Graphical Method
The principle of solving equations is that the number of equations should be equal to the number of unknowns
Example of simultaneous equation
(a) =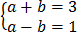 
(b) =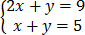 
These are examples of simultaneous equations with two unknowns.
1. Elimination method
Is the method of omitting one variable and solve the remaining variables.
How to eliminate
i. Check if there are equal coefficients
ii. If there are equal coefficients of same variables in the both equations subtract.
iii. If there are equal and opposite to coefficients of same variable in both equations, add.
2. If all coefficients are different modify the equations
Example 1. 2x + 3y = 6
3x + 2y = 4
Modification
Omitting: x
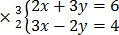
here we can now omit x by subtracting.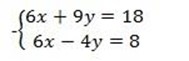
13y=10
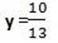
Omitting y
+ 
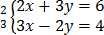
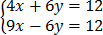
13x=24
=
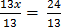
x=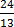
Let find the value of y by take one equation
2x+ 3y=6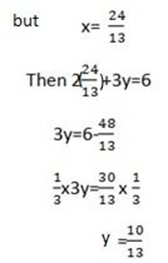
Example 2:
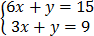
Solution
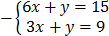
3x=6
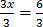
x =2
Let find the value of y by take one equation
6x+y=15
6 
2 + y = 15
12 + y = 15
y = 15 – 12
y = 3
∴x =2 and y = 3
Example 03:
2x + y = 10
3x – 2y = 1
Solution. by Eliminate
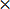
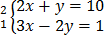
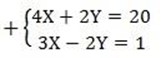
7x= 21
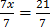
x=3
Let find the value of y by taken one equation
3x-2y=1
3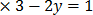
9-2y=1
-2y=1-9
= 
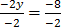
y= 4
y=4 and x = 3
Solve the following simultaneous equations by elimination method
1. x + y = 7
5x + 12y = 7
Solution
Modify
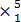
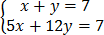
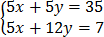
-7y = -28
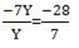
y= 4
Let find the value of x by taken one equation
x + y=7
x + 4 =7
x=7- 4
x=3
Therefore: x=3 and y = 4
2. x + 8y =19
2x + 11y = 28
Solution
=
= 
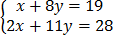
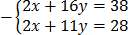
5y=10
= 
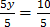
y= 2
Let find the value of x by take one equation
x + 8y = 19
x + 8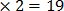 
x=19-16
x = 3
Therefore: x=3 and y = 2
3. 8x + 5y = 9
3x + 2y = 4
Solution
– 
= 
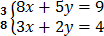
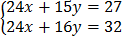
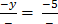
y=5
Let find the value of x by taken one equation
8x + 5y = 9
8x + 5(5) =9
8x + 25 = 9
8x = 9 – 25
8x = -16
= 
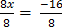
x = -2
Therefore: x = -2 and y = 5
4. 2x- 3y = 7
15x + y = 9
Solution
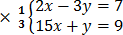
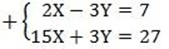
17x = 34
= 
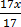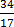
x = 2
Let find the value of y by taken one equation
2y – 3y = 7
2(2) – 3y =7
-3y=7-4, -3y=3
4 – 3y = 7
= 
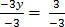
y=-1
Therefore: x = 2, y = -1
5. 2x + 3y = 8
2x = 2 + 3y
solution
2x + 3y = 8
2x -3y = 2
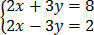
6y=6
= 
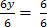
y=1
Let find the value of x by taken one equation
2x + 3y = 8
2x + 3(1) = 8
2x = 8-3
x=5
=
= 
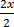x = 
Therefore: x= 
and y = 1
6. 3x – 4y = 20
x + 2y = 5
Solution
– 
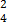
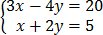
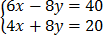
2x = 20
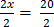
x= 10
Let find the value of y by taken the one equation
x + 2y =5
10+ 2y = 5
2y = 5 – 10
= 
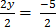
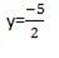
Therefore: y =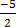 
and x = 10
7. 6x = 7y + 7
7y – x = 8
Solution
= – 
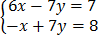
5x= 15
= 
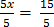
x=3
Let find the value of y by taken one equation
6x – 7y =7
6 (3) -7y = 7
Therefore :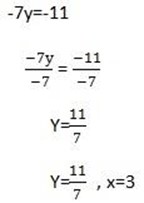 
8. y = 4x – 7
16x – 5y = 25
solution
-4x + y = -7
16x – 5y = 25
+ 
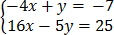
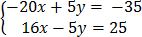
-4x=-10
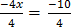
x = 2.5 or 5/2
Let find the value of y by taken equation one
y – 4x = -7
y = – 4 (2.5)= -7
y = -7 +10
y= 3
Therefore x = 2.5 and y = 3
9. 2x + 7y = 39
3x + 5y = 31
solution
– 
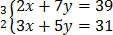
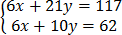
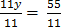
y= 5
Let find the value of x by taken one equation
3x +5y = 31
3x+ 5(5) = 31
3x=31- 25
= 
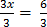
x = 2
Therefore: x = 2 and y = 5
10. 15x – 8y = 29
17x + 12y = 75
Solution
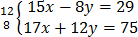
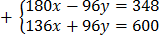
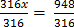
x =3
Let find the value of y by taken one equation
15x – 8y = 29
15(3) – 8y = 29
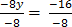
Therefore: y = 2 and x = 3
2: SUBSTITUTION
Example: 01 solve
6x + y = 15
3x + y = 9 by substitution method.
solution
6x + y = 15 ……… (i)
3x + y = 9……….. (ii)
from equation 1
6x+y =15
y=15-6x……………..(iii)
Substitute equation (iii) into (ii)
3x + y = 9
3x + 15 – 6x = 9
3x – 6x + 15 = 9
-3x = 9 – 15
-3x=-6
= 
= 
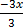x=2
y = 15 – 6x
y = 15 – 6 x 2
y= 15 – 12 = 3
x= 2 and y = 3
Example 02
2x + y = 10……………..(i)
3x – 2y = 1………………(ii)
From (i)
2x + y = 10
2x – 2x + y = 10 – 2x
y = 10 – 2x ……………..(iii)
Put (iii)into (ii)
3x – 2 (10 – 2x) = 1
3x – 20 + 4x = 1
3x + 4x – 20 = 1
= 
= 
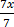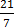
∴x = 3
y = 10 – 2x
y = 10 – 2 (3)
y = 10 – 6
y = 4
∴x = 3 and y = 4
Solve:
3x + 2y = 8………. (i)
2x + 3y = 12…… (ii)
solution
from (i)
3x + 2y = 8
2y=8-3x
= 
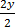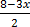
Y =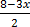 
……. (iii)
Put (iii) into (ii)
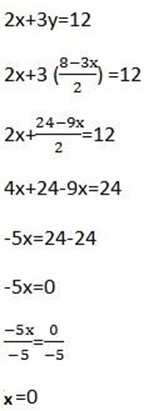
3x + 2y = 8
3(0) + 2y = 8
2y=8
= 
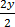∴Y = 4
X = 0 and y = 4
Exercise 10 .4
1. Solve the simultaneous equations by using elimination method.
(i). 2x + y = 5
4x – y = 7
(ii) 3x + y = 6
5x + y = 8
(iii) 5x – 2y = 16
x + 2y = 8
(iv) 8x+5y=40
9x + 5y = 5
(v) 7x – 4y = 17
5x – 4y = 11
(vi) 0.7x – 0.5y = 2.5
0.7x – 0.3y = 2.9
2. Solve the following simultaneous equations by using substitution method
(i). 3x – 2y =
2x + y = 8
(ii) 5x + y = 23
3x- 2y = 6
(iii) x – 3y = 2
4x + 2y = 36
(iv) 7x – y = 14
8x – 2y = 16
(v) 7x + y = 14
8x – 2y = 16
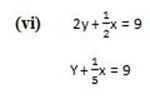
3. Solve the following by using any method
(i) 3y – x =
y + 2x = 6
(ii) 8m – n = 38
m – 3n = -1
(iii) 5x – 2y = 10
-x + 3y = 24
1. 4.Solve the following simultaneous equations by substitution method
(i) x – y = -3
2x – y = -5
(ii) X – 2y = 6
X + 2y = 2
3. (iii) 3x – 4y = -11
2x + 3y = 1
4. (iv) 2x – 3y =32
3x – 4y = 30
(v) 5a – 5b = 7
2a – 4b = 2
5. Solve the following system of simultaneous equations by elimination.
6. (i) 10u + 3v – 4 = 0
6u + 2v – 2 =0
(ii) x – y = 1
4x + 3y = 
(iii) 3x + 3y = 15
2x + 5y =14
(iv) 7x – 3y = 15
5x- 2y = 19
(v) x + y = 5
x – y = 1
6. Solve the following by any method
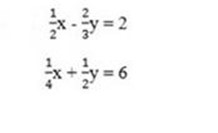
Solving word problems leading to simultaneous equations.
1. A fathers age is four times the age of his son. If the sum of their ages is 60 years. Find the age of the son and that of the father.
Solution.
Let x be the age of the son
Let y be the age of father
y = 4x……………….. (i)
x+ y = 60 …………(ii)
By substitution method
x + y = 6, but y=4x
then
x + 4x = 60
5x=60
= 
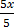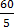
x = 12
By solve value of y you can take one equation
y= 4x
y = 4 (12) = 48
The age of the father is 48 years and that of the son is 12 years
2. 2. The sum of two number is 12 and their difference is 2 find the number
Solution
Let the first number be = x
Let the second number be= y
=
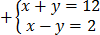
2x + 0 = 14
2x=14
= 
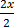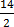
x = 7
Let find the value of y
7 + y = 12
y = 12 – 7
y = 5
The numbers are 5 and 7
Example 03. If the numerator of a fraction is decreased by 1 its value become2/3 but if it denominator is increased by 5 its value becomes ½ , what the fraction?
solution
let the fraction be a/b
= 
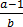…………….(i)
+ 5 = 
…………..(ii)
from (i)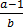 
= 
3(a-1) =2b
3a – 3 =2b
3a – 2b=3………………(iii)
from (ii)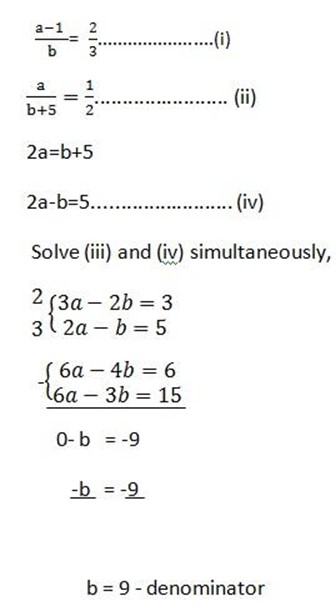
Example 4
The sum of the digits of a two digit number is 7. If the digits are reversed, the new number is increased by 3. Equal to 4 times the original number
Find the original number
Let the number be x and y
x + y = 7……………… (i)
The meaning of x, y = 10x + y
Similarly y, x = 10y + x
y, x + 3 = 4 (x, y)
10y+x+3=4(10x+y)
10y + x + 3 = 40x + 4y
6y+3=39x
= 
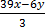13 x – 2y = 1……. (2)
= 
= + 
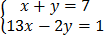
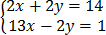
15x + 0 = 15
15x = 15
= 
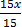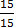
x = 1
Let find the value of y
x + y = 7
1+ y = 7 the number was x ,y is 1,6
y = 6
The original number is 16
Exercise 10.5
1. The sum of two number is 109 and the difference of the same numbers 29. find the numbers
2. Two number are such that the first number plus three times the second number is 1. And the first minus three times the second is 1/7. Find the two numbers
3. The sum of the number of boys and girls in a class is 36. If twice the number of girls exceeds the number of boys by 12, find the number of girls and that of boys in the class.
4. Twice the length of a rectangle exceeds three times the width of the rectangle by one centimeter and if one – third of the difference of the length and the width is one centimeter find the dimensions of the rectangle.
5. The cost of 4 pencils and five pens together is 6000 shillings while the cost of 6 pencils and 8 pens is 940 shillings, calculate the cost of one pencil and one pe
6. Half of Paul’s money plus one – fifth of John’s money is 1400 shilling John’s money is 2650 shillings. How much has each?
7. A farmer buys 3 sheep and 4 goats for shs 290,Another buys sheep and goats from the some market for shs 170.What price did they pay for (a) 1 goat (b) 1 sheep
SOLUTIONS.
EXERCISE 10.1
1. (a) Their coordinates are
A (2, 7)
J (0, 4)
F (3, 4)
N (4, 1.5)
M (6, 1)
V (2.5, -2)
D (6, -2)
K (3, -5)
C (-3, -5)
I (-2, -2)
P (-4.5, -2.5)
H (-4, 4)
G (-2, 6)
L (-3, 1)
E (0, 0)
(b) F belongs to quadrant I
H belongs to quadrant II
V belongs to quadrant IV
I belong to quadrant III
2 (a) Square
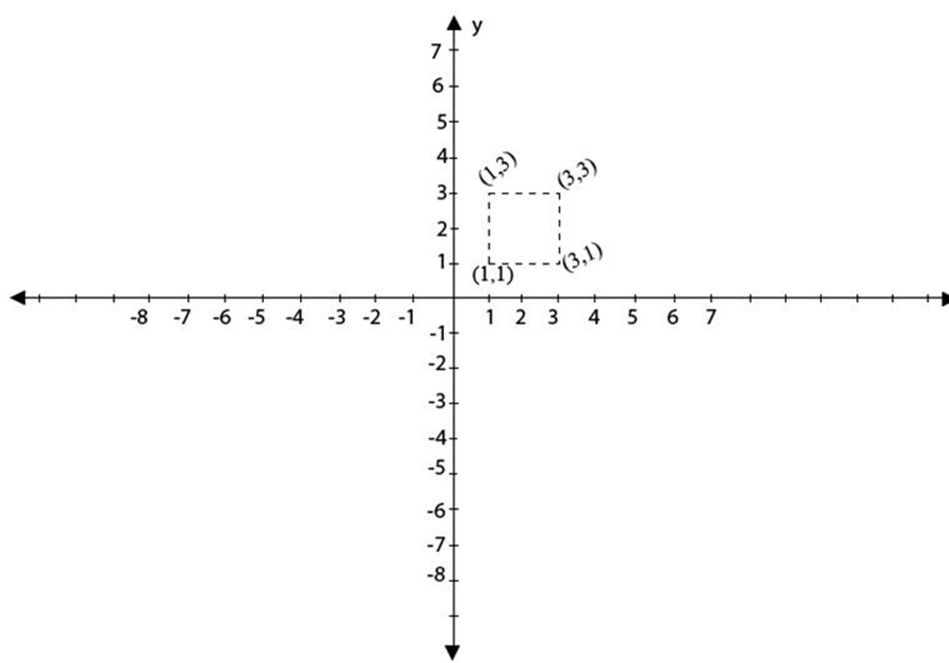
(b) Triangle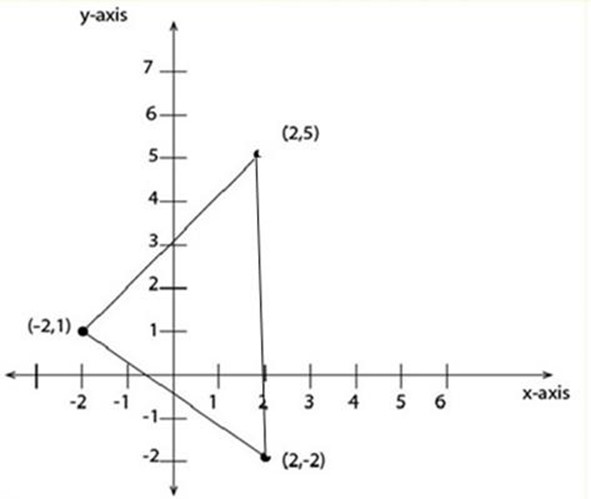 
(c) Trapezium
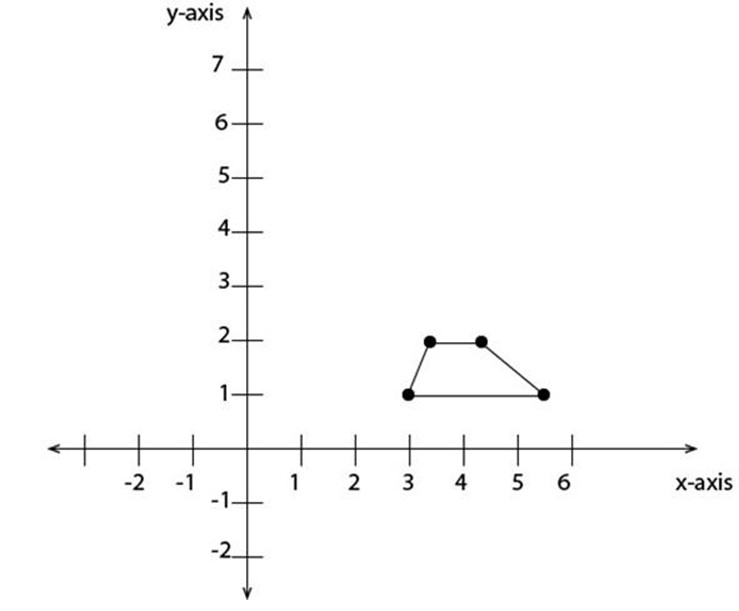
(d) Parallelogram
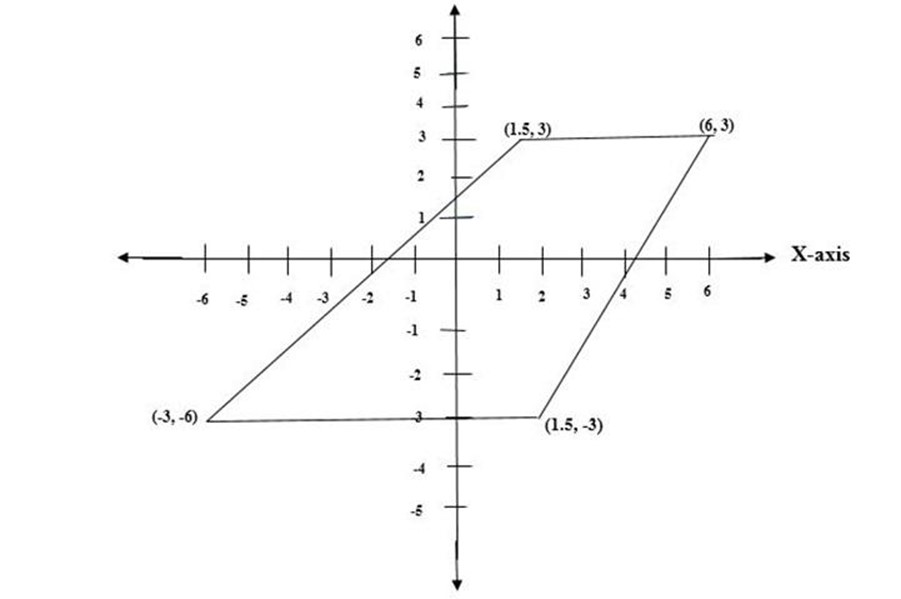
(e) Octagon
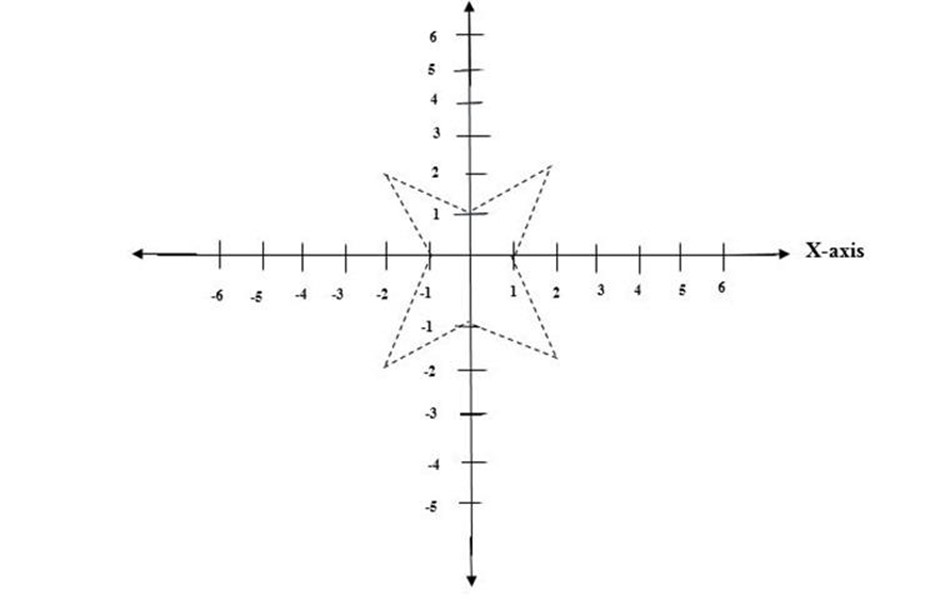
EXERCISE 10.2
1. a) (0, 3), (2, 5)
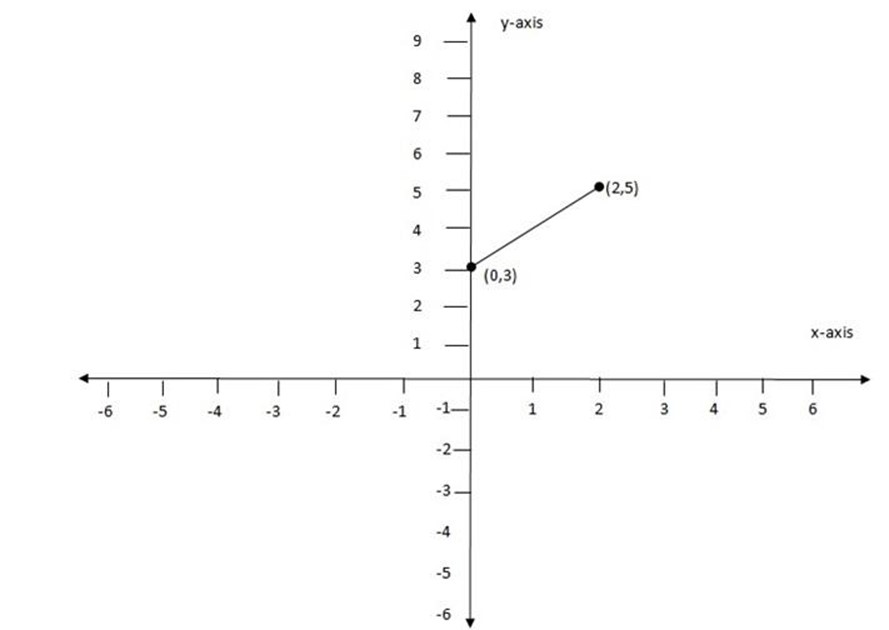
let (x1,y1) be (0,3)
(x2,y2) be (2,5)
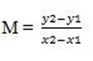
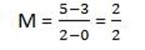
M = 1 it is positive gradient.
(b) (5, 8), (4, 1)
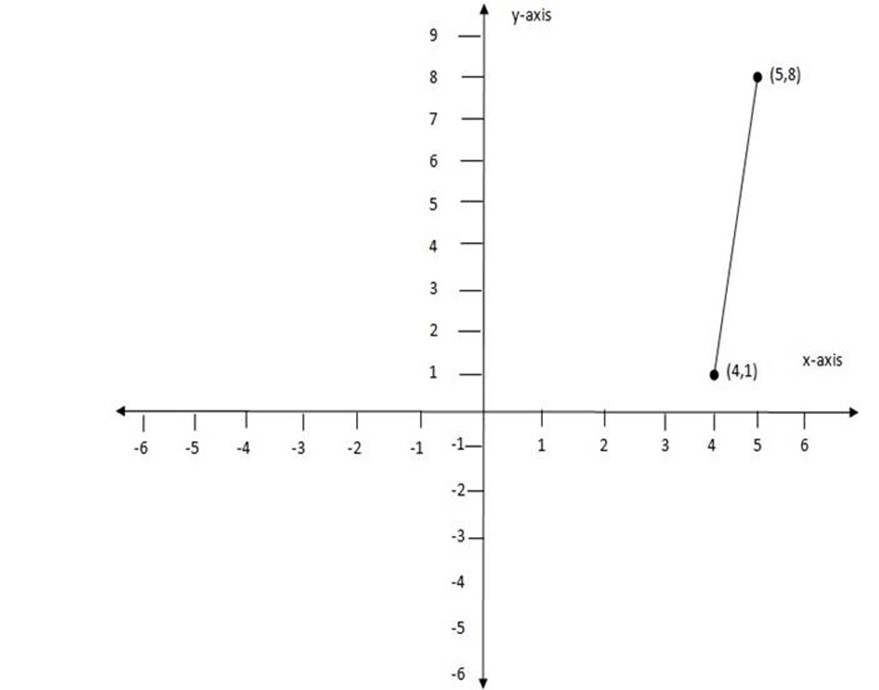
Let (x1, y1) be (5, 8)
(x2, y2) be (4, 1)
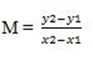
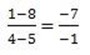
m= 7 Slope is positive
(c) (1, 5), (4, 7)
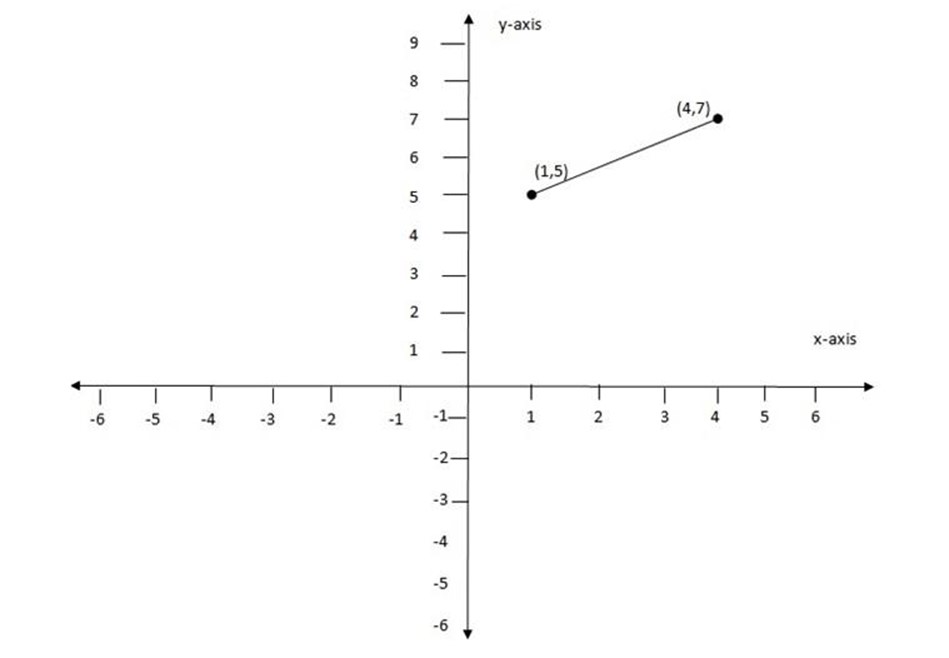
Let (x1, y1) be (1, 5)
(x2, y2) be (4, 7)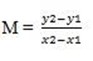
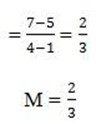
The gradient is positive
(d) (2,6), (5,3)
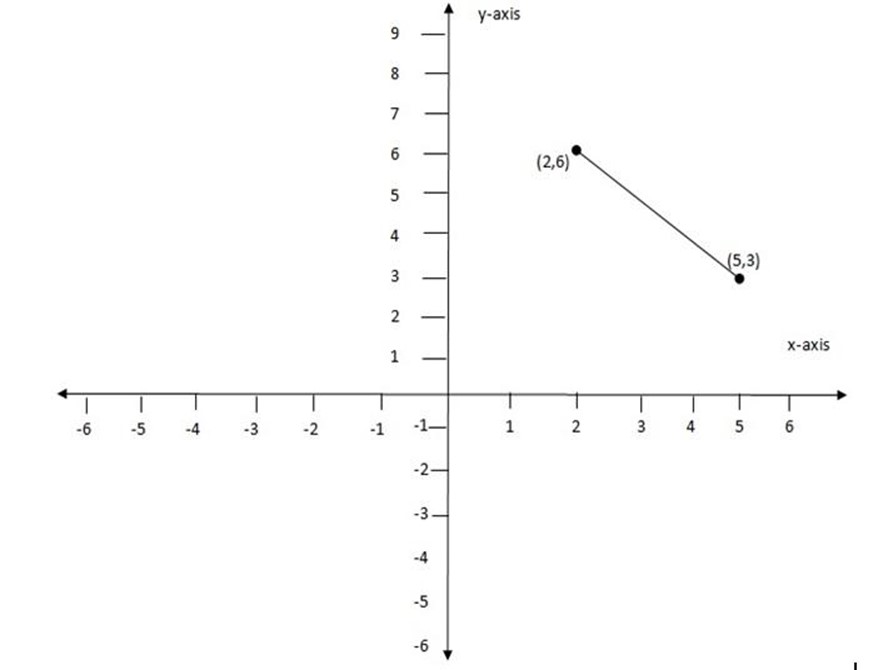
Let (x1, y1) = (2,6)
(x2, y2) = (5, 3)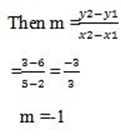
It has a negative gradient
(e) (1,6), (3, -1)
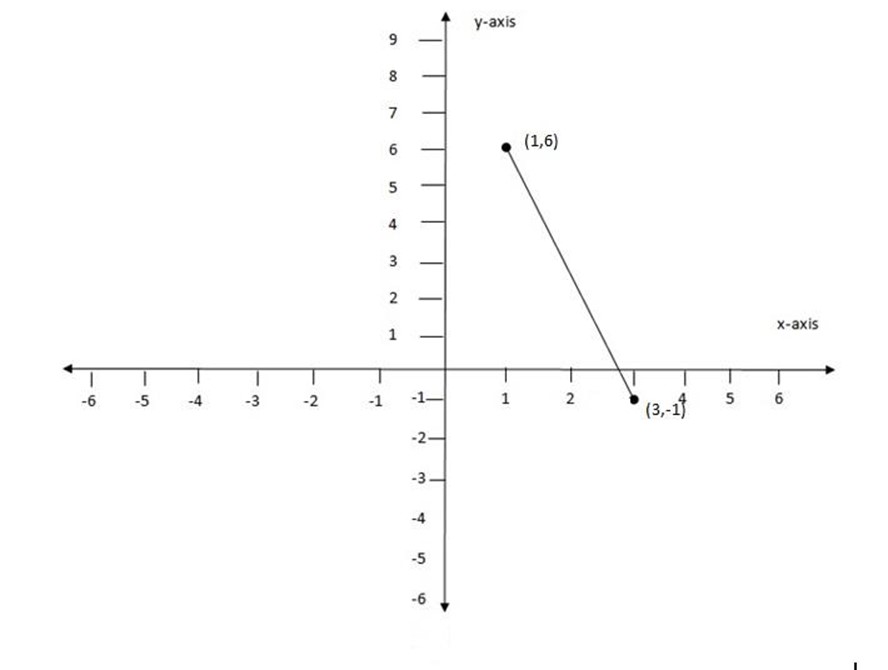
Let (x1, y1) be (1, 6)
(x2, y2) be (3, -1)
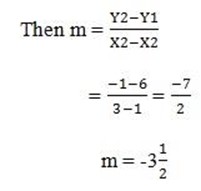The gradient is negative
(f) (3, 6), (-2, -1)
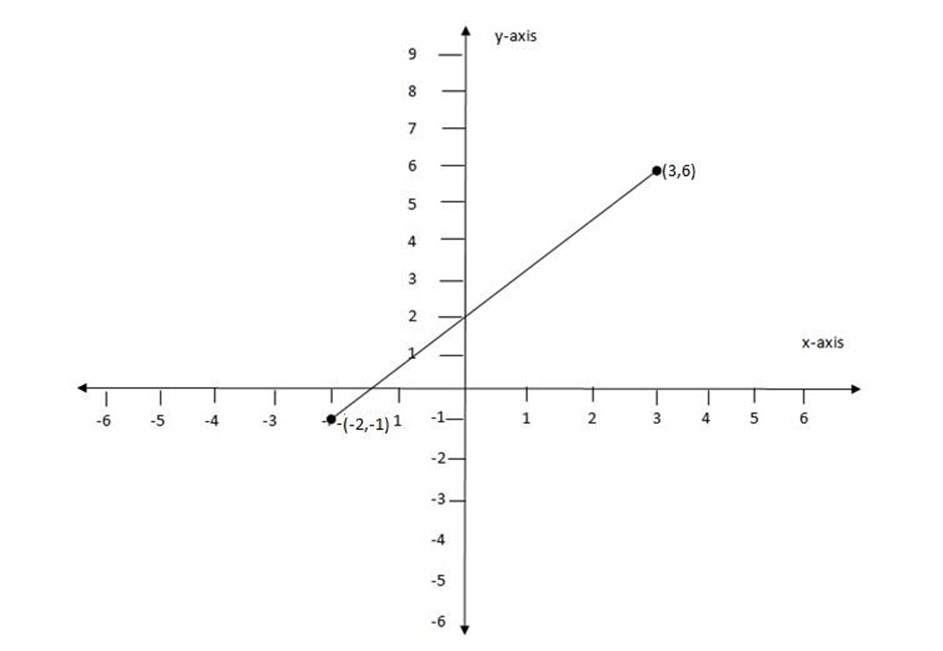
Let (x1, y1) be (3, 6)
(x2, y2) be (-2, -1)
m =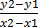
=
= 
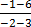
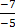
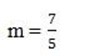The gradient is positive
(g) (0,2), (6,2)
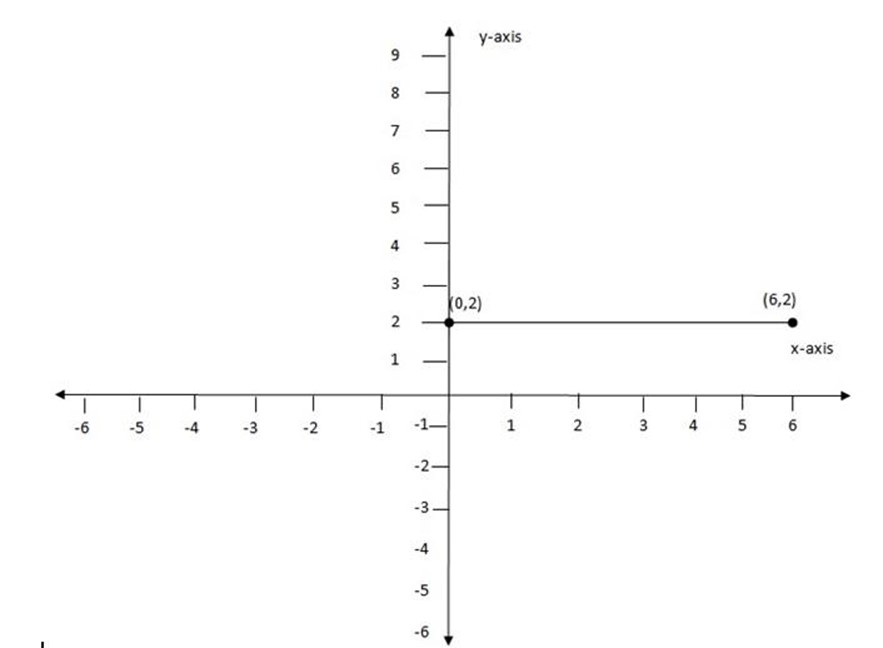
Let (x1, y1) be (0, 2)
(x2, y2) be (6, 2)
M =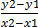
=
=
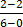= 0
M =0 The gradient is zero
(h) (2,3), (-1,-3)
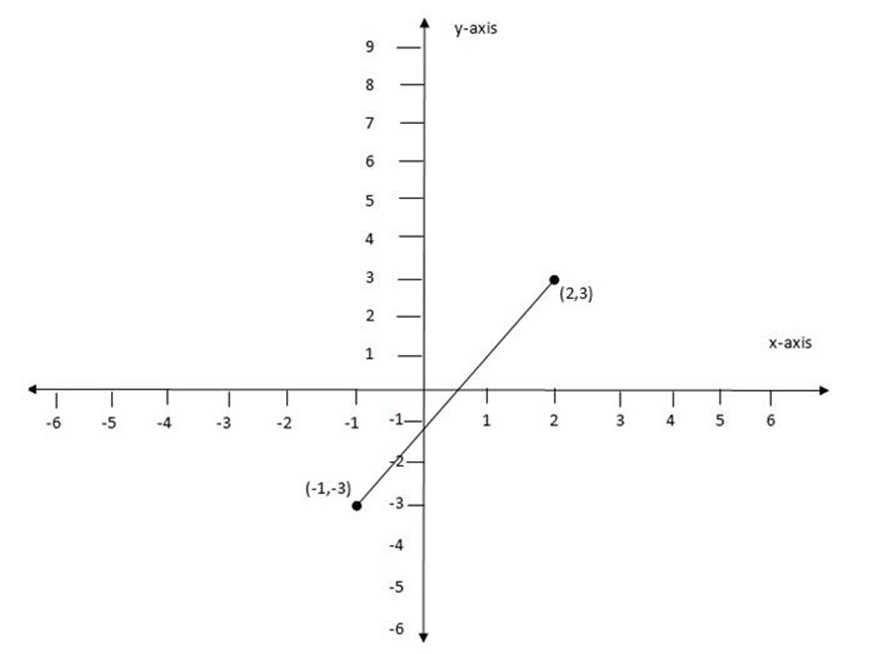
Let (x1, y1) be (2, 3)
(x2, y2) be (-1, -3)
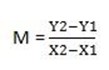
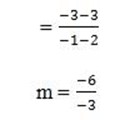
m = 2
The gradient is positive
(i) (2,10), (2,0)
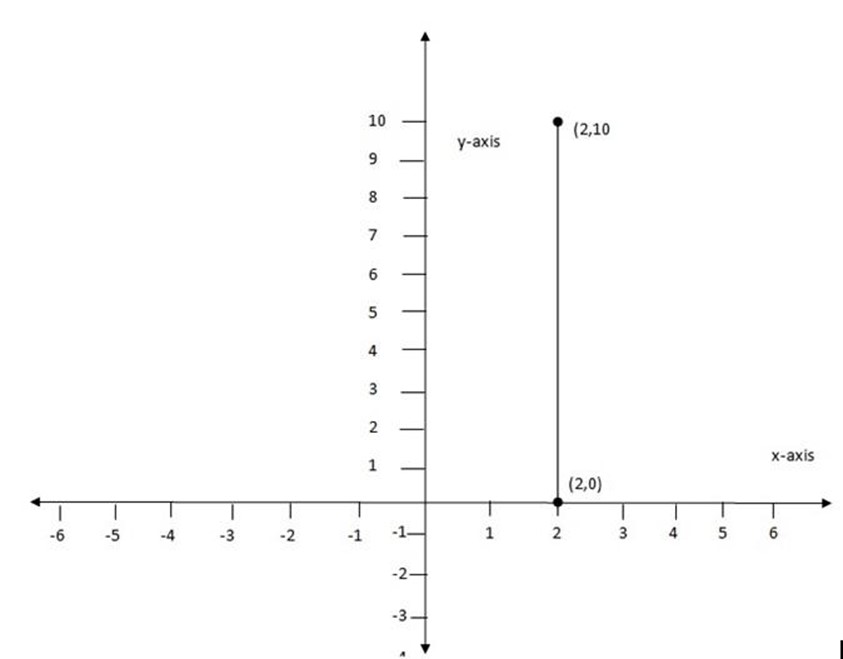
Let (x1, y1) be (2, 10)
(x2, y2) be (2, 0)
M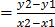
= 
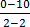
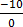
M is undefined
The gradient is undefined
(j) (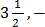
–
), 
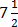, 2)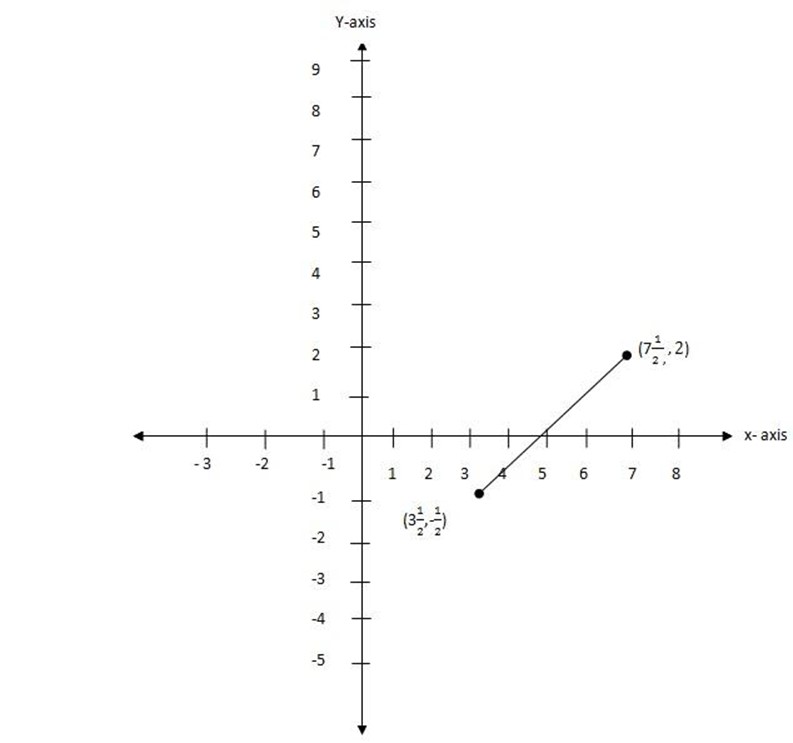
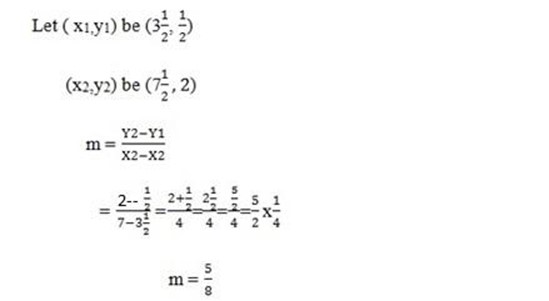
The gradient is positive
(k) (-2,1), (4,3)
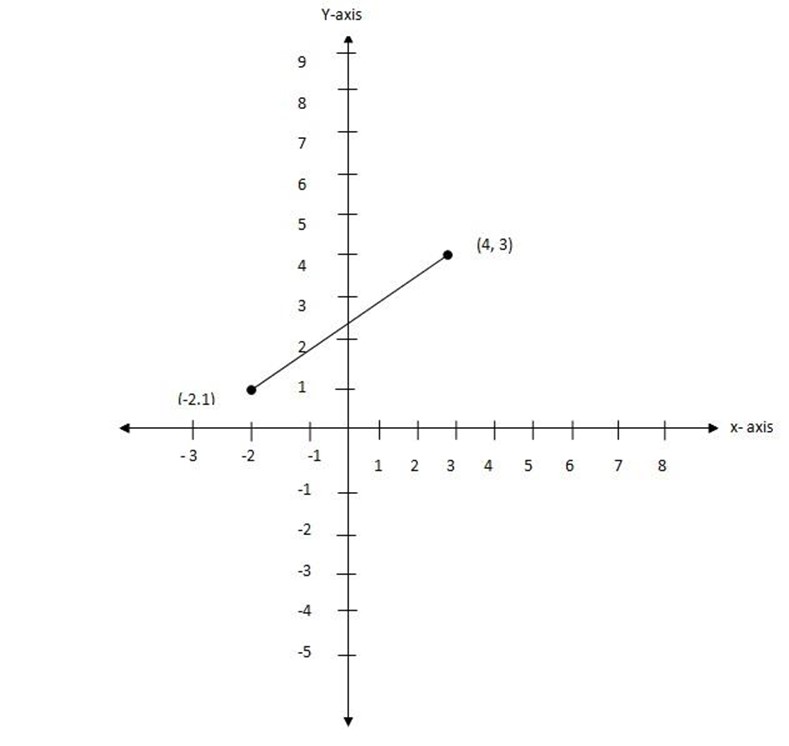
let (x1,y1) be (-2,1)
(x2,y2) be (4,3)
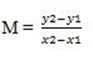
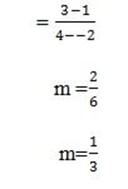The gradient is positive
(i ) (-4,4), (-3,-3)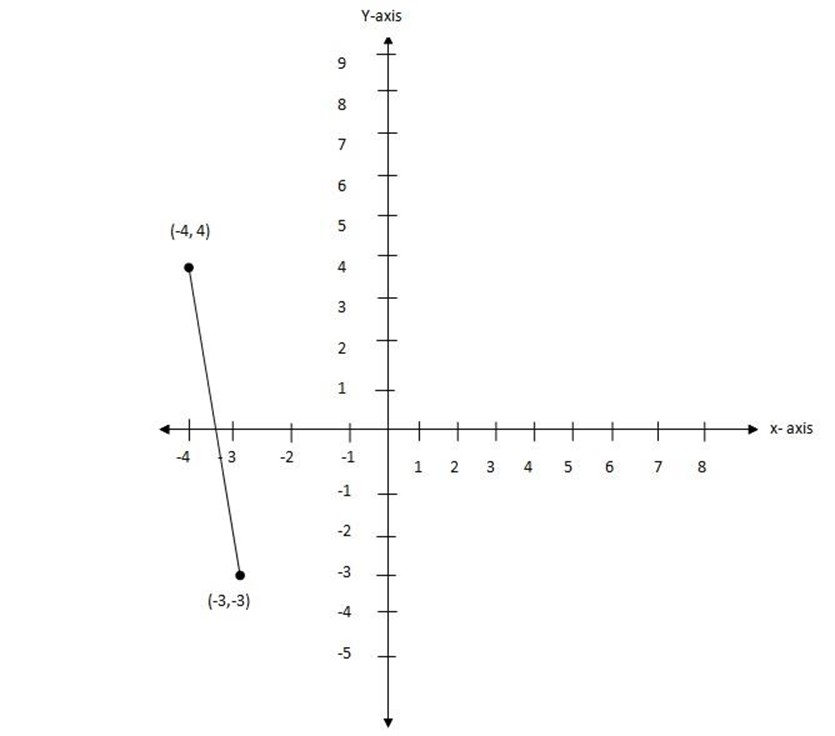
let (x1,y1) be (-4,-4)
(x2,y2) be (-3,-3)
M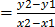
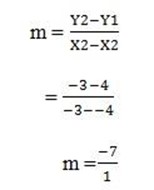
m= -7
The gradient is negative
(m) (0,0), (-3,4)
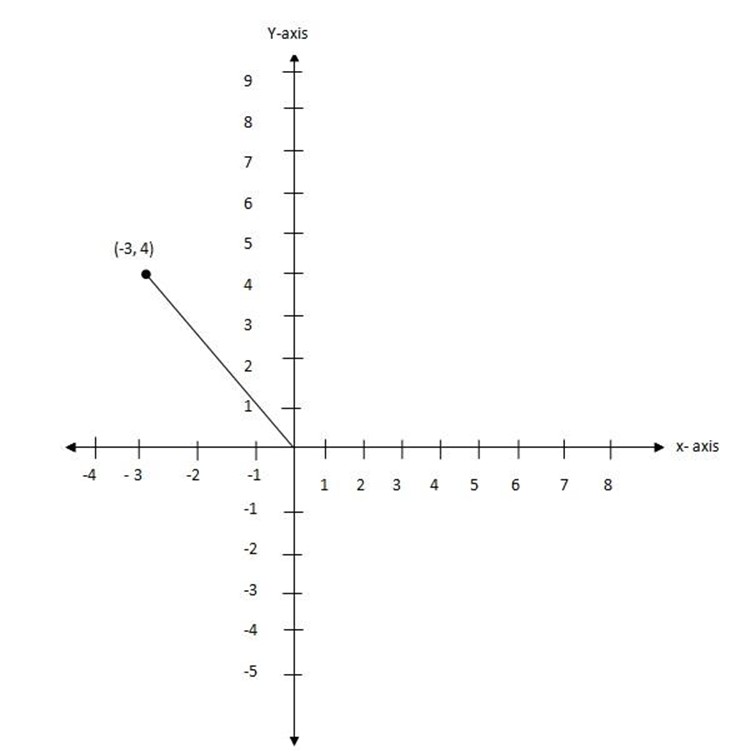
let (x1,y1) be (0,0)
(x2,y2) be (-3,4)
M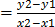
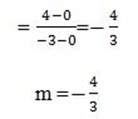
The gradient is negative
(n) (99,6), (119,1)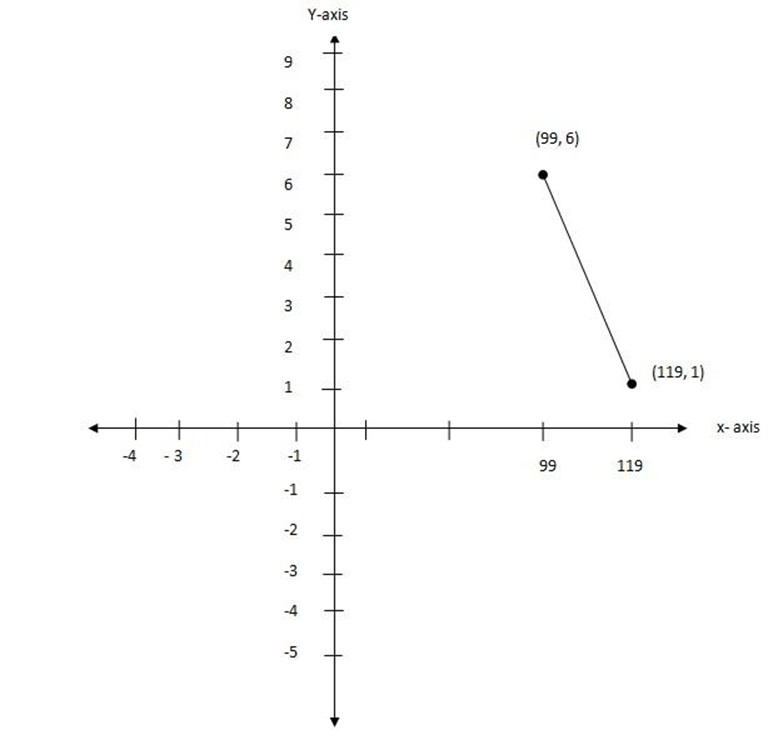
let (x1,y1) be (99,0)
(x2,y2) be (119,1)
M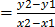
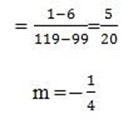
The gradient is negative
(o) (0.64,-1.62), (1.36,-0.62)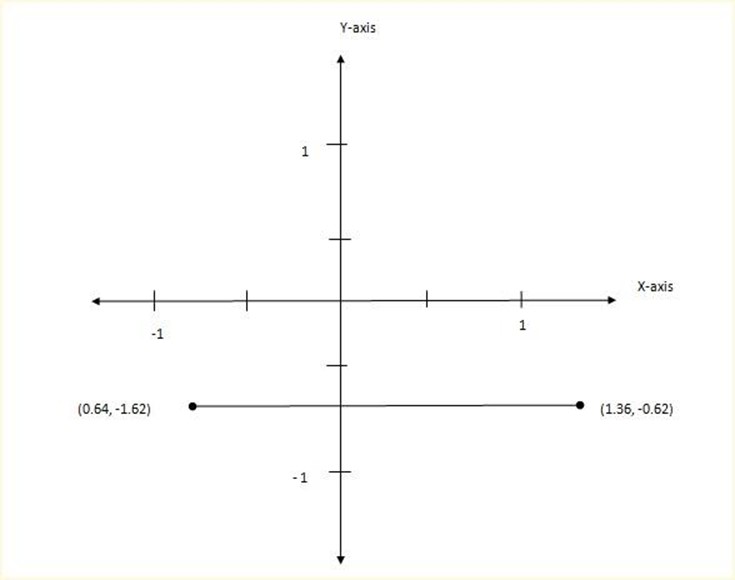
let (x1,y1) be (0.64,-1.62)
(x2,y2) be (1.36,-0.62)
M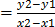
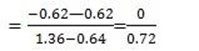
m=0
The gradient is zero
EXERCISE 10.3
1. a) (2,1) with gradient 2.
(x, y), (2, 1) m= 2
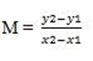
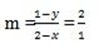
2(2-x) = 1(1-y)
4-2x = 1-y
4 -2x =1-y
y=1-4+2x
y= -3+2x
∴y = 2x – 3.
b) (0,5) with gradient -2
(x, y), ( 0, 5) m = -2
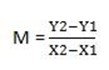
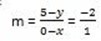
-2(0 – x) = 1(5-y)
0+2x = 5 –y
y= 5 -2x
∴ y= -2x + 5
c) (1,-3) with gradient -3
(x, y) , (1, -3) m = – 3
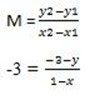
-3 – y = 3 – 3x
-y = – 3 + 3x + 3
-y = 3x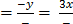 
y= -3x
d) (-2, -4) with gradient 3/2
(x, y) (-2 , -4) m = 3/2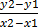
= 
= 
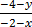3(-2 – x) = 2(-4 – y)
-6 – 3x = -8 – 2y
2y = 6 + 3x – 8
= 
+ 
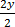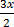
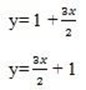
e) (0, 0 ) with gradient -3
(x,y) (0,0) m = -3
= 
= 
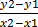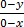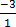
-3(0 – x) = 1(0 – y)
0 +3x = 0 – y
y = 0 – 3x
y = -3x
f) (-3 , -3) and y- intercept 1/2
Solution
(-3, -3)(x, y) y – intercept =1/2
Y = mx + c
(-3, -3),(x, y)
substitute (-3,-3) to y = mx +c
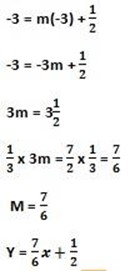
g) ( 6, 2) and y intercept -2
(6, 2), (0, -2)
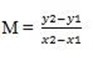
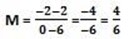
Gradient = 2/3
Arbitrary
(x,y), (6,2)
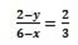
3(2-y) = (6-x)
6-3y = 12 – 2x
-3y = 12 – 6-2x
-3y = 6- 2x
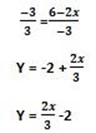
h) (-1 , -1 ) and y – intercept – 1/3
(-1, -1) and (0, -1/3)
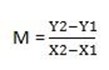
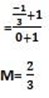
Arbitrary point = (x,y)
(x,y), (-1,-1)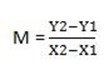
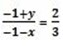
2(-1-x) = 3(-1-y)
-2-2x=-3-3y
3y=-3+2+2x
3y=-1+2x
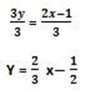
i) (1,2) and y-intercept = 2
(1,2), (0,2)
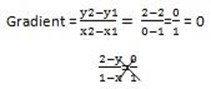
0 = 2-y
y = 2
j) (5,5) and y-intercept 0
(5,5) (0,0)
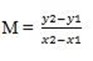
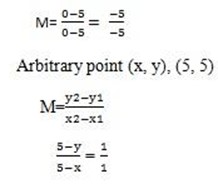
y = 5-5 + x
y=x
(2) (i) y – intercept -2 , gradient 1
(0, – 2) gradient 1
Arbitrary (x, y)
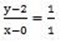
y – 0 = y + 2
x = y+2
y = – 2 + x
(ii) y-intercept 7,gradient 3/4
(0,7), (x,y) , gradient 3/4
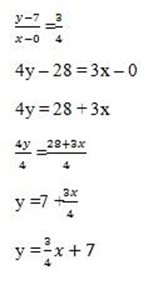
iii) y-intercept -16, gradient 4
(0,-16), (x,y) m = 4
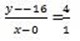
4x-0 = y +16
-y =-4x +16
y = 4x -16
y = 4x – 16
iv) y-intercept 2, gradient is -10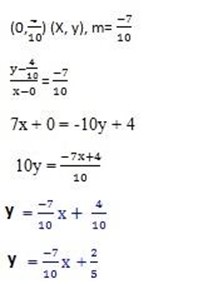
3 (i) 7x + 4y = 11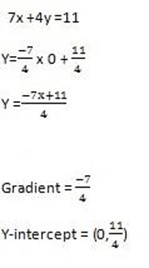
Alternatively
7x +7y = 11
4y = -7x +11
ii) 14x + 3y = 12
iii) 2x=5 +y
x=0
2x = 5 + y, y=0-5, y =-5
y = 2x -5
y =2x-5
Gradient = 2
y- intercept = (0,2)
iv) 4x +5y= 40
x=0
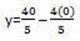
5y= -4x + 40
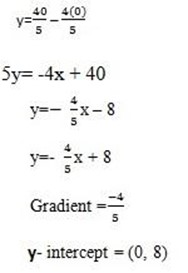
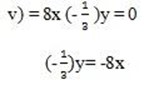
y = 24x
y = 24 (0)
y = 0
y = -8x X -3 = 24x
y = 24x + 0
Gradient = 24
y-intercept = (0,0)
vi) 6x =5-2y
x=0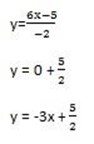 
Gradient = -3
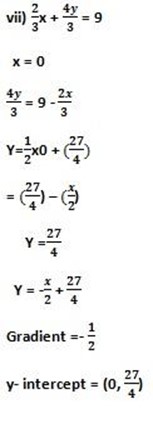
4. x-intercept , y=0
5x + 6(0) – 60 = 0
5x – 60 = 0 + 60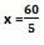
x= 12
X- intercept = (12,0)
Y- intercept, x=0
5(0) + 6y – 60 = 0
5x – 60 = 60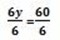
y = 10
y-intercept = (0,10)
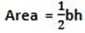
Area = 60 square units
EXERCISE 10.4
1. (i) 2x + y = 5
4x – y = 7
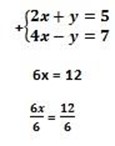
x = 2
2x + y =5
2 (2) + y = 5
4 + y = 5
y = 5-4
y = 1
x =2 and y = 1
(ii). 3x + y = 6
5x + y =6
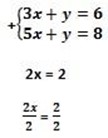
x = 1
from 3x + y = 6
3 x 1 + y = 6
3 +y = 6
y = 6-3
y = 3
x = 1 and y = 3
(iii) 5x -2y = 16
x + 2 = 8
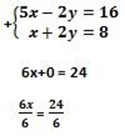
x = 4
Let find the value of y by taken equation one
5x -2y = 16
5 x 4 – 2xy =16
20 – 2y = 16
-2y = 16 – 20
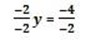
y = 2
x = 4 and y = 2
(iv) 8x + 5y = 40
9x + 5y = 5
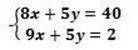
x+0 = 35
x = 35
let find the value of y by taken one equation
8 x 35 + 5y =40
280 + 5y = 40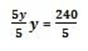
y = -48
x = 35 and y = -48
(v). 7x -4y = 17
5x -4y = 11
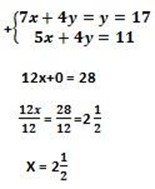
Let find the value of y taken one equation 7x – 4y = 17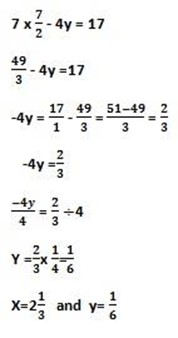
(vi) 0.7x – 0.5y = 2.5
0.7x – 03y = 2.9
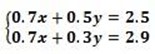
0-0.2 = -0.5
0.2y = -10.4
0.2 = -10.4
y = 2
Let find the value of x by taken one equation
0.7x – 0.5y = 2.5
0.7x – 0.5(2) = 2.5
0.7x = 2.5 + 1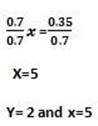
2. (i) 3x -2y = 5
2x +y = 8
3x – 2y = 5……………(i)
2x + y = 8…………….(ii)
y=8 – 2x ……………..(iii)
put eqn (iii) into (iv)
3x -2x (8 -2x) = 5
3x – 16 + 4x = 5
3x + 4x -16 =5
7x = 5 + 16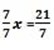
x=3
y= 8-2 x3
y= 8-6
y = 2
x =3 and y = 2
(ii) 5x + y =23
3x – 2y = 6
5x – y = 23…………(i)
3x -2y = 6………….(ii)
5x-y +y = 23 + y.
5x =23 + y
5x – 23 =y…………….(iii)
put eqn (iii) in (ii)
3x -2 (5x – 23) = 6
3x -10x + 46 = 6
-7x+ 46 = 6
7x = 6 – 46
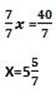
Let find the value of y by taken one equation
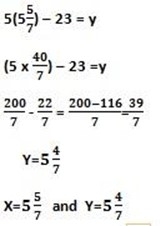
(iii). x -3y=2
4x + 2y = 36
x -3y=2 ……………(i)
4x + 2y = 36 …………(ii)
x=2 + 3y ……………..(iii)
put eqn (iii) in (ii)
4 (2 + 3y) + 2y = 36
8 + 12y +2y = 36
8 + 14y = 36
14y = 36 -8
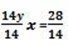
y = 2
Let find the value of x by taken one equation
x= 2 +3y
x = 2+3(2)
x = 2 +6
x = 8
y = 2 and x = 8
(iv) 7x – y = 14
8x – 2y = 16
7x – y =11……………(i)
8x – 2y = 16 …………(ii)
7x – 14 = y ………………(iii)
put eqn (iii) into eqn (ii)
8x – 2x (7x – 14) = 16
8x – 14 + 28 = 16
-6x + 28 = 16
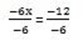
x = 2
Let find the value of y by taken one equation
y = 7 x2 = 14
y = 14 -14 = 0
y = 0
x = 2 and y =o
(v) 7x + y = 14
8x – 2y =6
7x + y =14…………….(i)
8x – 2y = 6…………… (ii)
y = 14 – 7x ……………(iii)
put eqn (iii) in (ii)
8x – 2(14 – 7x) =6
8x – 28 + 14x =6
22x – 28 = 6
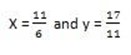
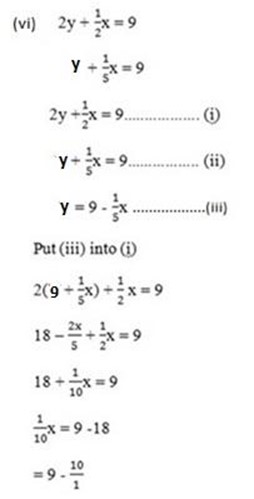
x = -90
Let find the value of y by taken one equation
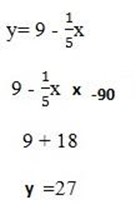
x = -90 and y = 27
3. (i) 3y – x = 4
y + 2x = 6
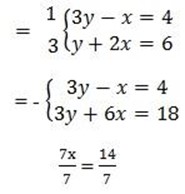
x = 2
Let find the value of y by taken one equation
y +2x = 6
y + 2 x2 = 6
y +4 =6
y = 6-4
y =2
x =2 and y = 2
(ii) 8m- n = 38
m – 3n = -1
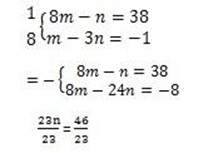
n = 2
Let find the value of m by taken one equation
m -3 = -1
m-3 X 2 = -1
m-6 = -1
m = -1 + 6
m = 6-1
m = 5
n = 2 and m = 5
(iii) 5x – 2y = 10
-x + 3y = 24
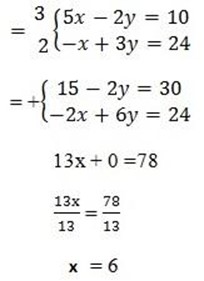
Let find the value of y by taken one equation
5 x 6 – 2y = 10
30 – 2y = 10
-2y = 10 -30
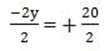
y = 10
x = 6 and y = 10
4. (i) x -y = -3
2x – y = -5
x-y = -3 ………………..(i)
2x – y = -5 …………….(ii)
x=-3 + y ……………….(iii)
put eqn (iii) into eqn (ii)
2(-3 + y) – y= -5
-6 + 2y – y = -5
y – 6 = -5
y = -5 + 6
y = 1
x = -3 + y
= -3 +1
x = -2
x= -2 and y = 1
(ii). x -2y = 6
x + 2y = 2
x – 2y = 6 ………………..(i)
x + 2y = 2 ……………….(ii)
x =6 + 2y ………………..(iii)
put eqn 3 into eqn 2
6 + 2y +2y = 2
6 + 4y = 2
4y = 2 -6
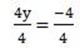
y = -1
x = 6 + 2x -1
x = 6 + -2
x= 4
x = 4 and y = -1
(iii) 3x – 4y = -11
2x + 3y = 16
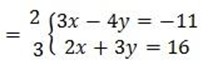
6x -4y = -11 ………………(i)
6x + 3y = 16………………(ii)
6x = -11 + 4y …………….(iii)
put eqn (iii) into (ii)
-11 + 4y + 3y = 16
-11 + 7y = 16
7y = 16 +11
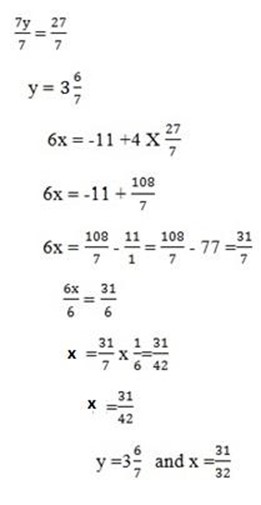
(iv) 2x – 3y = 32
3x – 4y = 30
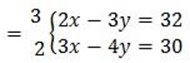
6x – 9y =96…………..(i)
6x – 8y = 60…………..(ii)
6x = 96 + 9y ………….(iii)
put eqn (iii) into eqn (ii)
96 + 9y -8y =60
96 + y =60
y = 60 – 96
y= -36
6x = 96 +9x -36
6x = 96 – 324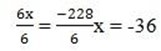
x = -38 and y = -36
(v) 5a -5b = 7
2a – 4b = 2
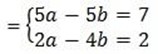
10a-5b =7 ………….(i)
10a -4b = 2 ………….(ii)
10a = 7 + 5b ………….(iii)
put eqn (iii) into eqn (ii)i
7 +5b -4b= 2
7 + b =2
b =2-7
b = -5
10a = 7+5x -5
10a = 7 + -25
10a =7 – 25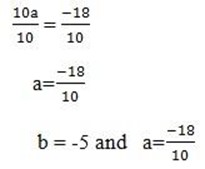
5. (i) 10u + 3v – 4 = 0
6u + 2v – 2 = 0
10u + 3v = 4
6u + 2v = 2
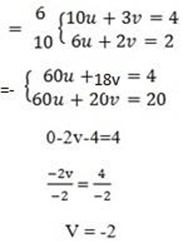
let find the value of u by taken equation
10u + 3v =4
10u + 3 (-2) = 4
10u -6 = 4
10u = 4 +6
10u = 10
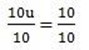
v = -2 and u = 1
(ii) x – y = 1
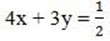
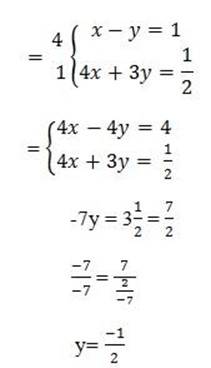
let find the value of x by taken one equation
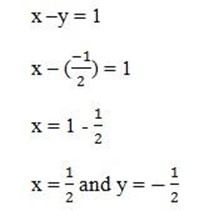
(iii) 3x + 3y =15
2x + 5y = 14
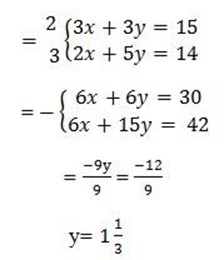
Let find the value of x by taken one equation
3x + 3y =15
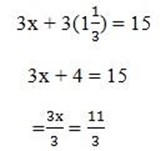
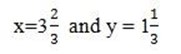
(iv) 7x -3y = 15
5x – 2y = 19
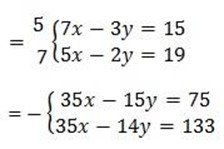
y = 58
Let find the value of x taken one equation
7x -3y =15
7x – 3 x 68 = 15
7x – 204 =15
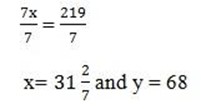
(v). x + y =5
x – y =1
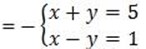
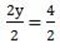
y = 2
Let find the value of x by taken one equation
x + y = 5
x + 2 = 5
x= 5-2
x = 3
x = 3 and y = 2
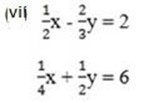
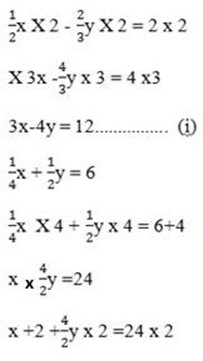
2x + 4y = 48………………… (ii)
Now you can take equation (i) and (ii) to solve the equation
3x-4y =12
2x+ 4y = 48
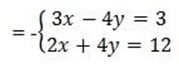
x = -9
Let find the value of y by taken one equation
3x – 4y =3
3(-9) -4y = 3
-27 – 4y = 3
-4y = 3 + 27
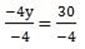
y = -7.3 and x = – 9
EXERCISE 10.5
1. Let the numbers be x and y
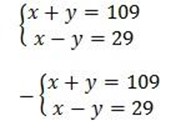
2y = 80
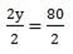
y = 40
let find the value of x
x + y = 109
x + 40 = 109
x = 109 – 40
x = 69
The two numbers are 69 and 40
2. let the first number be x
let the second number be y
x + 3y = 1 ……………(i)
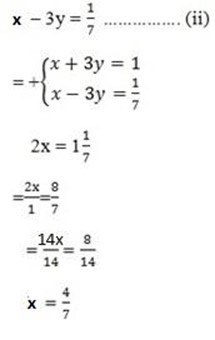
Let find the value of y
x+3y =1
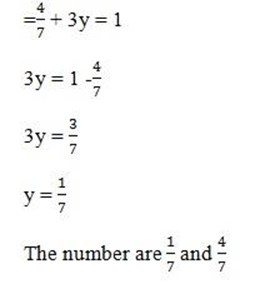
3. Let the girls number be x and the boys be y
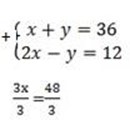
x = 16
let find the value of x
x + y = 36
16 + y = 36
y = 20
The girls are 16 and boys are 20
4. let the length be x and the width be y
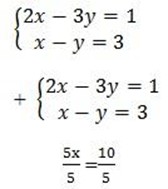
Let find the value of y
2x -3y = 1
2 x 2 -3y = 1
4 – 3y = 1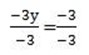
y = 1
The length =2cm and width = 1cm
5. Let the pencils be x and pen be y
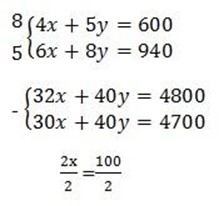
x = 50
Let the value of x
4x + 5y = 600
4 x 50 + 5y = 600
200 +5y = 600
5y =600 -200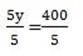
y = 80
The pencils are 50 and pens are 80
6. let paul,s money be x
let john’s money be y
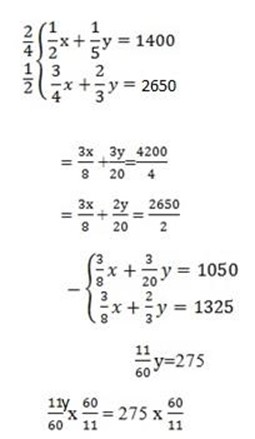
y = 1500
Let find the value of x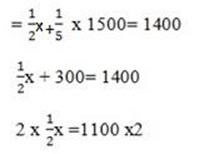
x = 2200
Paul’s money = 2200 shs and John’s money = 1500 shs
7. let the price of the sheep be a
Let the price of goat be = b
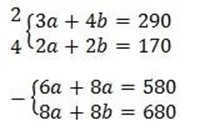
2a = 100
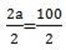
a = 50
let find the value of b
3a + 4b = 290
3 x 50 + 4b = 290
150 + 4b = 290
4b = 290 – 150
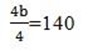
b = 35
The price of sheep = a
The price of goat = b
They bought 1 goat at 35 shs and 1 sheep at 50shs
