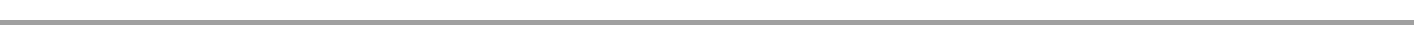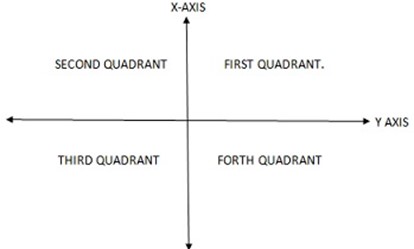
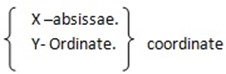
Exercise
1. Plot the following point. P (2,2), T (-1, -2), L (2, -1)
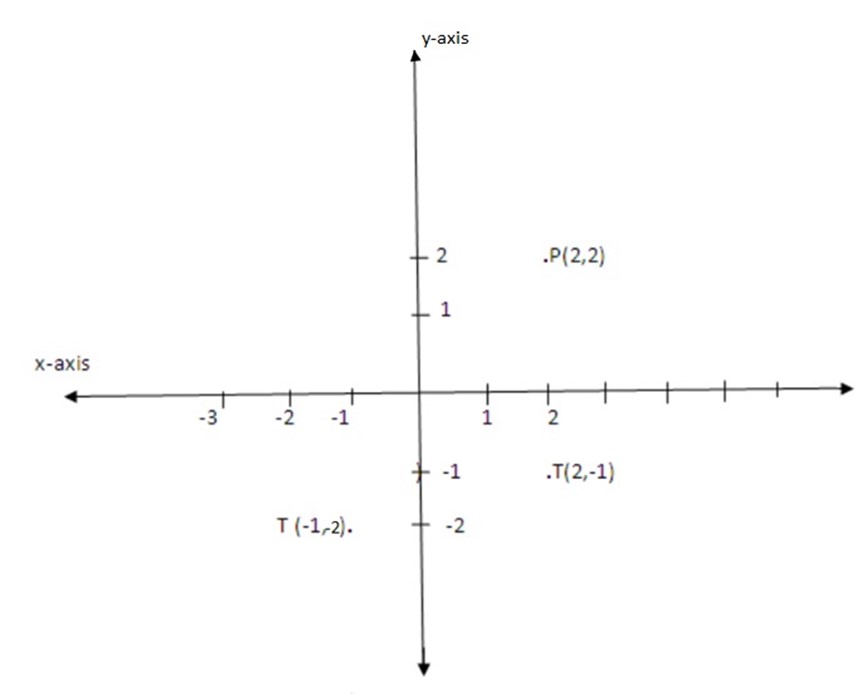
2. In which quadrants is the?
a. Abscissa positive? I
b. Ordinate negative III
c. Abscissa negative II
d. Ordinate positive I
e. Abscissa negative and ordinate negative? III
EQUATIONS IN A STRAIGHT LINE
Gradient / slope
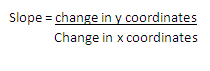
Equation
A (3,2) N (x,y) m=1
Gradient =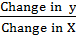 
1 =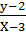 
y – 2 = x – 3
y =x – 3 + 2
y=x – 1
Consider two points P (x, y) and (X2, Y2) are given and lie on the same line.
If there exists point N (x, y) which lies on PQ, where X1 ≠ X2 the N lies on the same line If and Only if the slope of PN if the same as the slope of PQ.
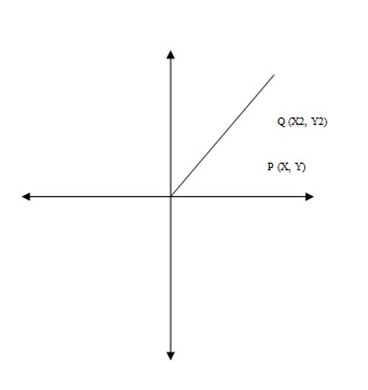
Slope PQ =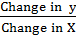 
P(x ,y) and Q ( X2, Y2)
Slope of PQ (M) =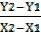 
Slope at PN =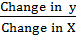 
P(X ,Y) and N ( X, Y)
M =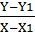 
Exercise
1. A straight line is drawn through (2, 4) and (-2, 2) . Draw a graph to find where it intersects.
a. The y- axis
b. The x-axis
Solution:
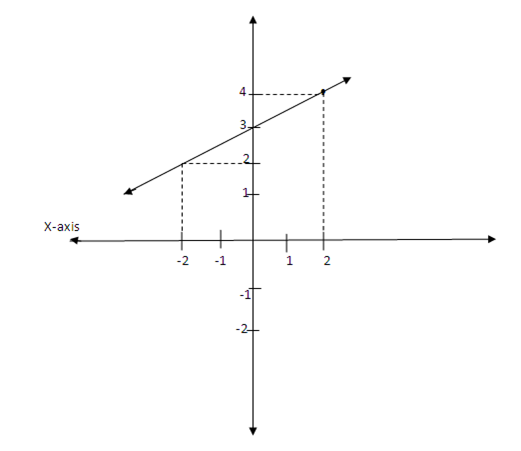
(a) (0 , 3)
(b) (-6, 0)
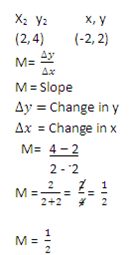
Equation of line
Choose the points (2, 4)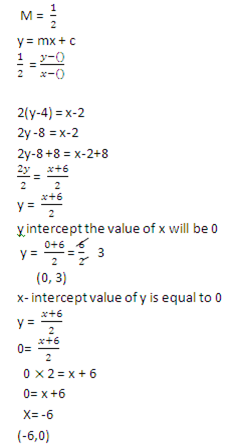
Will intersect in point (-6, 3)
2. In figure below, find the coordinates of the following points; A,P and L
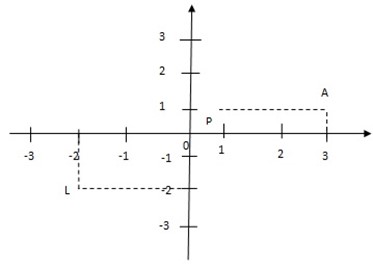
A (3, 1), P (0,0) , L(-2,-2)
3. Find the gradient of the straight line joining each of the following pairs of points.
a. (1,6) and (5,7)
b. (3,2) and (7,-3)
c. (-3,4 ) and (8,1)
Solution: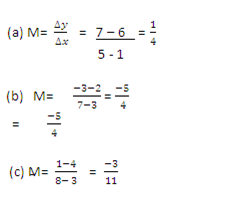
4. Find the equation of the line of 2 which passes through the point (3,5)
Solution;
M = 2
M =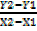 
2=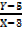 
2X – 6 = Y – 5
2X – 6 + 5 = Y
Y=2X – 1
5. For each of the following conditions, find the equations of the line.
a. Passing through points (4,7) having gradient of 3.
b. Passing through point (4,7) and (3,4)
c. Passing through A (4,-3) whose slope is 2/5 of the slope of the line joining A (4,-3) to B (9,7)
Solution
a). 3 = Y-7
X-4
3X-12= Y-7
Y=3X-5
b). M= 7-4
4-3
M=3
3=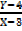 
3X – 9 = Y – 4
Y =3X – 5
c). M=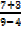 
= 2
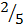x 2=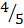 
= 
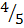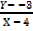
4X – 16 – 15 = 5Y
Y=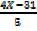 
6. Verify that the points (-2,2) and ( -6,0) lie on the line joining points A (-4,1) and B (2,4).
Solution
M =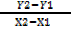 
= 
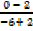
M=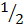 
Also
M = 
M=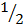 
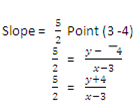
7. Find the equations of the following straight lines in the form of ax + by + c = 0
a. The line joining the points ( 2,4) and (-3,1)
M=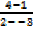 
= 
= 
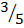
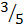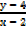
5y – 20 = 3x-6
5y = 3x + 14
3x – 5y + 14 = 0
b. The line through (3,1) with gradient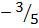 
Solution:
M=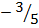 
M =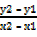 
= 
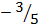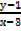
-3x + 9 -5y + 5 = 0
-3x – 5y + 14 = 0
(c) = The line through (3,-4) and which has the same slope as the line 5x-2y =3
5x-2y = 3
5x – 3 = +2y
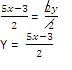
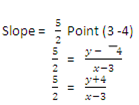
2y + 8 = 5x + -15- 8
2y +8 -8 = 5x-15-8
2y = 5x-23
0= 5x-2y-23
. : 5x – 2y -23 = 0
8. Determine the value of K in order the line whose equation is Kx – y + 5 passes through that point (3,5)
Solution:
Kx – y+5=0
Kx-5+5=0
3K=0
K=0
9. What must be the value of T to allow the line represented by the equation 3X-Ty=16 to pass through the point (5,-4)
Solution
3x-Ty=16
3(5) – Tx-4=16
15 + 4T=16
4T = 1
T =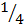 
10. Find the equation of a line with a slope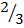 
having the same Y-intercept as the line
2x – 5y + 20 = 0
Solution:
y = mx +c
5y=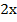 
+ 20
y= 
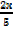+ 4
y – intercept x = 0
y = 4
points (0 , 4)
y = m(x – x1) + y1
y = 
(x – 0) + 4
y = 
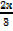+ 4
11. Determine the value of m and c so that the line Y = mx + c will pass through the points (-1, 4) and (3, 5).
Solution:
M =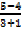 
= 
M = 
= 
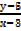
x – 3 = 4y – 20
x + 17= 4y
y =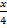 
+ 
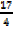
c =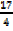 
Therefore gradient (M) = 
and c =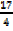
EQUATION OF A STRAIGHT LINE.
Slope of PQ (M) =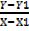 
Y-Y1 = M(X-X1)
Y= MX – MX1+ Y1
Y = MX + C
Example
(3, 5) slope = 2
Y – 5 = 2(X-3)
Y= 2x – 6 + 5
Mid point of a straight line
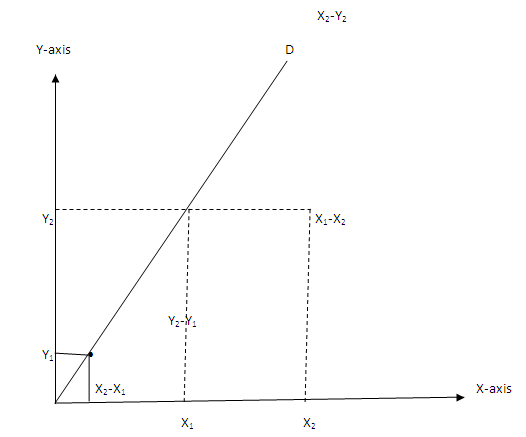
Similarities;
= 
= 
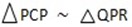
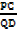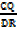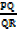
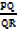= 1
Take;
PC = PQ
QD QR
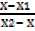= 1
X-X1 = X2– X
2X= X1 + X2
X =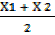 
= 
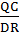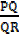
QR
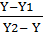= 1
2Y = Y2 + Y1
Y=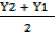 
Mid point (x, y) =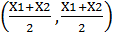 
EXERCISE
1. Find the coordinates of the mid points joining each of the following pairs.
a. (7,1) and (3,5)
Midpoint =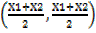 
= 
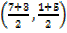
= (5, 3)
b. ( 0,0 ) and (12, 3)
Mid point =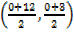 
= (6, 1.5)
DISTANCE BETWEEN TWO POINTS
PQ2= PC 2 + BC2
PQ2 = (X-X1)2 + (Y- Y1)2
= 
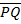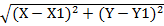
EXERCISE
1. If the line from (-4, Y1) to (X2, -3) is bisected at (1,-1) . find the values of Y1 and X2
Solution
1= (-4 + X2)/2
2
2 = -4 + X2
X2 = 6
-1 = Y -3
2
-2 = Y1 + -3
Y1 = 1
2. The mid point of a line segment is ( -2,5) and one end point is (1,7) . Find the other end point.
Solution:
Mid point =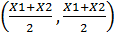 
= 
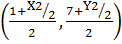
-2 =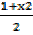 
-4 = 1 + X2
X2 = -5
5 =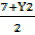 
10 = 7 + Y2
Y2 = 3
The other points is (-5 , 3)
3. The mid points of the sides of a triangle are ( 2 , 0) and (4, -3 ½ ) and
(6 , ½) .Find the vertices of the triangle if one of them is (4,3) .
Solution
i. Mid point = (2,0)
2 = 4 + X2
2
4 = 4+ X2
X2 = 0
0 = 3+ Y2
2
Y2 = -3
ii.4 = 4+ X2
2
X2= 8-4
X2= 4
-3.5 = 3 + Y2
2
Y2 = -7-3
Y2 = -10.
iii. 6 = 4+ X2
2
12 = 4 + x2
X2 = 8
0.5 = 3 + Y2
2
1= 3 + y2
Y2 = –2
:. The vertices of the triangle are (0 , -3), (4 , 10) and (8 , -2)
4. Three vertices of a parallelogram ABCD are A (-1,3) ,B(2,7) and C (5,-7). Find the coordinates of vertex D using the principle that the diagonals dissect each other.
Solution:
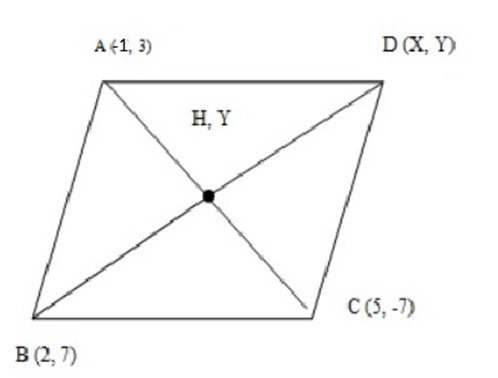
Mid point H (x, y) = (5-1 ) , (-7+3)
2 2
= (2,-2)
(2,-2) = 2+ X, 7+Y
2 2
4 = 2+ X
X = 2
-4 = 7 + Y
Y= -11
D= ( 2,-11)
EXERCISE
1.Find the distance between the line segments joining each of the following pairs of points.
a. (1,3) and (4,7)
Solution
D =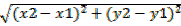 
D =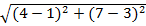 
D =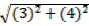 
D =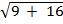 
D=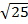 
D = 5
b. (1,2) and (5,2)
Solution;
D =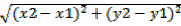 
D =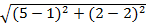 
D =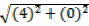 
D =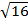 
D = 4
2.Find the distance of the following point from the origin.
(-15, 8) (0, 0)
Solution
D =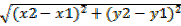 
D =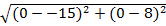 
D =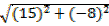 
D =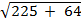 
D=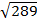 
D = 17
3. P, Q, R are the points (5,-3) (-6,1) (1,8) respectively . Show that triangle PQR is isosceles
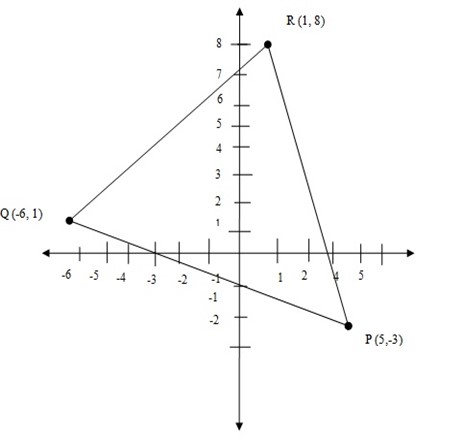
QP =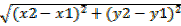 
QP =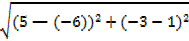 
QP =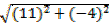 
QP =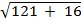 
QP=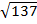 
PR =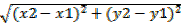 
PR =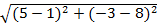 
PR =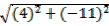 
PR =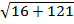 
PR=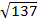 
Therefore triangle PQR is isosceles
PARALLEL LINES
Two lines are parallel if they have the same slope.
Example
1. Find whether AB is parallel to PQ in the following case.
a. A( 4,3) , B (8,4) P ( 7,1) Q ( 6,5)
Solution
Slope of AB = Change in Y
Change in X
= 
= 
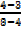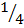
Slope of PQ=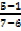 
= -4
Therefore AB and PQ are not parallel line
2. Find the equation of the line through the point ( 6,2) and parallel to the line
X +3Y – 13=0
Solution
X+3Y -13 =0
3Y = -X+13
Y= -X/3 + 13/3
Slope = -1/3
Equation of a straight line
Y – Y1= M (X-X1)
Y – 2 = -1/3 (x-6)
Y = -x/3 + 4
3. Show that A (-3, 1), B (1,2) , C( 0,-1) and D ( -4,-2) are vertices of a parallelograms.
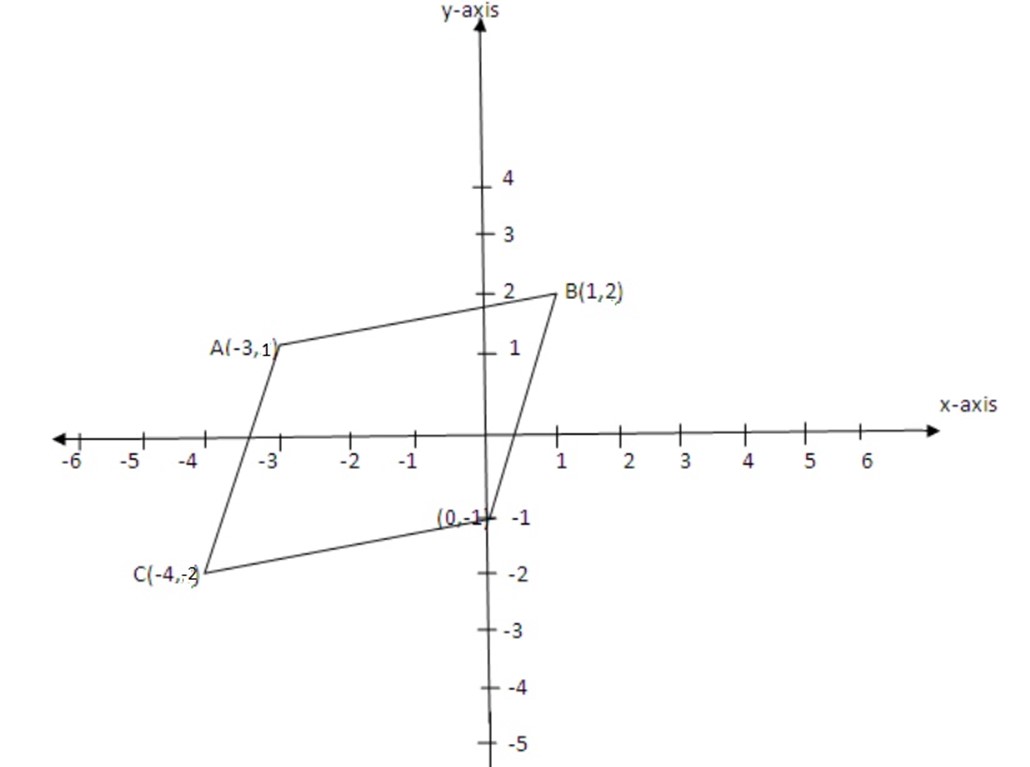
Slope AB =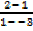 
= 
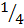
Slope CD =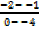 
= 
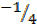
PERPENDICULAR LINES
Two lines are perpendicular if they intersect at right angle. Suppose that two lines L1 and L2 are perpendicular with slopes M1 and M2 as shown below.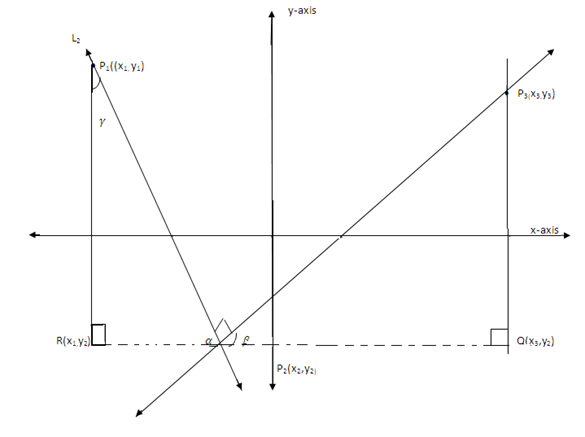
Choose Point P(x1,y1) , P2(x2, y2) P3(x3, y3), R and Q
Also ∝, β and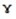 
are the Greek letters Alpha, beta and gamma respectively representing the degree measures of the triangles as indicated. Then
If two non-vectorlines are perpendicular with slopes M1 and M2,then
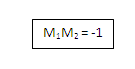
Two lines are perpendicular if they intersect at right angles.
If two non vertical lines are perpendicular with slopes M1 and M 2, then
M1 x M 2 = 1
Example
1. Find the equation of the line through P (-2 , 5) and perpendicular to the line
6X – 7Y = 4
Solution
y = mx + c
From the equation we get
Y = (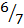
)X –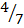 
M1 =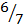 
M1 x M2 = -1
(
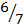) M2= -1
M2= –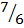
Equation M = –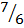
(-2, 5)
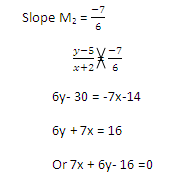
2. Find the equation of the line through the point (6,2) and perpendicular to the line joining P ( 3,-1) and Q ( -2 ,1)
Solution:
Slope of P and Q = 1- -1 = –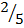
-2-3
M1 x M 2 = -1
M2= -1 x -5/2 = 5/2
Equation M = 5/2 (6,2)
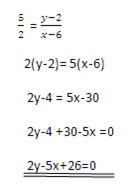
3. Find the equation of a line perpendicular to the equation 3X- 11Y -4 = 0
And passing through (- 3, 8)
Solution:
3X – 11Y – 4 =0
Y =mx + c
-11y = -3X +4
Y= 3/11 X – 4/11
M = 3/11
M2 = – 11/3
Equation M = –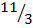
( -3,8)
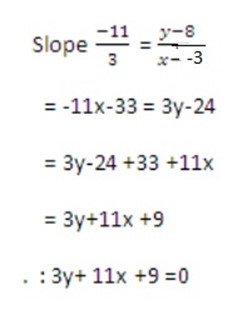
4. Show that A (-3 , 2) , B ( 5 , 6) and C (7 , 2) are vertices of a right angled triangle.
Solution
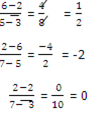
Slope of AB x slop of BC = -1
Hence AB is perpendicular to BC
5. Determine which two sides of the following triangles ABC contain a right angle. A(3,2) , B ( 5,-4) , C ( 1, -2)
Solution
Slope AB = -4 – 2 = -6 = -3
5-3 2
Slope BC = -2 + 4 = 2 = – 1 = 1
1-5 -4 2 2
Slope AC = –2-2 = –4 = 2
1-3 -2
Slope of AB x slope of AC = -1
-(1/2) x 2 = -1
Therefore AB is perpendicular to AC
