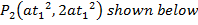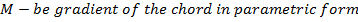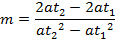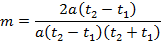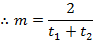ADVANCED MATHEMATICS FORM 6 – COORDINATE GEOMETRY II

GENERAL EQUATION OF THE PARABOLA

·         Consider the parabola whose focus is s (u, v) and directrix ax + by + c = 0

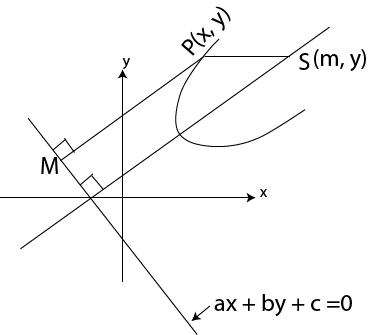
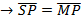
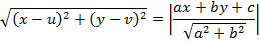
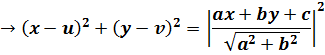
          Is the general equation of the parabola

Where;

     S (u, v) – is the focus

          Examples:

1.  Find the focus and directrix of the parabola y² = 8x

Solution

Given y² = 8x

  Comparing from

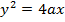
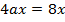
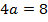
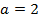
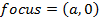
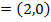
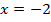
2.  Find the focus and the directrix of the parabola

y² = -2x

Solution

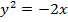
Compare with

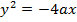
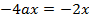
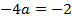
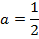
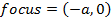
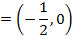
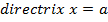
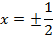
3.  Find the focus and directrix of x² = 4y

Solution

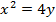
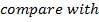
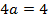
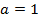
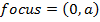
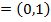
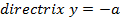
4. Given the parabola x² =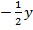

a) Find i) focus

ii) Directrix

iii) Vertex

b) Sketch the curve

Solution

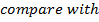
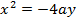
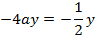
i) Focus =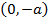

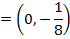
ii) Directrix, y = a

iii) Vertex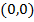

b) Curve sketching

         

5.  Find the equation of the parabola whose focus is (3, 0) and directrix

X = -3

        Solution

          Given focus (3, 0)

          Directrix, x = -3

          (3, 0) = (a, 0)

          From

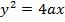
y² = 4 (3)x

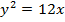
6.   Find the equation of the parabola whose directrix, y =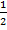

Solution

Given directrix, y =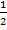

Comparing with

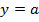
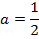
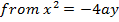
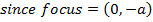
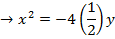
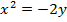
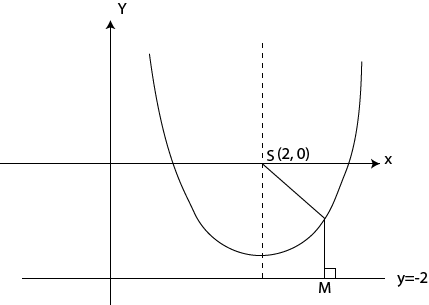
7.  Find the equation of the parabola whose focus is (2, 0) and directrix, y = – 2.

Solution

Focus = (2, 0)

Directrix y = -2

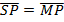
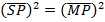
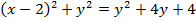
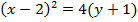
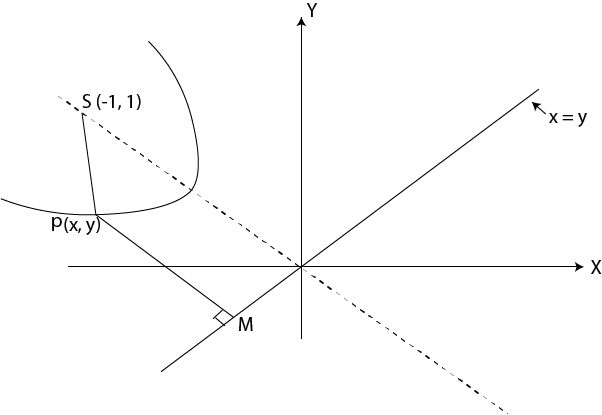
8.   Find the equation of the parabola whose focus is (-1, 1) and directrix x = y

Solution

Given: focus = (-1, 1)

Directrix x = y

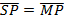
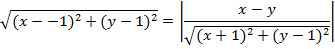
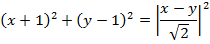
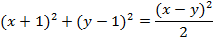
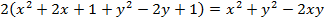
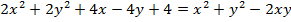
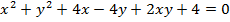
PARAMETRIC EQUATION OF THE PARABOLA
The parametric equation of the parabola  are given

X = at² and y = 2at

          Where;

          t – is  a parameter

 TANGENT TO THE PARABOLA

Tangent to the parabola, is the straight line which touches it at only one point.

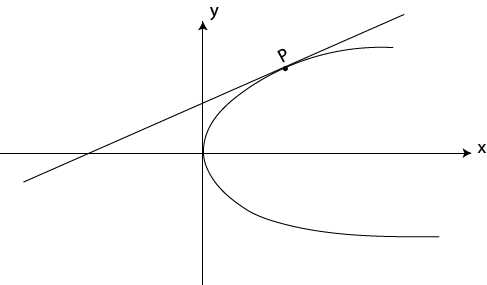
Where, p – is the point of tangent or contact

CONDITIONS FOR TANGENT TO THE PARABOLA

a) Consider a line y = mx + c is the tangent to the parabola y² = 4ax². Hence the condition for tangency is obtained is as follows;

i.e.

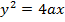
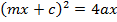
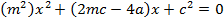
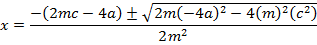
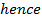
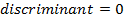
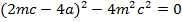
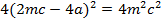
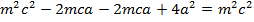
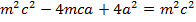
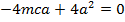
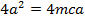
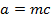
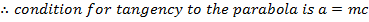
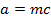
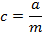
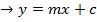
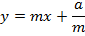
b) Consider the line ax + by + c = is a tangent to the parabola y² = 4ax Hence, the condition for tangency is obtained as follows;

i.e.

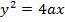
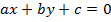
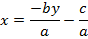
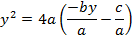
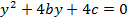
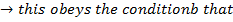
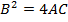
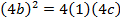
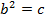
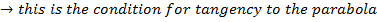
Examples

1.  Prove that the parametric equation of the parabola are given by

X = at², and y = 2at

Solution

Consider the line

Y = mx + c is a tangent to the parabola y² = 4ax. Hence the condition for tangency is given by y² = 4ax

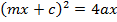
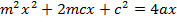
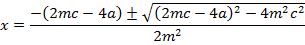
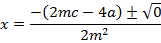
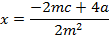
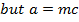
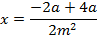
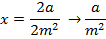
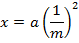
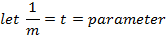
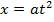
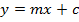
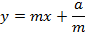
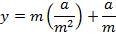
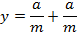
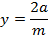
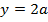
The parametric equation of the parabola of m is given as x = at² and y = 2at

Where;

t – is a parameter

GRADIENT OF TANGENT OF THE PARABOLA

The gradient of tangent to the parabola can be expressed into;

i) Cartesian form

ii) Parametric form

i) IN CARTESIAN FORM

– Consider the tangent to the parabola y² = 4ax Hence, from the theory.

Gradient of the curve at any = gradient of tangent to the curve at the point

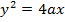
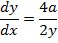
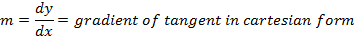
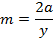
ii) IN PARAMETRIC FORM

Consider the parametric equations of the parabola

 i.e.

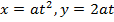
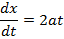
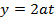
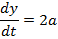
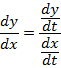
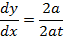
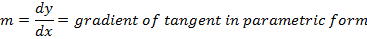
EQUATION OF TANGENTS TO THE PARABOLA

These can be expressed into;

i) Cartesian form

ii) Parametric form

i) In Cartesian form

– Consider the tangent to the parabola y² = 4ax at the point p (x, y)

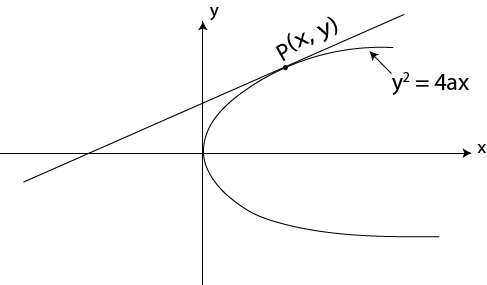
Hence the equation of tangent is given by

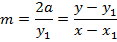
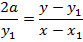
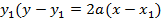
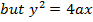
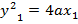
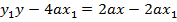
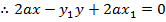
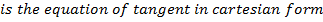
ii) In parametric form

·         Consider the tangent to the parabola y² = 4ax at the point p (at², 2at)

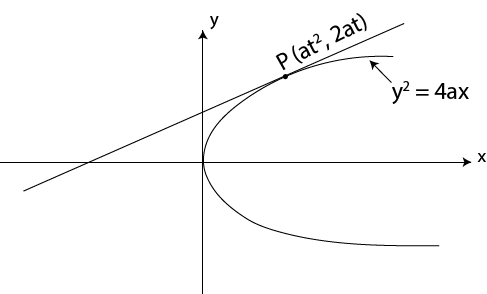
Hence the equation of tangent is given by;

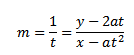
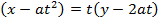
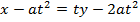
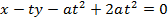
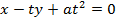
Examples

1. Show that the equation of tangent to the parabola y² = 4ax at the point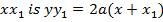   

2. Find the equation of tangent to the parabola y² = 4ax at (at², 2at)

NORMAL TO THE PARABOLA

Normal to the parabola is the line which is perpendicular at the point of tangency.

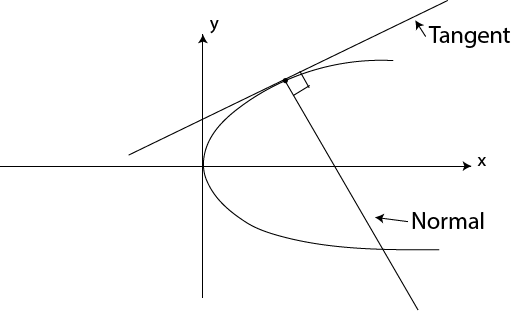
Where;

P is the point of tangency

GRADIENT OF THE NORMAL TO THE PARABOLA

This can be expressed into;·

i) Cartesian form

ii) Parametric form

i) In Cartesian form

– Consider the gradient of tangency in Cartesian form

i.e.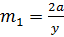

Let M = be gradient of the normal in Cartesian form but normal is perpendicular to tangent.

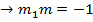
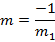
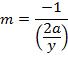
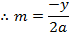
ii) In Parametric form

 Consider the gradient of tangent in parametric form.

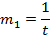
Let m be gradient of the normal in parametric form.

But

Normal is perpendicular to the tangent

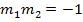
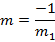
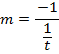
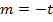
EQUATION OF THE NORMAL TO THE PARABOLA

These  can  be expressed into;·
i) Cartesian form

ii) Parametric form

i) In Cartesian form

Consider the normal to the point y²= 4ax at the point p (x₁, y₁) hence the equation of the normal given by;

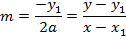
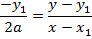
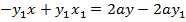
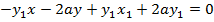
ii) In parametric form

Consider the normal to the parabola y² = 4ax at the point p (at², 2at). Hence the equation of the normal is given by;

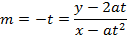
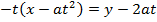
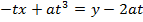
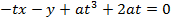
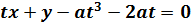
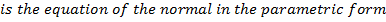
Examples:

1.  Find the equation of the normal to the parabola y² = 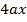 at the point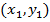

2. Show that the equation of the normal to the parabola y² = 4ax at the point (at³, 2at) is

CHORD TO THE PARABOLA

·         This is the line joining two points on the parabola

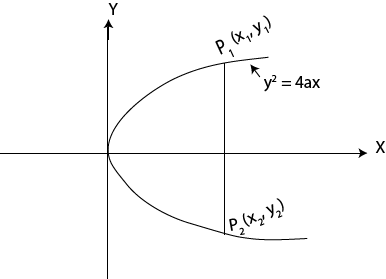
Let m – be gradient of the chord
Hence

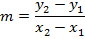
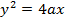
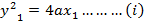
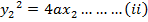
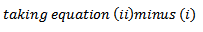
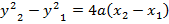
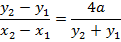
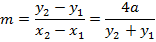
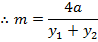
ii) GRADIENT OF THE CHORD IN PARAMETRIC FORM
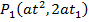Consider a chord to the parabola  at the points  and