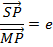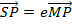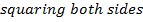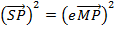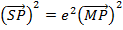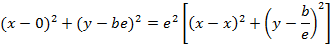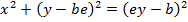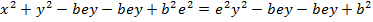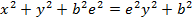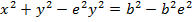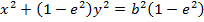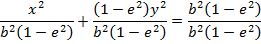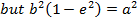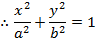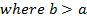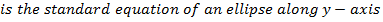ADVANCED MATHEMATICS FORM 6 – COORDINATE GEOMETRY II

EQUATION OF THE CHORD TO THE PARABOLA.

These can be expressed into;·
i) Cartesian form
ii) Parametric form

i) EQUATION OF THE CHORD IN PARAMETRIC FORM

– Consider the chord to the parabola y² = 4ax at the points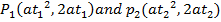. Hence the equation of the chord is given by;

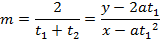
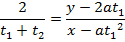
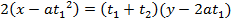
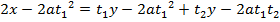
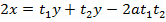
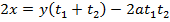
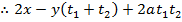
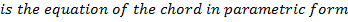
II. EQUATION OF THE CHORD IN CARTESIAN FORM.

Consider the chord to the parabola y² = 4ax at the point P₁(x₁, y₁) and P₂ (x₂, y₂) hence the equation of the chord is given by

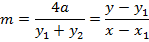
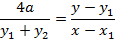
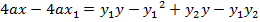
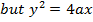
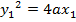
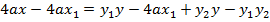
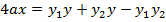
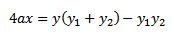
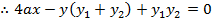
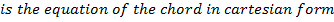
EXCERSICE.

1.  Show that equation of the chord to the parabola y² = 4ax at (x₁, y₁) and (x₂, y₂) is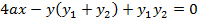

2.  Find the equation of the chord joining the points (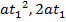) and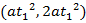

3.  As 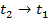_, the chord approaches the tangent at t_1.deduce the equation of the tangent from the equation of the chord to the parabola y² = 4ax.

THE LENGTH OF LATUS RECTUM

Consider the parabola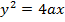

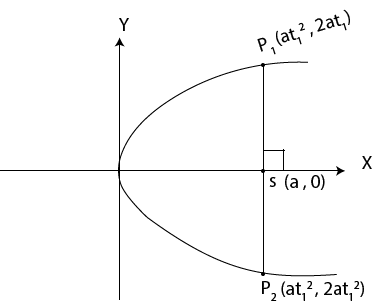
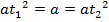
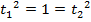
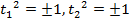
          Now consider another diagram below

Therefore, the length of latus rectum is given by

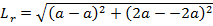
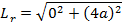
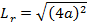
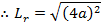
EQUATION OF LATUS RECTUM
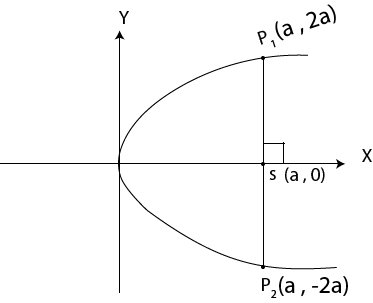
– The extremities of latus rectum are the points p₁ (a, 2a) and

p₂ (a₁, -2a) as shown below

Therefore, the equation of latus rectum is given by







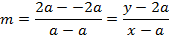
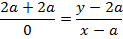
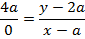
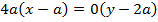
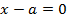
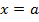
OPTICAL PROPERTY OF THE PARABOLA
Any ray parallel to the axis of the parabola is reflected through the focus. This property which is of considerable practical use in optics can be proved by showing that the normal line at the point ”p” on the parabola bisects the angle between 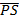 and the line  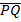which is parallel to the axis of the parabola.
Angle of INCIDENCE and angle of REFLECTION are equal

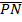– is the normal line at the point ‘p’ on the parabola
i.e.























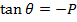
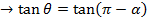
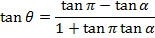
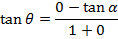
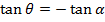
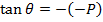
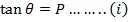
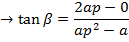
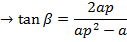
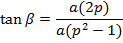
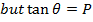
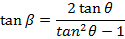
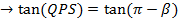
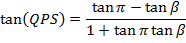
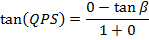
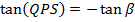
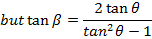
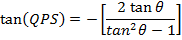
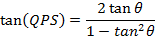
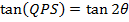
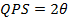
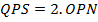            Note that;  (QPS) Is an angle.


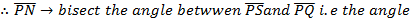
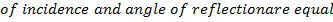
Examples

Prove that rays of height parallel to the axis of the parabolic mirror are reflected through the focus.

TRANSLATED PARABOLA

1. 

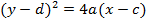
– consider the parabola below

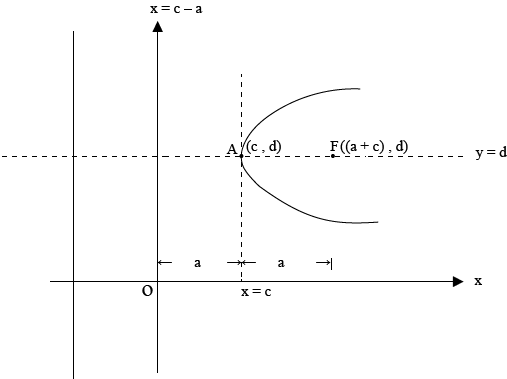
PROPERTIES.

I) The parabola is symmetrical about the line y = d through the focus
II) Focus,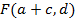
III) Vertex,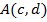
IV) Directrix,

2.  

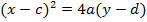
– Consider the parabola below

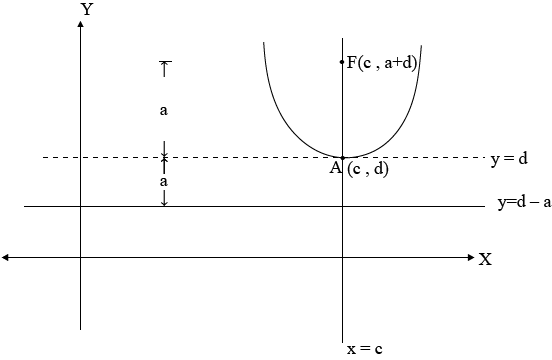
PROPERTIES

I) the parabola is symmetrical about the line x = c, through the focus
II) Focus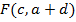
III) Vertex,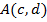
IV) Directrix,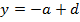

Examples

1. Show that the equation 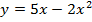 represent the parabola and hence     find

i) Focus

ii) Vertex

iii) Directrix

iv) Length of latus rectum

Solution

Given;

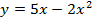
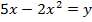
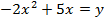
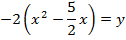
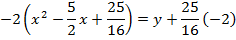
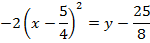
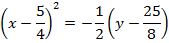
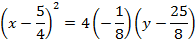
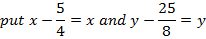
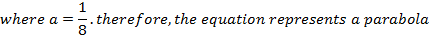
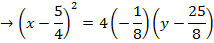
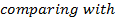
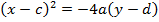
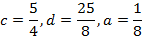
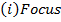
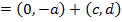
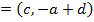
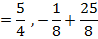
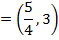
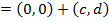
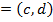
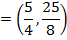
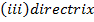
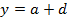
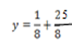
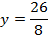
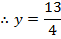
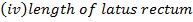
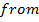
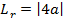
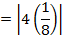
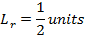
2. Shown that the equation x² + 4x + 2 = y represents the parabola hence find its focus.

Solution

Given;

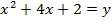
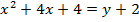
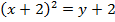
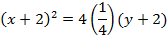
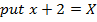
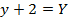
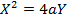
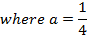
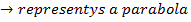
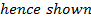
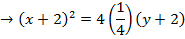
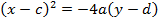
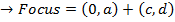
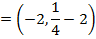
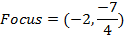
3.  Show that the equation x² + 4x – 8y – 4 = 0 represents the parabola whose focus is at (-2, 1)

          Solution

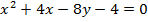
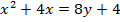
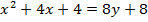
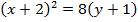
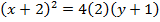
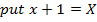
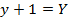
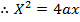
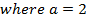
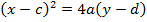
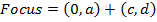
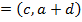
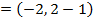
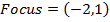
ELLIPSE

This is the conic section whose eccentricity e is less than one

I.e. |e| < 1

         

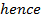
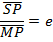
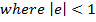
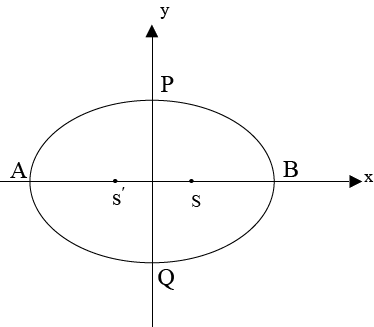
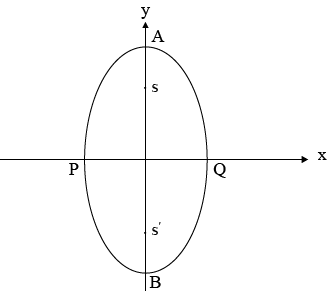
AXES OF AN ELLIPSE

An ellipse has two axes these are
i) Major axis
ii) Minor axis

1.  MAJOR AXIS

Is the one whose length is large

2.   MINOR AXIS

Is the one whose length is small

a)

b)

Where

AB – Major axis

PQ – Minor axis

EQUATION OF AN ELLIPSE
These are;
i) Standard equation

ii) General equation

1.   STANDARD EQUATION

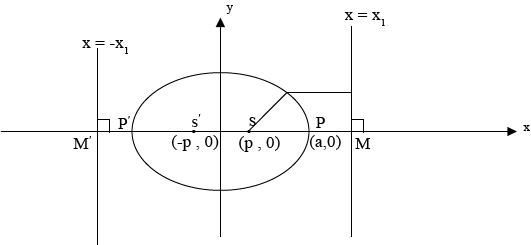
– Consider an ellipse below;

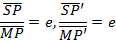
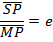
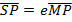
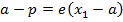
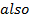
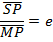
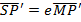
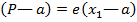
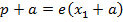
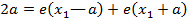
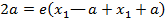
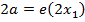
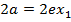
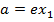
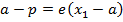
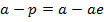
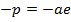
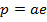
1^st CASE
Consider an ellipse along x – axis

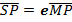
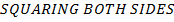
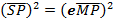
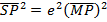
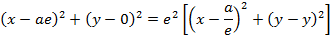
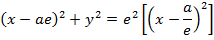
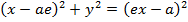
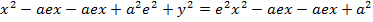
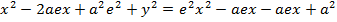
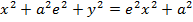
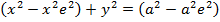
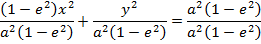
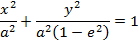
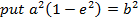
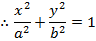
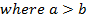
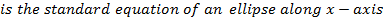
PROPERTIES

I) an ellipse lies along the x – axis (major axis)

ii) a > b

iii)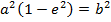

iv) Foci,

v)  Directrix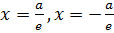

vi) Vertices, (a, o), (-a, o) along major axis

(0, b) (0, -b) along minor axis

vi) The length of the major axis l major = 2a

viii) Length of minor axis l minor = 2b

Note:

For an ellipse (a – b) the length along x – axis

B – is the length along y – axis

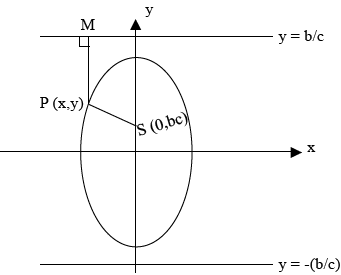
2^nd CASE

·         Consider an ellipse along y – axis