ADVANCED MATHEMATICS FORM 6 – COORDINATE GEOMETRY II

GRADIENT OF THE NORMAL TO AN ELLIPSE.

This can be expressed into two
i) Cartesian form
ii) Parametric

I) IN CARTESIAN FORM

– Consider the gradient of the tangent in Cartesian form

But normal tangent

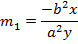
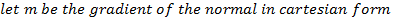
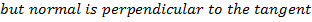
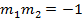
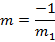
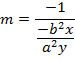
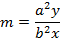
II) IN PARAMETRIC FORM
Consider the gradient of tangent in parametric form

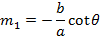
Let m = slope of the normal in parametric form



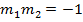
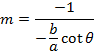
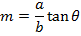
EQUATION OF THE NORMAL TO AN ELLIPSE
This can be expressed into;
(i) Cartesian form
(ii)  Parametric form

I. IN CARTESIAN FORM

– consider the normal to an ellipse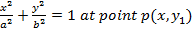

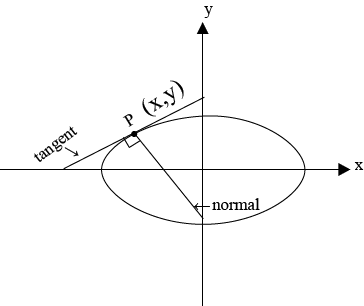
Hence the equation of the normal is given by

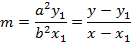
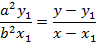
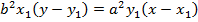
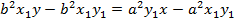
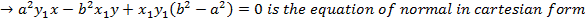
II) IN PARAMETRIC FORM
Consider the normal to an ellipse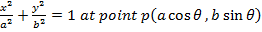

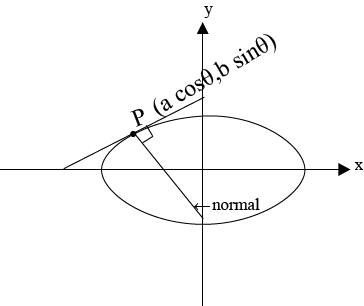
Hence the equation of the normal is given by









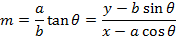
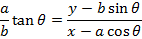
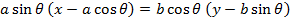
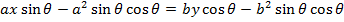
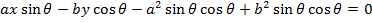
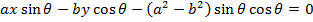
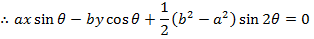
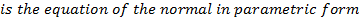
Examples
·         Show that the equation of the normal to an ellipse

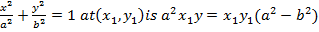
CHORD OF AN ELLIPSE.

This is the line joining any two points on the curve ie (ellipse)

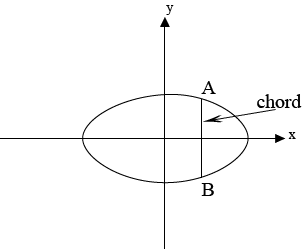
GRADIENT OF THE CHORD TO AN ELLIPSE.

This can be expressed into
i) Cartesian form
ii) Parametric form

I.  IN CARTESIAN FORM

– Consider the point A (x₁, y₁) and B (x₂, y₂) on the ellipse 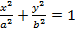 hence the gradient of the cord is given by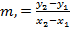       

II. IN PARAMETRIC FORM

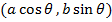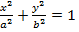Consider the points A  and B  on the ellipse  Hence the gradient of the chord is given by;

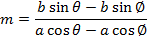
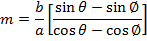
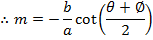
EQUATION OF THE CHORD TO AN ELLIPSE

These can be expressed into
i) Cartesian form
ii) Parametric form

I:  IN CARTESIAN FORM.

Consider the chord the ellipse 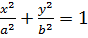at the point A (x₁, y₁) and B(x₂,y₂). Hence the equation of the chord is given by;

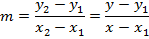
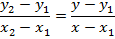
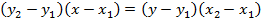
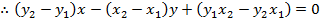
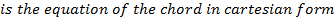
II.   IN PARAMETRIC FORM.

Consider the chord to an ellipse 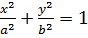 at the points. Hence the equation of the chord is given by

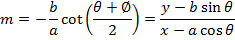
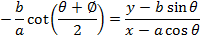
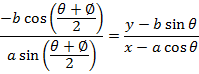
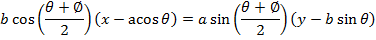
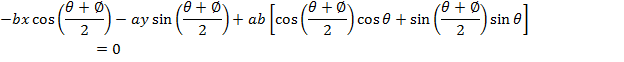
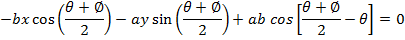
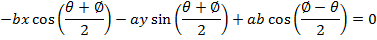
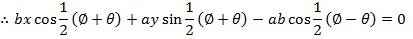
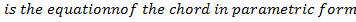
FOCAL CHORD OF AN ELLIPSE.

This is the chord passing through the focus of an ellipse

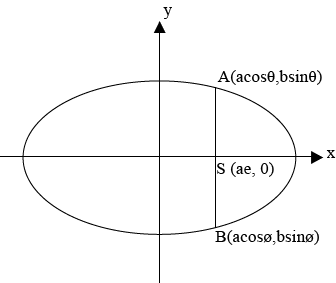
      Where 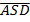 = is the focal chord
Consider the points A and B are respectively 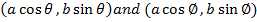 Hence
Gradient of AS = gradient of BS
Where s = (ae, o)

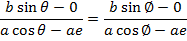
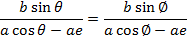
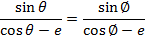
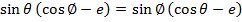
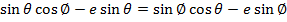
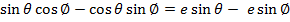
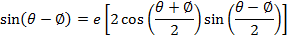
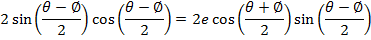
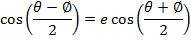
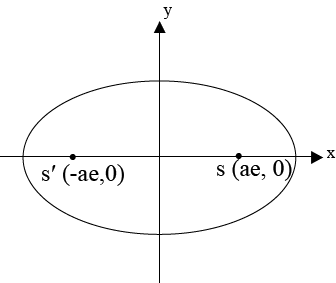
DISTANCE BETWEEN TWO FOCI.

Consider the ellipse below;

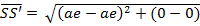                    ²

²

²

                                               

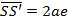
Where a = is the semi major axis

e = is the eccentricity

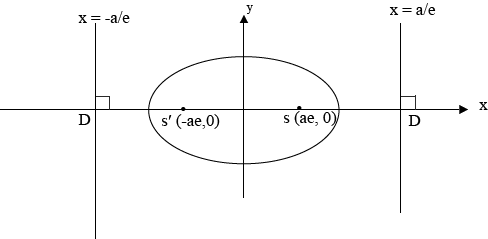
DISTANCE BETWEEN DIRECTRICES.

Consider the ellipse below

           

           

=

=

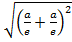
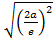
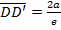
Where a – is the semi major axis
e – is the eccentricity

LENGTH OF LATUS RECTUM.

Consider the ellipse below

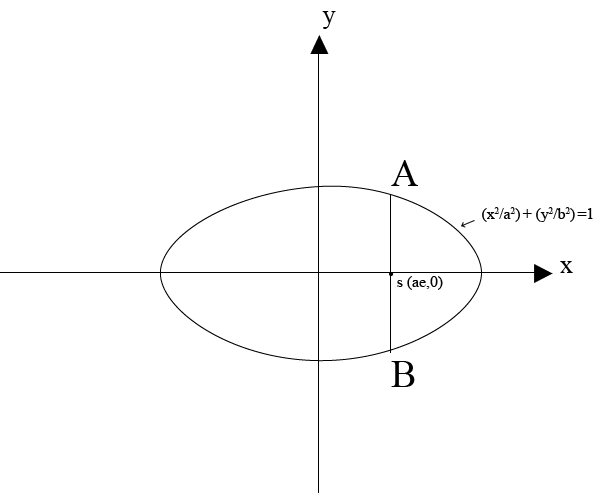
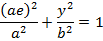
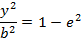
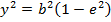
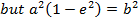
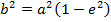
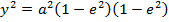
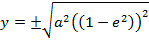
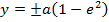
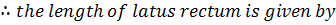
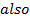
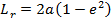
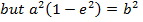
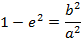
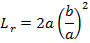
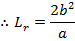
IMPORTANT RELATION OF AN ELLIPSE

Consider an ellipse  below

 

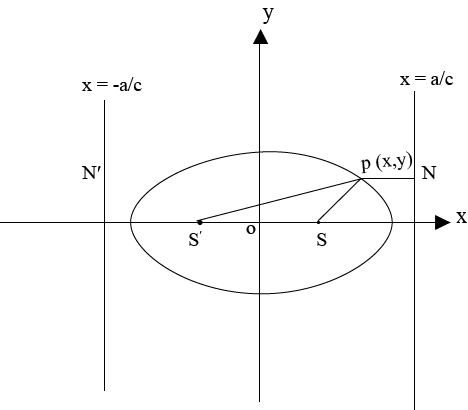
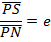
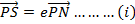
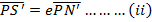
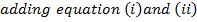
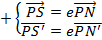
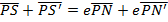
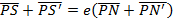
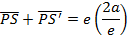
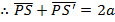
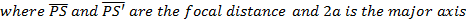
ECCENTRIC ANGLE OF ELLIPSE

.This is the angle introduced in the parametric equation of an ellipse
I.e
Where 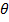     – is an eccentric angle
CIRCLES OF AN ELLIPSE
These are 1) Director Circle
2) Auxiliary circle

1.   DIRECTOR CIRCLE
– This is the locus of the points of intersection of the perpendicular tangents.

         

Consider the line 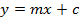 is tangent to the ellipse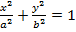
Hence

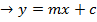
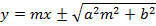
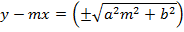
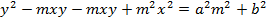
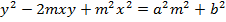
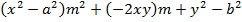
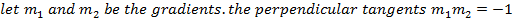
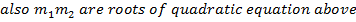
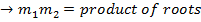
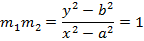
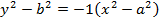
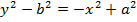
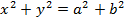
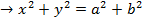
2.  AUXILIARY CIRCLE
– This is the circle whose radius is equal to semi – major axis

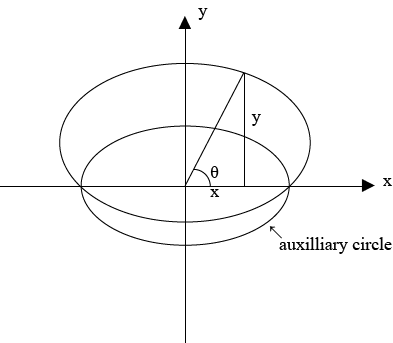
Using Pythagoras theorem

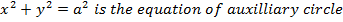
   a – is the radius of the auxiliary circle

CONCENTRIC ELLIPSE.

These are ellipse whose centre are the same.

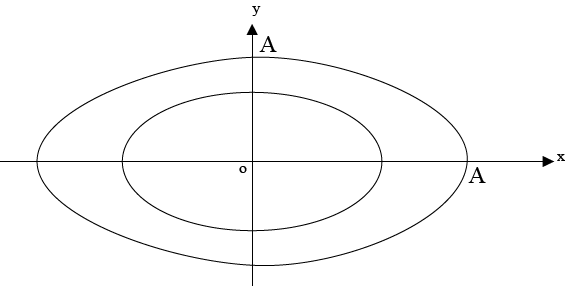
The equations of centric ellipse are;

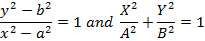
          Where  a and b semi – major and semi – minor axes of the small ellipse

A and B are the semi – major and semi – minor axes of the large ellipse

A – a = B – b

                         A – B = a – b·
Is the condition for concentric ellipse