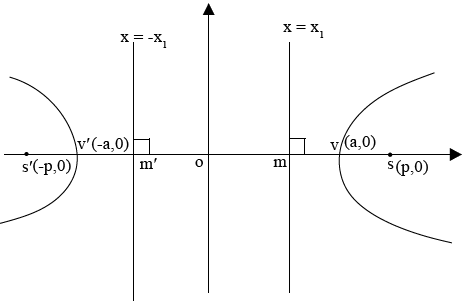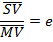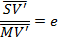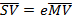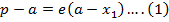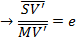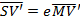ADVANCED MATHEMATICS FORM 6 – COORDINATE GEOMETRY II

TRANSLATED ELLIPSE

This is given by the equation

A. PROPERTIES

i) An ellipse lies along x – axis
ii) a > b
iii) Centre (h, k)
iv) Vertices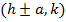
v) Eccentricity,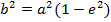
vi) Foci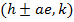
vii) Directrices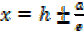
B. PROPERTIES
i) An ellipse has along y – axis
ii) b > a
iii) Centre (h, k)
iv) Vertices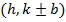
v) Eccentricity
vi) Foci

      Examples
 Show that the equation 4x² – 16x + 9y² + 18y – 11 = 0 represents an    ellipse and hence find i) centre ii) vertices iii) eccentricity iv) foci v) directrices.

          Solution

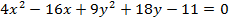
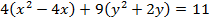
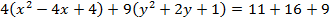
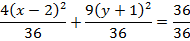
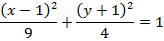
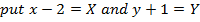
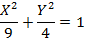
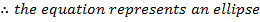
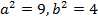
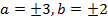
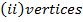
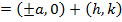
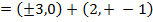
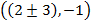
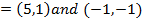
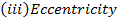
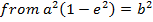
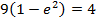
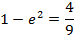
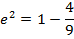
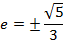
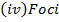
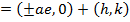
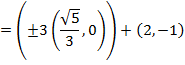
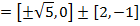
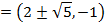
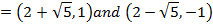
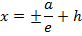
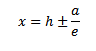
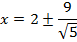
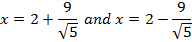
III.      HYPERBOLA

This is the conic section whose eccentricity ”e” is greater than one       ( e > 1)

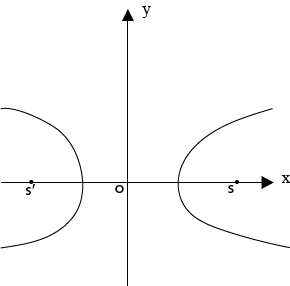
 The hyperbola has two foci and two directrices

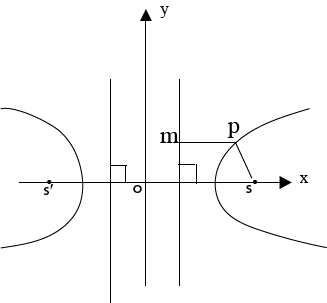
Where S and S’ are the foci of the hyperbola hence

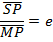
Where e > 1

EQUATION OF THE HYPERBOLA

There are;
i) Standard equation
   ii) General equation

1.    STANDARD EQUATION OF THE HYPERBOLA

          Consider