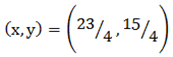PARALLEL AND PERPENDICULAR LINES
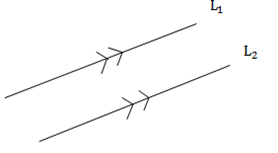
(a) PARALLEL LINES
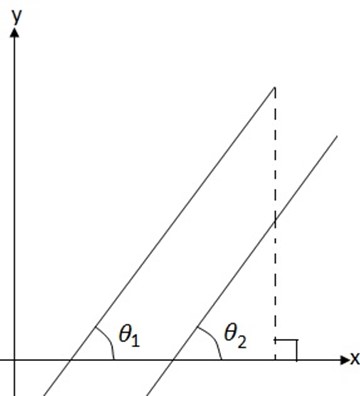
-Are the lines which never meet when they are produced
Means that 
is parallel to 
symbolically 
//
– -However condition for two or more lines to be parallel state that they posses the same gradient.
b) PERPENDICULAR LINES
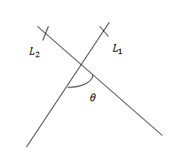
– -Are the lines which intersect at right angle when they are produced.
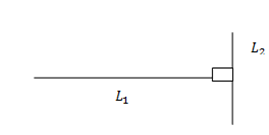
Means that 
is perpendicular to 
– -Symbolically is denoted as L1⊥L2
– -However the condition for two or more lines to be perpendicular states that “The product of their slopes should be equal to negative one”.
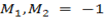
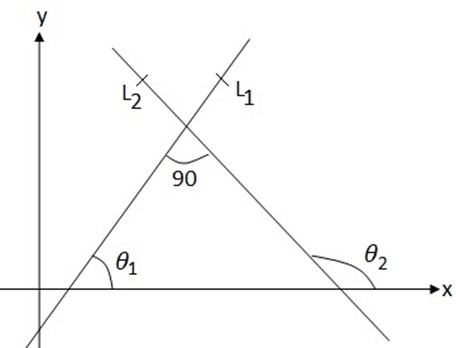
– -Let consider the figure below
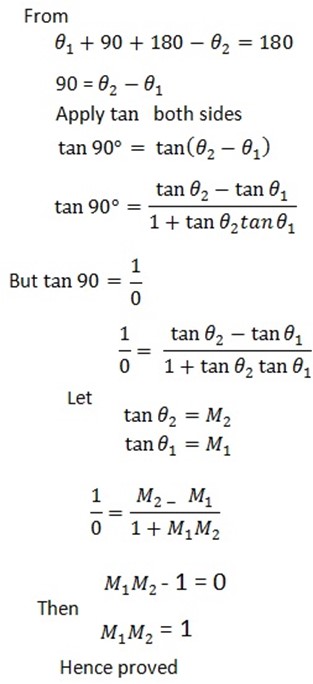
NOTE:
1. The equation of the line parallel to the line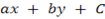 
= 0 passing through a certain point is of the form of 
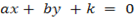. Where 
– is constant.
2. The equation of the line perpendicular to the line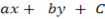 
pass through a certain point is of the form of 
when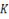 
– is constant.
3. The calculation of K above done by substitution certain point passing through.
THE EQUATION OF PERPENDICULAR BI SECTOR
– Let two point be A and B.
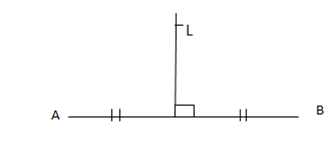
Where,
Line L is perpendicular bisector between point A and B.
Now our intention is to find the equation of L.
IMPORTANT STEPS
1. Determine the midpoint between point A and B.
2. Since L and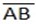 
are ⊥ to each other then find slope of L.
for
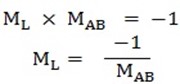
3. Get equation of L as equation of perpendicular bisector of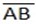 
by using 
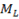and mid point of A and B.
THE COORDINATE OF THE FOOT OF PERPENDICULAR FROM THE POINT
THE POINT TO THE LINE
– -Our intention is to find the coordinate of the foot (x,y) which act as the point if intersection of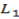 
and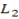 
.
– Let consider the figure below.
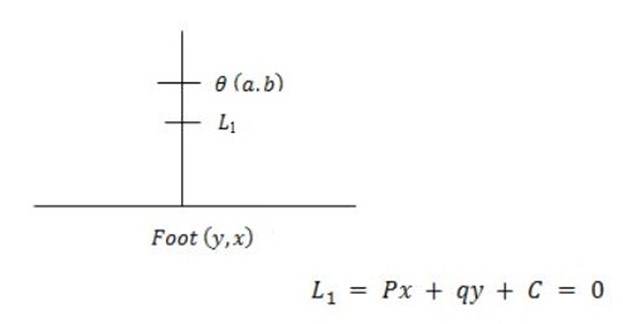
IMPORTANT STEPS
1. Get slope of formatted line i.e.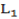 
and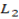 
then use if to get slope of L2. Since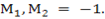 
2. From equation of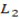 
by using 
and point provided from.
3. Get coordinate of the food by solving the equation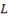 
and 
simultaneously as the way Y please.
EXAMPLE
1. Find the acute angle 6. between lines
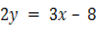and
2. Find the acute angle between the lines represented by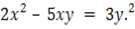 
3. find the equation of the line in which such that X – axis bisect the angle between the with line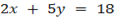 
4. find the equation of perpendicular bisector between A 
and B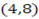 
5. Find the coordinate of the foot perpendicular from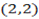 
of the line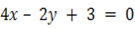 
6. Find the equation of the line parallel to the line 3x – 2y + 7 = 0 and passing through the point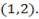 
7. find the equation if the line perpendicular to the line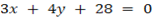 
and passing through the point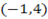 
8. Find the equation of perpendicular bisector of AB. where A and B are the point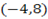 
and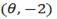 
respectively.
Solution
Given
Consider
From
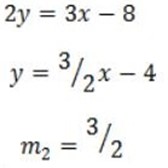
Also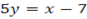 
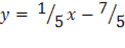
Recall
=
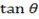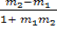
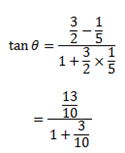
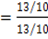
θ2tan-1 1
Therefore;
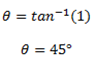
2)
Solution
Given
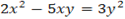
Factorize completely
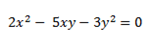
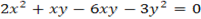
From
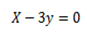
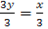
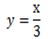
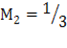
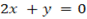
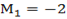
Recall
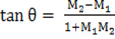
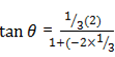
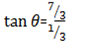
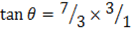
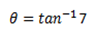
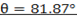
Given
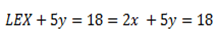
Consider the figure below
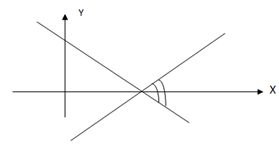
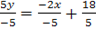
From
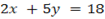
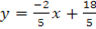
The slope is negative then at x –axis y=0
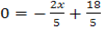
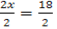
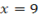
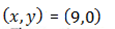
4) Solution
Given A 
B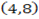 
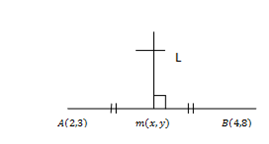
From
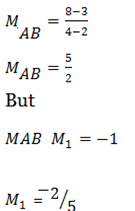
Also
Midpoint = 
M.p =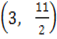 
Then
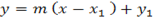
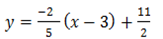
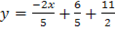
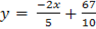
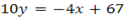
The equation is
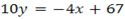
Solution
Given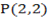 
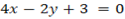
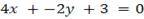
From
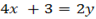
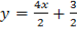
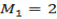
But
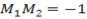
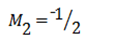
For the equation
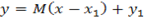
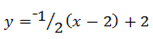
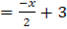
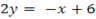
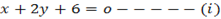
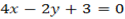
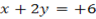
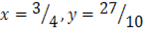
The coordinate of the foot is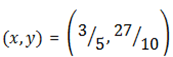 
The perpendicular line from point A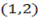 
to the straight line 
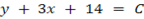intersect the line at point B. if the perpendicular is extended to C in such a way that AB = 
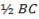. Determine line coordinate of C.
Solution
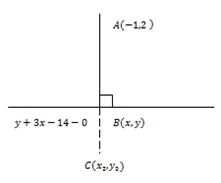
Given
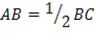
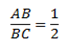
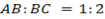
Let
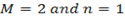
From
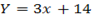
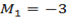
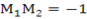
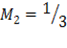
Then
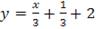
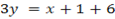
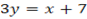
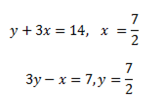
The coordinate of is 
since point B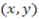 
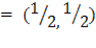
Recall
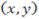
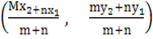
Since
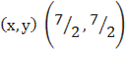
Then
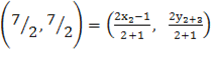
For x
Compare off
∴
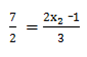
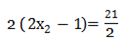
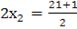
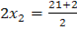
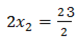
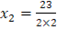
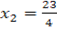
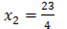
For y
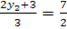
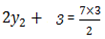
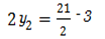
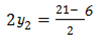
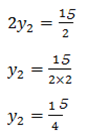
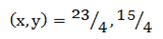
The coordinate of C is
