THE EQUATION OF ANGLE BISECTOR BETWEEN TWO LINES
* Consider the figure below.
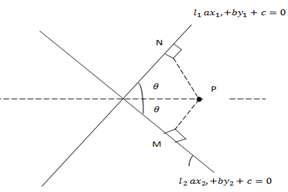
Where, PM and PN are perpendicular distance from point P. which are always equal.
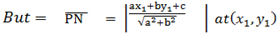
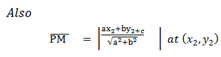
Since

Then
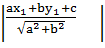 =
= 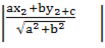
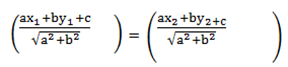
NOTE;
i) for the  equation take +ve
equation take +ve
i ii) for the  equation take –ve
equation take –ve
THE CONCURRENT LINES
These are the lines which intersect at the same point.
Example:
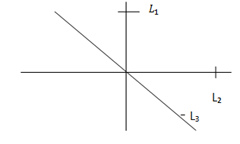
– where 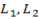 and
and 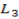 are concurrent line.
are concurrent line.
– However the point of intersection if concurrent line normally calculated under the following steps.
1. Select two equation of straight line which relate to each other from the those equation provided.
2. The get point of inter section of selected equation as usual. Points of intersection into the third equation in such a way that if the result of L.H.S is equal R.H.S imply that these line are currents lines.
Example;
i.Show that the lines 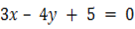
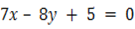 , and
, and 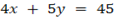 are current lines
are current lines
ii. Determine the value of M for which the lines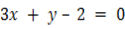 ,
, 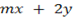 – 3 = 0 and
– 3 = 0 and 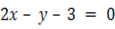 are current.
are current.
iii. Find the equation of bisect of angle formed by the lines represented by pair of the following.
a) 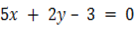 and
and 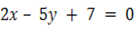
b) 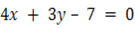 and
and 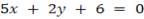
Solution:
1)Given
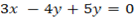
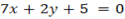
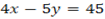
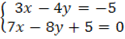
By solving since simultaneous equation
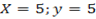
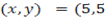 )
)
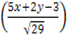 =
=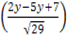
For the first equation take the it be cones
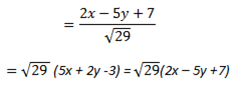
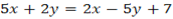
Then for the 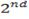 equation take cones from
equation take cones from
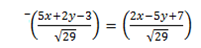
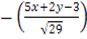 =
= 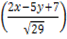
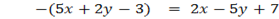
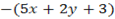 =
= 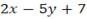
The equations of base equation of the angle are

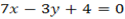
THE AREA OF TRIANGLE WITH THREE VERTICES
By geometrical method.
Consider the figure below.
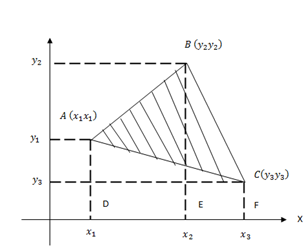
Our intention is to find the area of 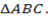
Now,
Area of  = area of trapezium ABED area of trapezium ACED
= area of trapezium ABED area of trapezium ACED
But area of trapezium 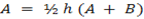
Also consider, Area of trapezium ABED

Area of trapezium DCEF
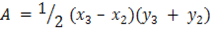
Area of trapezium
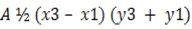
Then
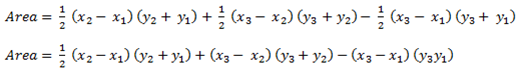
But simplification the formula becomes
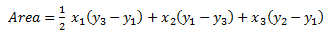
If ABC has A (x1, y1), B (x2, y2) and C (x3, y3) for immediately calculation of area the following technique should be applied by regarding three vertices of  as A (x1, y1), B (x2, y2) and C (x3, y3)
as A (x1, y1), B (x2, y2) and C (x3, y3)
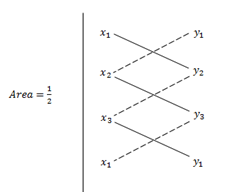
Area =