TRI – SECTION
-Is the process of dividing a certain line into three section or equal parts
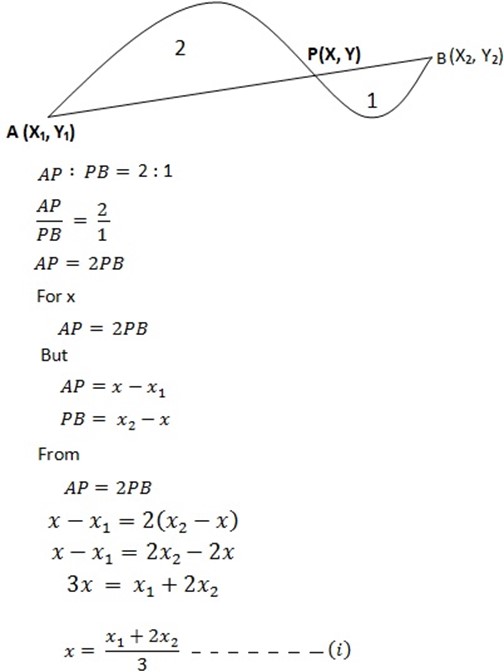
Where the coordinate P intersection depends on the two conditions.
i) When P is close to A
ii) When P is close to B
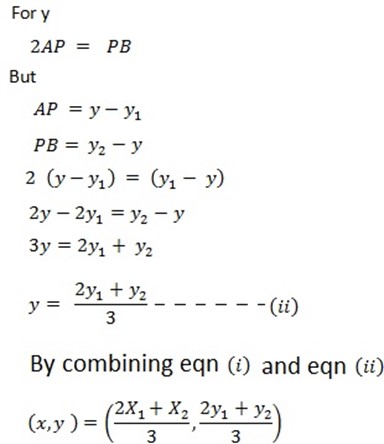
For P close to B.
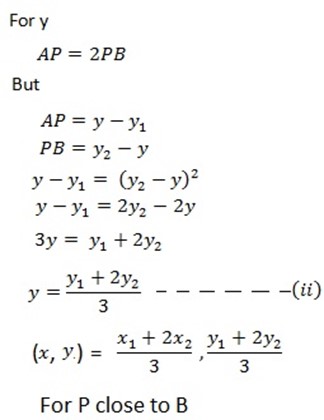
RATIO THEOREM
– -Is the theory based on a division of a lines segment either internally or externally.
1. INTERNALLY DIVISION
Is a division of a lines segment internally under the given condition of ratio.
-Let line AB being divided at R in ratio M: N.
Where
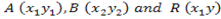
Ratio M: N.
-Consider the figure below.
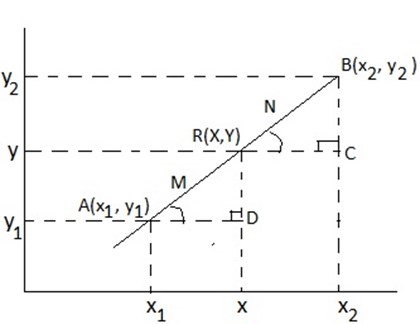
From similarities of ΔADR and ΔRCB.
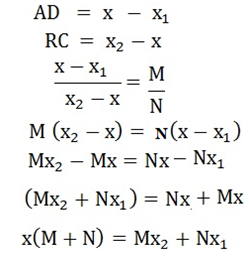
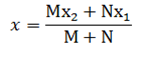
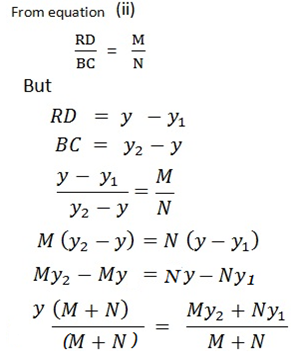
II. EXTERNALLY DIVISION
-Is the theory based on a division of a lines segment externally under the given ratio.
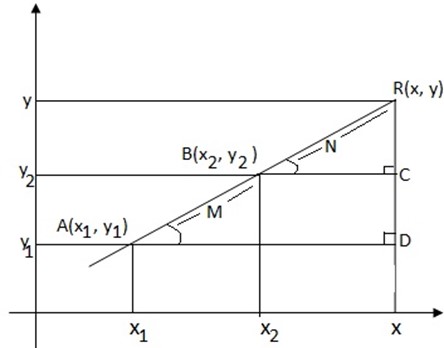
Let,
A (X1,Y1), B (X2,Y2) and R (X, Y) under ration R (X,Y).
-Consider the graph below.
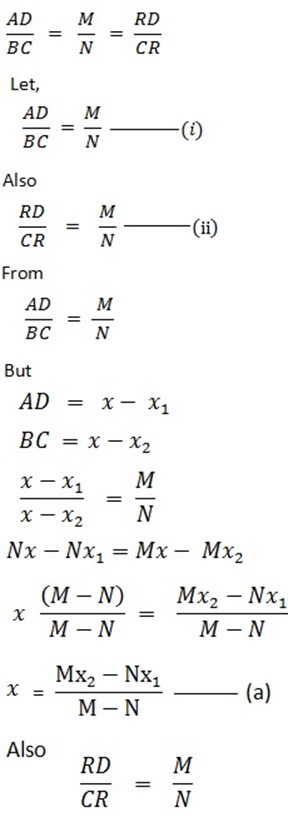
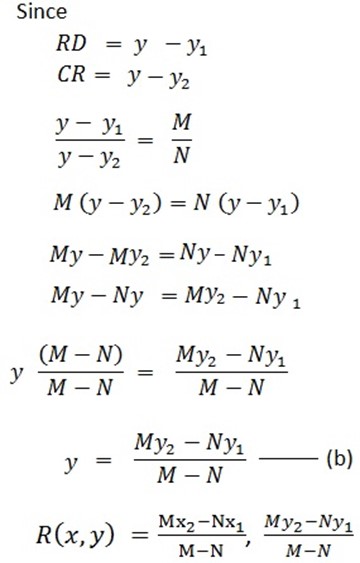
EXAMPLES
1. Find the coordinate of point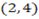 
and 
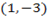divided internally or externally in the ration 
2. Find the point of in-section of a line a joining, point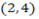 
and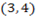 
if P is closed of A.
3. Find the coordinate of in – section of a line AB at point P. If B is closer to A given that A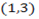
and B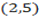
SOLUTIONS
1. For internally division
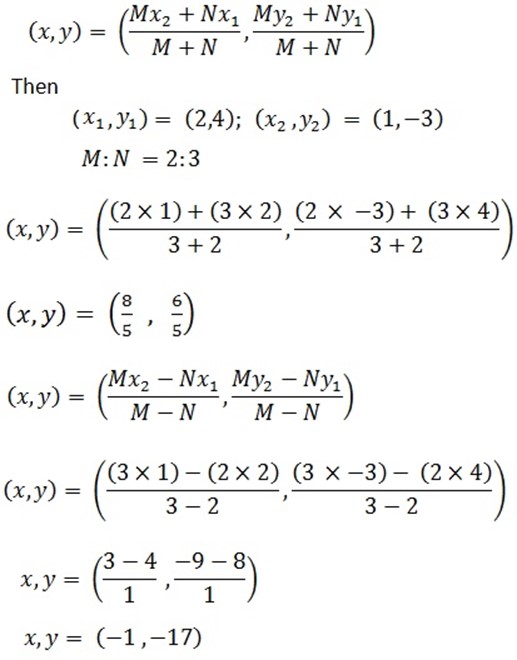
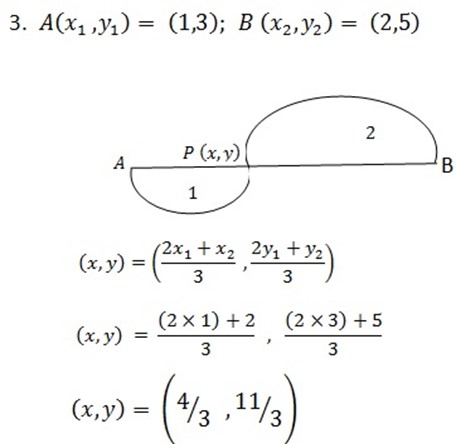
GRADIENT
– Is the ration expressed as vertical change over horizontal change.
OR
– Is the ratio between change in Y over change in X.
Mathematically
gradient denoted as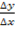 
i.e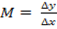 
However the gradient can explained by using three different methods.
i) . GRADIENT FROM ANGLE OF INCLINATION
ii). GRADIENT FROM THE CURVE (calculus method)
iii). GRADIENT BETWEEN TWO POINTS.
– Consider the figure below.
GRADIENT FROM ANGLE OF INCLINATION
-Let θ be angle of inclination
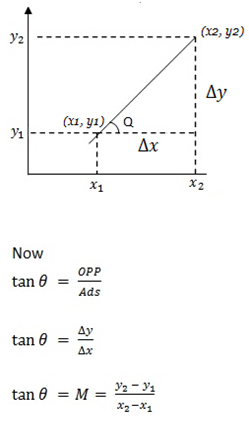
GRADIENT FROM THE CURVE
This is explained by using calculus notation idea where;
of a curve at a given point.
However gradient can be obtained directly from the equation of a straight line as coefficient of x from the equation in form of
y =mx + c