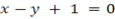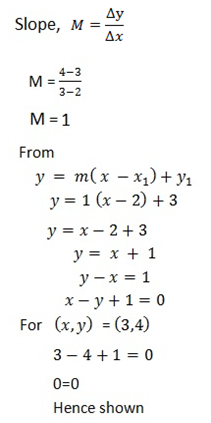BEHAVIOUR OF GRADIENT BETWEEN TWO POINT
-Lets two points be  which can be used to form the line AB.
which can be used to form the line AB.
(i) If 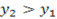 , and
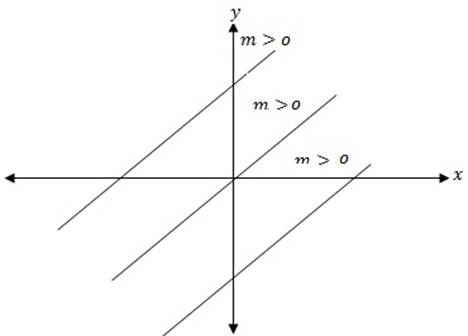
, and  the line increase from left to right imply positive slope.
the line increase from left to right imply positive slope.
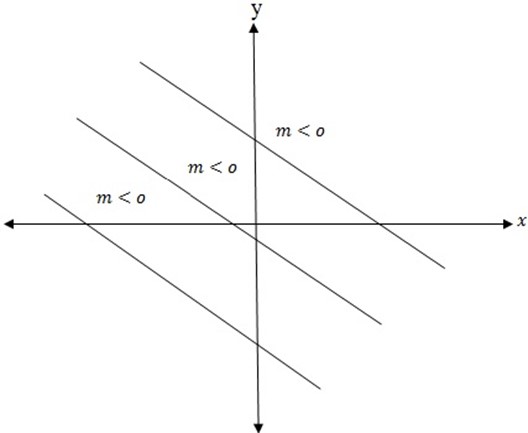
(ii) If  the line decrease from right to left imply
the line decrease from right to left imply  slope.
slope.
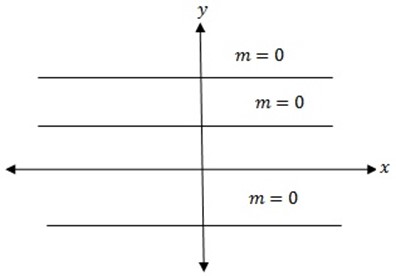
(iii) If  the line is horizontally with zero gradient
the line is horizontally with zero gradient
(iv) If 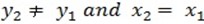 the line is vertical with infinity gradient
the line is vertical with infinity gradient
COLLINEAR POINTS
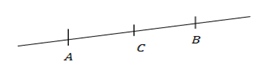
– – Are point which lie on the same straight line
Where,
A, B, and C are collinear.
– – The condition of collinear points have the same slope/ gradient
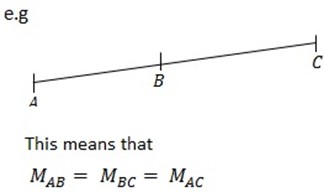
Note:
If A (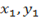 ); B
); B 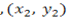 and C
and C 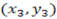 are collinear then the area of
are collinear then the area of 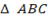 = 0.
= 0.
Example 1
1. 1.Determine the value of K such that following points are collinear:-
a) 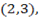
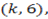 and
and 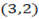
b) 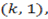
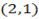 and
and 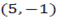
2. Show that the points 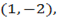
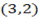 , and
, and 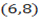 are collinear.
are collinear.
3. The straight line 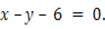 Cut the curve
Cut the curve 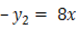 at P and Q. Calculate the length PQ.
at P and Q. Calculate the length PQ.
4. If A and B are products of OX and OY respectively. Show that xy=16. If the area of  is 8 units square.
is 8 units square.
Solution:
A  B
B , C
, C 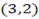
For collinear point
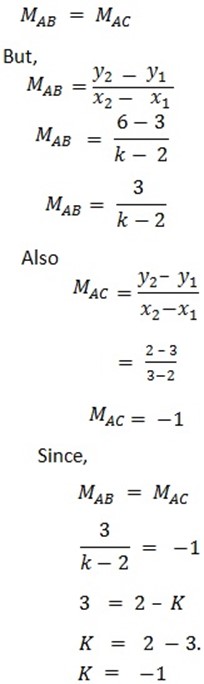
2. Give
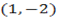 ; B
; B 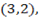 C
C 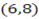

Alternatively
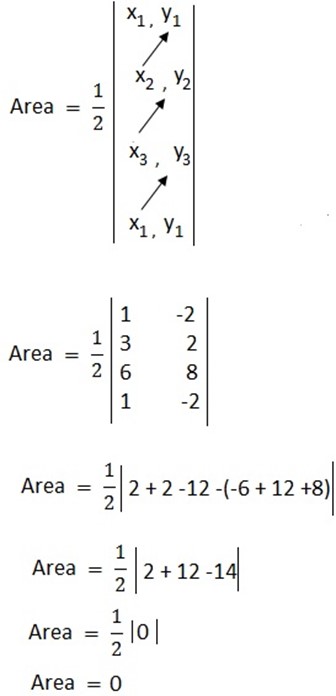
Since the area of ΔABC is 0 unit hence the points are collinear.
3. Given
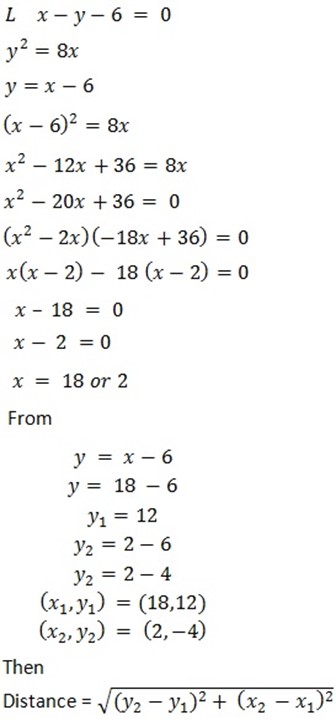

4. Given
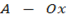
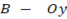
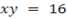
Since
Area of ΔOAB = 8 square units
Then,

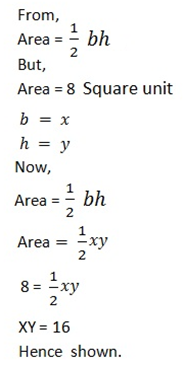
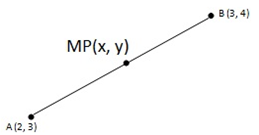
5. If  and
and 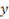 are the collinear of midpoint of the line forming the points
are the collinear of midpoint of the line forming the points 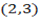 and
and 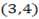 show that, x-y+1=0.
show that, x-y+1=0.
Solution
M.P = (x, y)
A 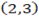 and B
and B 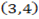
Required