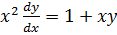First order homogenous D.E
In first order H.D.E all the terms are of the same dimension
Consider the table about dimensions
| Term | X | x2 | 1/x | xn | 3 | y | yn | x2/y | x2y |
| Dimension | 1 | 2 | -1 | n | O | 1 | N | 1 | 3 |
|
|
dy/dx | dy2/dx2 | xdy/dx | yx | |||||
| 0 | 1 | 2 | |||||||
edu.uptymez.com
O shows there is no effect on the term
Which of the following equation are first order homogeneous
a) x2 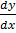 = y2
= y2
b) xy 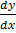 = x2 + y2
= x2 + y2
c) x2
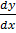 = 1 + xy
= 1 + xy
d) (x2
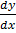 =
= 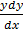
e) (x2 – y2) 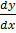 = 2xy
= 2xy
f) (1 + y2) 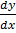 = x
= x
Solution of 1st order Homogeneous differential equation
1st order homogeneous d.e can be written in the form  = Q
= Q
Where both P and Q are function of and have same dimension.
Suppose p and Q hence the dimension
Then divide by xn and use the substitution
Y = vx = v = 
i.e 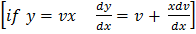
Example 1.
Solve 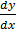 =
= 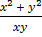
Solution
Since all terms are of degree 2, i.e the equation is homogeneous
Let y = vx
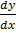 = v +
= v + 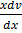
And
 =
= 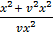
= 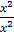 (
( )
)
= 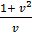
V + 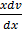 =
= 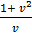
 =
= 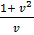 – v
– v
= 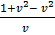
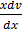 =
= 
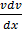 =
= 
 =
=  dx
dx
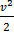 = lnx + c
= lnx + c
But v = 
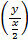 2 = ln x + c
2 = ln x + c
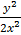 = lnx + c
= lnx + c
Y2 = 2x2 (lnx + c)
Example 2
Solve xy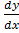 = x2 + y2
= x2 + y2
Solution
All terms are of the order 2
xy 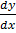 = x2 + y2……
= x2 + y2……
Let y = vx
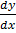 = v +
= v + 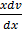
From the equation…
 =
= 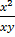 +
+ 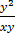
But y = vx
= 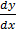 =
= 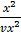 +
+ 
= x2
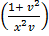
= 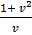
V + 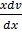 =
= 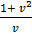
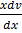 =
= 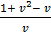
= 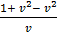
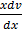 =
= 
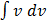 =
= 
 = lnx + A
= lnx + A
But v = 
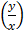 2 = lnx + A
2 = lnx + A
Y2 = 2x2 (lnx + A)
Example 3
Solve the following
(x2 + xy) 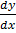 = xy – y2
= xy – y2
Solution
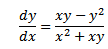
Let y = vx
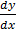 = v +
= v + 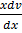
And
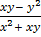 =
= 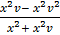
= 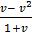
v + 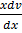 =
= 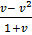
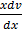 =
=  -v
-v
= 
=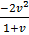
 =
= 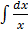
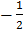 [(
[(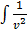 dv +
dv + 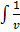 dv)] =
dv)] = 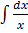
–½ (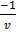 + ln v) = lnx + c
+ ln v) = lnx + c
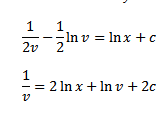
 = ln (x2 V) + 2c
= ln (x2 V) + 2c
But v = 
 = ln (x2
= ln (x2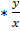 ) + 2c
) + 2c
 – 2c = ln (x2.
– 2c = ln (x2. )
)
Let ln A = -2c
 + ln A = ln xy
+ ln A = ln xy
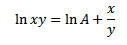
Xy = Aex/y
EXERCISE
Solve the differential equation
1. x2 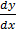 = y (x + y)
= y (x + y)
2. (x2 + y2) 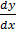 = xy
= xy
First order exact differential equation
We know that 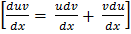
Now consider
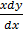 + y = ex
+ y = ex
Integrating both side w.r.t.x
= xy = e2 + c
Y =  (ex + c)
(ex + c)
Y =  (ex + C)
(ex + C)
2. Find the general solution of the following exact differential equation.
i)exy + ex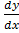 = 2
= 2
ii) cos x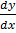 – ysin x = x2
– ysin x = x2
Solution
i) Given
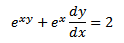
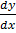 (exy) = 2
(exy) = 2
Integrating both sides with respect to x
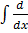 (exy) dx =
(exy) dx = 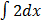
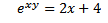
ii) Given
cosx 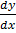 – y sin x = x2
– y sin x = x2
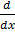 (y cos x) = x2
(y cos x) = x2
Integrating both side with respect to x
= 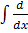 (exy) dx =
(exy) dx = 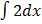
Y cos x = 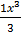 + c
+ c
3ycosx = x3 + 3C
3ycosx = x3 + 4
3. 
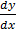 + lny = x + 1
+ lny = x + 1
Soln
Given 
 + lny = x + 1
+ lny = x + 1
Integrating both sides w.r.t x
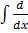 (x ln y) dx =
(x ln y) dx = 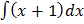
Xln y = ½ x2 + x + C
2xlny + x2 + 2x + 2c
2x lny + x2 + x + A
Integrating factors
Consider first order differential equation of the form
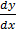 + py =Q
+ py =Q
Where p and Q are functions of x
Multiplying by integrating factor F both sides will make an exact equation
i.e F 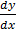 + Fpy + FQ…….i
+ Fpy + FQ…….i
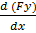 =
= 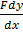 +
+ 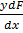
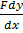 +
+ 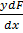 …..ii
…..ii
Comparing (i) (ii)
 + Fpy =
+ Fpy = 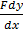 +
+ 
Fpy = 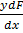
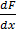 = Fp
= Fp
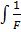 dF =
dF = 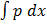 by separating of variables
by separating of variables
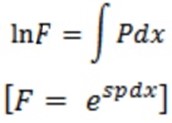
F =  is the required integrating factor
is the required integrating factor
Examples
1. Solve 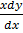 + y = x3
+ y = x3
Solution
 + y = x3
+ y = x3
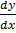 +
+  = x2
= x2
Compare with 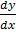 + py = Q
+ py = Q
P = 
Then 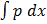 =
= 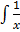 dx
dx
= ln x
If F = eln x
F = eln x
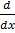 (xy) = x2 x
(xy) = x2 x
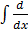 (xy) =
(xy) = 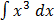
Xy =  x4 + C
x4 + C
2. Solve
(x + 1) 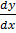 + y + (x + 1)2
+ y + (x + 1)2
Soln
(x + 1) 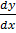 + y + (x + 1)2
+ y + (x + 1)2
= 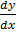 +
+ 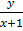 = x + 1
= x + 1
= 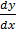 +
+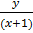 , y = x + 1
, y = x + 1
P = 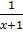
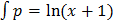
F = esp
= eln (x + 1)
= x + 1
Y (x + 1) = 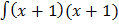
= 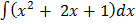
=  x3 + x2 + x + c
x3 + x2 + x + c
= 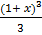 + c
+ c
Y = 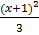 +
+ 
3. Solve (1 – x2) 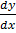 – xy = 1
– xy = 1
Solution 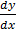 –
– 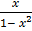 y =
y = 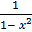
P = 
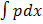 =
= 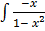 dx
dx
= ½ ln (1 – 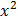 )
)
F = e ln (1 – 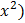 ½
½
= (1 – x2) ½
Y  =
= 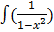
 dx
dx
= 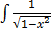 dx
dx
Y = 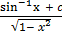
4. tanx 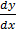 + y = ex tan x
+ y = ex tan x
Solution
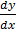 +
+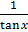 , y = ex
, y = ex
P = 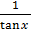 = cot x
= cot x
 =
= 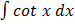
= ln 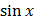
F = eln 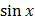
=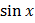
Y 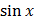 =
= 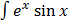 dx
dx
Integrating by parts the R.H.S
=  = ex
= ex
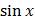 –
– 
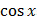 dx
dx
= ex sin x – (ex cos x + 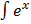
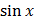 dx
dx
= ex
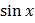 – ex
– ex
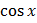 –
– 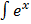
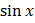 dx
dx
2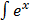 sin x dx = e x (
sin x dx = e x (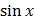 –
–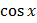 )
)
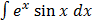 =
= 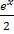 (
(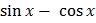 )
)
Y sin x = 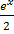 (
(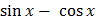 ) + c
) + c
Bernoulli’s equation
This is a first order D.E of the form
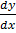 + p (x) y = Q (x) y n
+ p (x) y = Q (x) y n
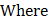 p (x) and Q (x) are functions of x or constant
p (x) and Q (x) are functions of x or constant
Steps
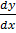 + p (x) y = Q (x) yn……i
+ p (x) y = Q (x) yn……i
Divide both sides by yn gives
Y-n 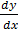 + p (x) y1 – n = Q (x)…… (ii)
+ p (x) y1 – n = Q (x)…… (ii)
Let z = y1-n
(1 – n) y-n 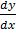
Multiplying (ii) by (1 – n) both sides gives
(1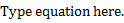 – n) y-n
– n) y-n 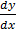 + (1 – n) p (x) y (1 – n) = (1 – n) Q (x)
+ (1 – n) p (x) y (1 – n) = (1 – n) Q (x)
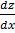 + (1 – n) p (x) y (1 – n) = (1 – n) Q (x)
+ (1 – n) p (x) y (1 – n) = (1 – n) Q (x)
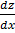 + p1 (x) y (1 – n) = Q1 (x)
+ p1 (x) y (1 – n) = Q1 (x)
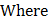 p1 (x) and Q1 (x) are functions of x or constant
p1 (x) and Q1 (x) are functions of x or constant
But z = y (1 -n)
= 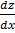 + p1 (x) z = Q1 (x)……..ii
+ p1 (x) z = Q1 (x)……..ii
iii) is linear the use of integrating factor can be used
Example 1
Solve  +
+ 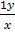 = xy2
= xy2
Solution
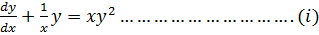
Dividing both sides by  gives
gives
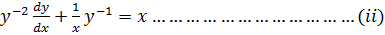
Let Z = 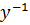
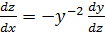
Multiply (ii) by -1 gives
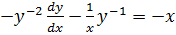
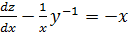
But Z = 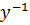
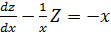
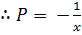
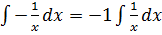
= 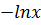
= 
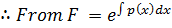
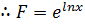
= 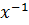
Then Z.F= 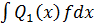

= -1
= 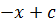
But Z = 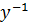

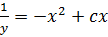
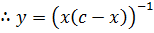
Example 2
Solve 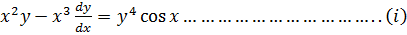
Solution
1st Expressing the equation in the form

– 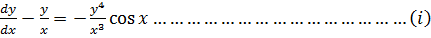
– 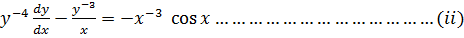
Let Z = 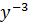
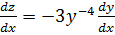
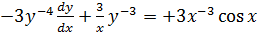
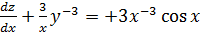
But Z = 
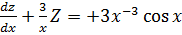
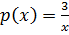

= 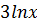
= 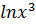
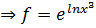
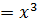
Then
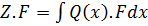
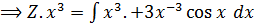
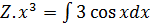
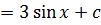
But Z = 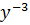
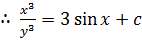
Example 3
Solve 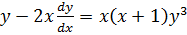
Solution
Expressing the equation in the form
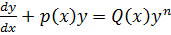
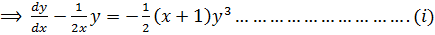
Then dividing by 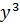
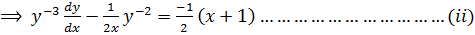
let Z = 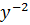
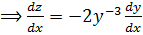
Multiply (ii) by -2 gives
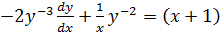
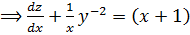
But Z = 
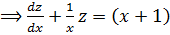
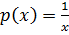
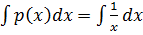
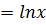
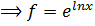

Then, 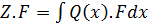
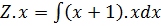
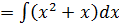
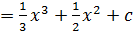
But Z = 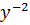
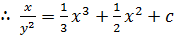
Exercise
Solve the following first order D.es
1. 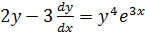
2.