ADVANCED MATHEMATICS FORM 6 – DIFFERENTIAL EQUATION

Second order Differential Equations

Second order differential equation is of the form of;

 

Where a, b, c are constant coefficients and 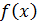is a given function of x

If   the equation is homogeneous otherwise it is a non-homogeneous

Which of the following are linear H.D.Es

1.    

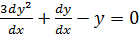
2.    

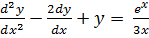
3.    

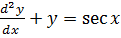
4.    

5.    

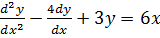
Characteristic (Auxiliary) Equation for H.DE

Consider a linear non-homogeneous 2^nd order D.E

 

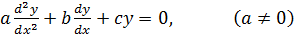
Let y = u and y=v be two solution of the equation 

Where u and v a functions of x

 

 

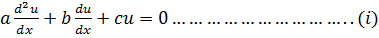
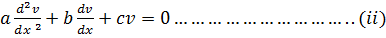
Adding (i)  & (ii) gives

 

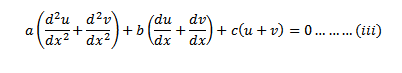
Then,

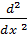
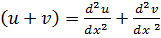  and

 

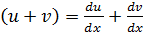
Becomes

   

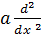
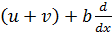
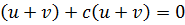
If y = u and y = v are the solutions of the equation

 

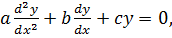
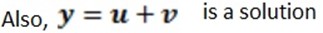
 Suppose a = 0

 

i.e.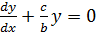   

 

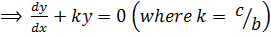
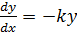      (separable)

 

 

 

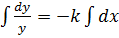
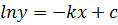
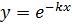 (where 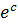is constant)

Take m for –k

–         is the solution of dy +ky

Also will be the solution of the equation

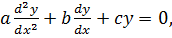 if it satisfies the equation

If

    

 

 

 

 

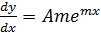
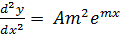
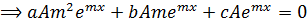
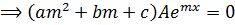
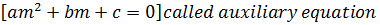
The values will be 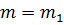 and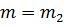

If 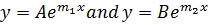  are two solution

 

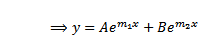
Note that: 
If the Auxiliary equation has

(i)   Two real roots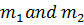  
     
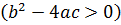
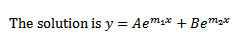
(ii)    Equal roots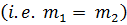
        
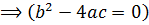
      The solution is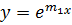  

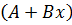
(iii)  2 Complex roots to the auxiliary equation
        
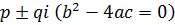
     The solution is

Examples

Solve the following 2^nd order Des

1.    

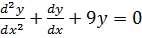
Solution

Auxiliary equation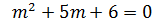

 

 

 

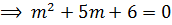
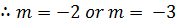
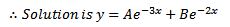
2.    

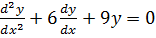
Solution

The auxiliary equation is

 

 

 

 

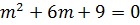
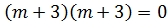
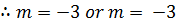
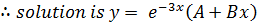
3.    

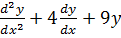
      Solution

Auxiliary equation is

 

 

 

 

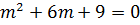
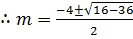
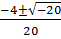
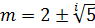
In this case P=-2 and q =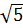

 

Exercise

Solve the following

1.      
 
2.      
 
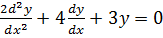
3.    
 

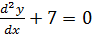
Non homogeneous 2^nd order D.E

Consider the equation

 

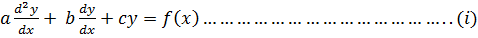
If 

 

 

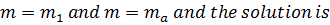
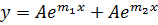
The general solution of (i) is given by

 Note that

 is called complementary function matas R.H.S Zero

Y = f (x) is called particular intergral makes R.H.S 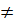0

Consider the R.H.S function

i.e if 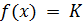         assume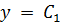  

                                 

        

         

      

      

 Examples

1.     Solve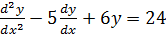  

Solution

C.F solve L.H.S = 0

 

 

 

 

 

 

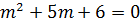
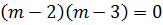
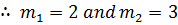
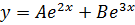
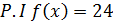
Assume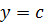

             

           

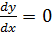
Substituting in the given equation gives

 

 

 

 

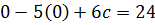
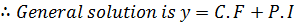
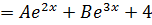
2.     Solve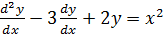  

Solution

(i)   C.F: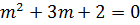  

       

          

        

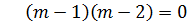
(ii)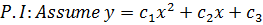     

 

 

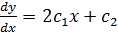
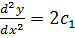
Substituting into the given equation

 

 

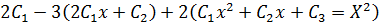
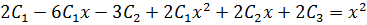
Collecting like terms

 

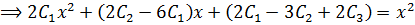
Comparing L.H.S to R.H.s

 

 

 

 

 

 

 

 

 

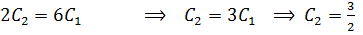
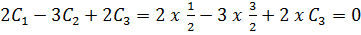
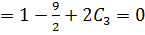
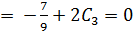
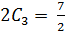
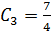
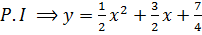
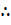  General solution

 

3.     Solve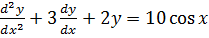   

Given that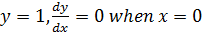

Solution

C.F: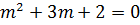 

        

        

        

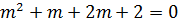
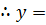
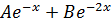
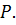I: Assume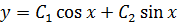

 

 

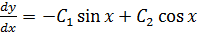
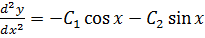
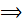
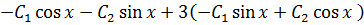  +2 

 

 

 

 

 

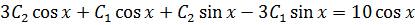
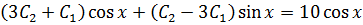
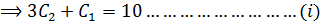
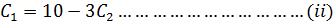
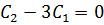
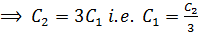
Substitute into (i)

 

 

 

 

 

 

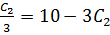
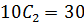
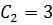
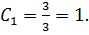
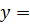
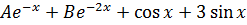
But y = 1,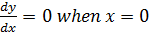

1= A + B + 1

A + B = 0

 

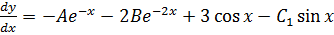
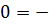A-2B+3

………………………….(i)

 

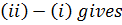
B = 3

Substituting into (ii) gives

A + 3 = 0

A = -3

 

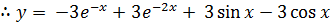
4.     Solve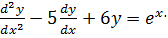

Solution

           C.F: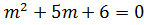
 
             
            
             
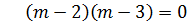
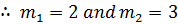
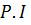
Let y =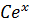  

 

 

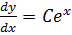
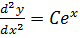
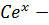5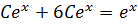 

2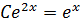 

2C=1

 

 

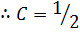
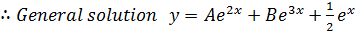
Note that: if P.I is contained in the C.F multiply the assumed P.I by x and go on

Example

Solve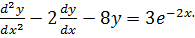

Solution

C.F: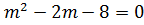 

 

 

 

 

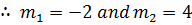
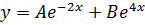
P.I: Assume y =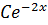

Since 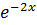 is already contained

 

 

 

        

        

 

 

 

 

 

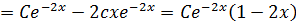
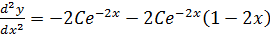
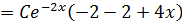
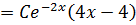
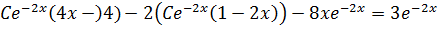
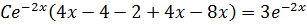
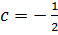
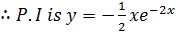
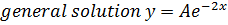 +B 

 Exercise

Solve the following

(i)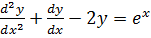    

2^nd order equations which are reducible to 1^st order
Consider 2^nd order equation which can not be written in the form
 
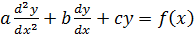
i.e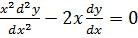   
Such equation will be solved by the substitution of: –

 

 

 

 

 

 

 

 

 

 

 

 

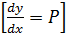
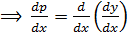
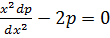
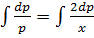
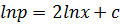
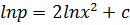
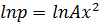
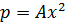
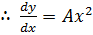
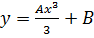
Where A and B are constants
Example
Solve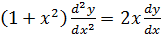
Solution
Let
 
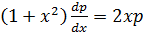
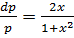 dx
 
 
 
 
 
 
 
 

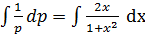
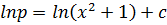
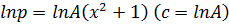
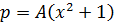
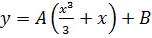
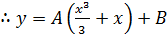
Example

Solve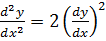  

Solution

Let p =

 

 

 

 

 

 

 

 

 

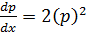
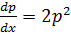
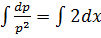
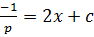
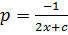
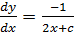
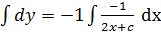
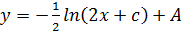
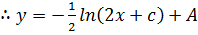
Example

 

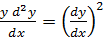
Solution

Let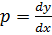 

    

   

    

 
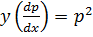
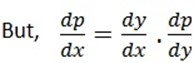
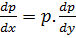
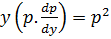
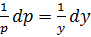
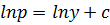
In p= ln Ay where c= ln A
P = Ay

i.e.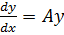

 

 

 

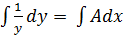
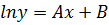
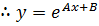
Note that:

      – If  P.I is contained in C.F, and C.F is of real  roots Assume 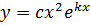 if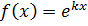

      – If  C.F is a distinct root, but one root is the  same as that on P.I, assume 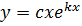if

      – If 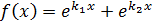 , assume  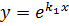independently followed by  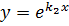then add to obtained a P.I