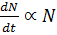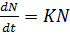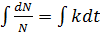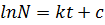Applications of differential Equations
1. i. Population growth
The rate of population growth id differently proportional to the number of inhabitants present at specific time.
If N is the number of inhabitants at specific time.
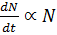
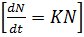
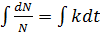
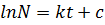
When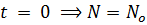 
i.e.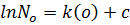 
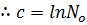
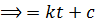
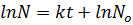
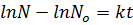
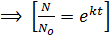growth equation
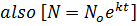
If the population of a certain place doubles in 50 years. After how many years will the population treble and the assumption that the rate of increase is proportional to the number of inhabitant in the place.
Solution
Let N be the number of inhabitants at time t.
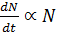
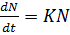
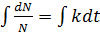
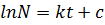
When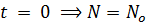 
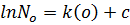
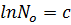
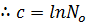
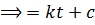
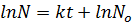………………………..(i)
When t = 50 years, N=2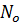
=
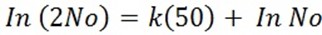
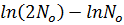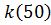
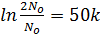
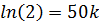
K =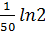 
Substituting into (i)
ln N = kt +ln No
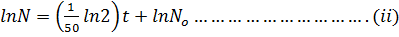
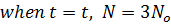
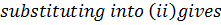
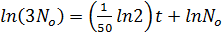
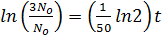
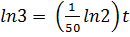
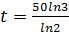
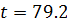
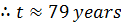
Example
The population of Kenya is known to increase to a rate proportional to the number of people living there at any given time. In 1986 the population was 1.1 times that of 1984 and 1987 the population was 18,000,000. What was the population in 1984?
Solution
Let N be the number of people at time, t
