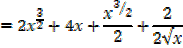DERIVATIVES
Slope of a curve
A curve has different slopes at each point. Let A, B, and C be different points of a curve f (x)

Where ðx is the small increase in x
ðy is the small increase in y
The slope of chord AC =
If C moves right up to A the chord AC becomes the tangent to the curve at A and the slope at A is the limiting value of 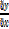

Therefore
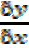 =
= 
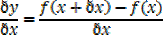
The gradient at A is
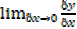 =
=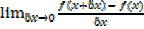

or
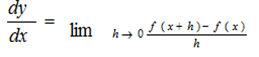
This is known as differentiating by first principle
From the first principle
i) f(x)= x
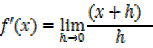
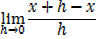
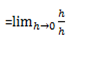
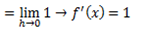
ii) f(x)= x2
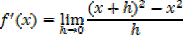
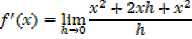
= 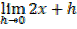
∴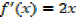
iii) f(x) =x3
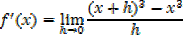
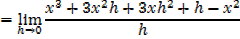
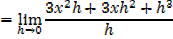
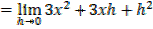
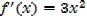
iv) f(x)= xn
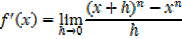
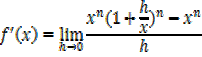
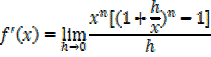
By binomial series
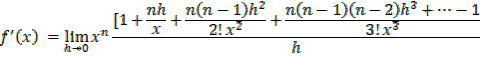
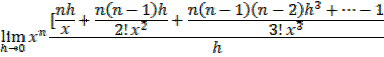
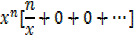
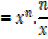
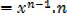
In general
If 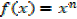
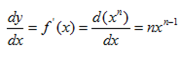
Example
Differentiate the following with respect to x
i)y = x2+3x
Solution
y =x2+3x
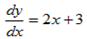
ii) 2x4+5
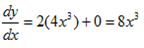
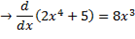
iii)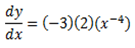
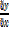 =
=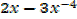
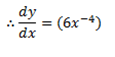
Differentiation of products functions [ product rule]
Let y =uv
Where u and v are functions of x
If x → x+ðx
u → u +ðu
v → v+ðv
y → ðy +y
y= uv ……i)
Therefore
y+ðy = [ u+ðu][v+ðv]
y+ðy = uv +uðv+vðu +ðuðv….ii
Subtract (i) from (ii)
δy =uðv +vðu +ðuðv
Therefore
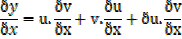
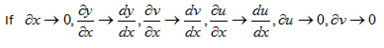
Therefore

Therefore
If y= uv
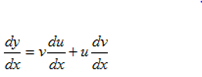 It is the product rule
It is the product rule
Examples
Differentiate the following with respect to x
i) y = [ x2+3x] [4x+3]
ii) y = [ 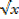 +2] [x2+2]
+2] [x2+2]
Solution
Y = [x2+3x] [4x+3]
Let u = x2+3x
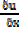 = 2x+3
= 2x+3
V = 4x+3
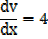
Therefore

=4x2+12x+8x2+12x+6x+9
=12x2+30x+9
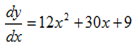
ii)Let u = 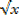 +2
+2 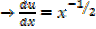 →
→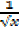
v = x2+2 
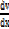 =2x
=2x
Therefore