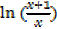ADVANCED MATHEMATICS FORM 5 – DIFFERENTIATION

DIFFERENTIATION OF A QUOTIENT [QUOTIENT RULE]

Let y =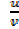 where u and v are functions of x

          

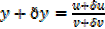
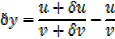
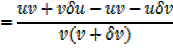
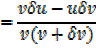
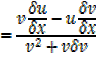
As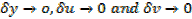

Exercise

Differentiate the following with respect to x

                                I.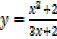   

                             II.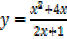    

DIFFERENTIATION  OF A FUNCTION [CHAIN RULE]

If y = f(u), where u = f(x)

Then

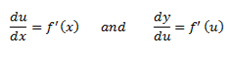
Therefore

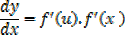
PARAMETRIC EQUATIONS

Let y = f(t) , and x = g (t)

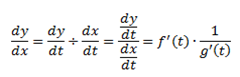
Example

        I.            Find 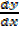 if y = at² and x = 2at

Solution

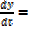2at

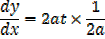
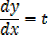
IMPLICIT  FUNCTION

Implicit function is the one which is neither x nor y a subject e.g.

1)     x²+y² = 25

2)     x²+y²+2xy=5

One thing to remember is that y is the function of x

Then

1.               

           

            

            

             

            ∴    

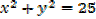
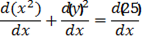
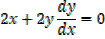
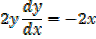
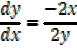
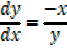
2.     x² +y² + 2xy = 5

   

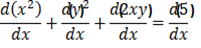
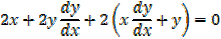
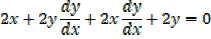
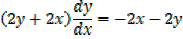
Exercise

Find 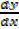when x³ + y³ – 3xy² = 8

Differentiation of trigonometric functions

1)     Let y = sin x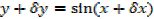….. i

…(ii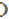

,

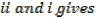
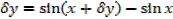
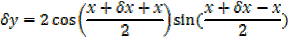
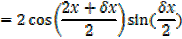
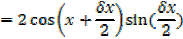
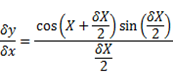
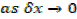
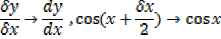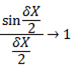
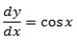
Provided that x is measured in radian [small angle]

2. Let y = cos x …… (i)

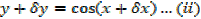
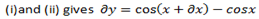
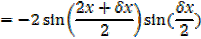
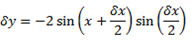
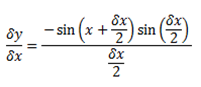
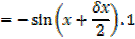
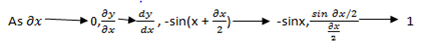
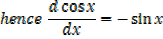
3.      Let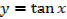

 

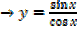
From the quotient rule

 

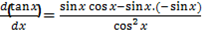
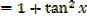
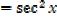
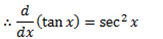
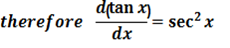
4.      Let y = cot x

              

∴

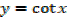
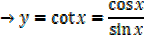
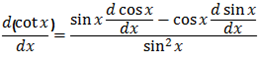
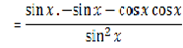
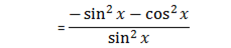
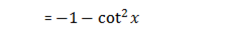
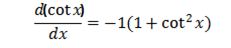
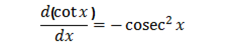
5.      y =

      

∴

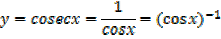
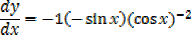
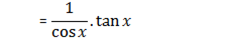
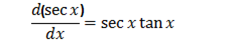
Let y =cosec x

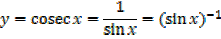
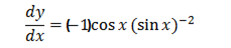
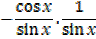
Therefore          

Differentiation of inverses

1)     Let y = sin^-1x

      x = sin y

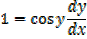
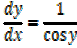
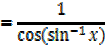
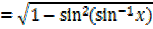
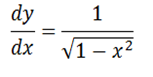
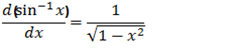
2)     Let y = cos^-1 x

        x= cos y

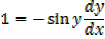
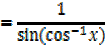
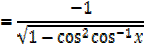
3)     Let y = tan ^-1 x

      x = tan y

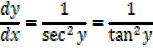
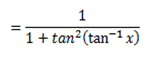
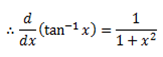
Let y =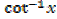

       X =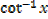

∴

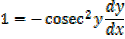
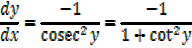
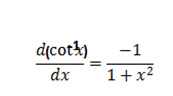
Exercises

        Differentiate the following with respect to x.

i)   Sin 6x

ii)   Cos (4x²+5)

iii)   Sec x tan ² x

        Differentiate sin2 (2x+4) with respect to x

        Differentiate the following from first principle

i)    Tan x

ii)  

Differentiation of logarithmic and exponential functions

1-     Let y = ln x

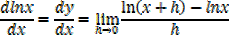
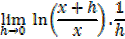
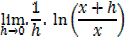
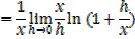
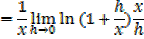
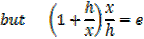
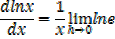
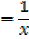
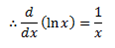
Example

Find the derivative of

Solution

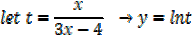
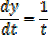
By quotient rule

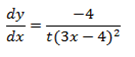
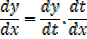
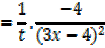
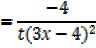
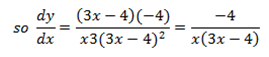
2-     Let y =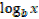

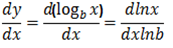
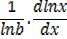
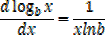
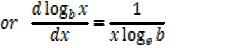
Differentiation of Exponents

1)     Let y = a^x

If a function is in exponential form apply natural logarithms on both sides

i.e.  ln y = ln a^x

ln y =x ln a

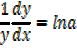
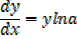
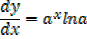
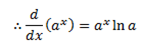
2)     Let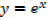

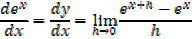
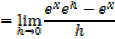
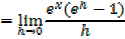
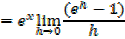
Since â”®^x does not depend on h,then

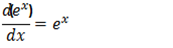
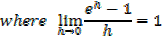
Therefore

Example

Find the derivative of y = 10^5x
Solution

Y = 10^5x

Iny = In10^5x

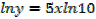
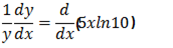
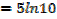
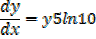
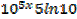
Therefore

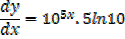
Exercise

Find the derivatives of the following functions

a)  a)   Y =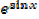

b)    b) Y =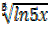

c)     c)Y=