ADVANCED MATHEMATICS FORM 5 – DIFFERENTIATION

APPLICATION OF DIFFERENTIATION

Differentiation is applied when finding the rates of change, tangent of a curve, maximum and minimum etc

i) The rate of change

Example

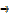The side of a cube is increasing at the rate of 6cm/s. find the rate of increase of the volume when the length of a side is 9cm

Solution

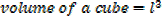
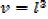
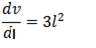
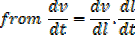
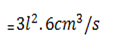
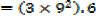
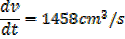
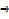A hollow right circular cone is held vertex down wards beneath a tap leaking at the rate of 2cm³/s. find the rate of rise of the water level when the depth is 6cm given that the height of the cone is 18cm and its radius is 12cm.

Solution

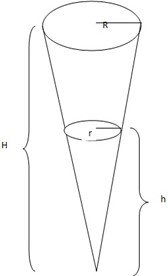
Volume of the cone

V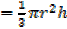

The ratio of corresponding sides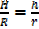

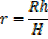
Given 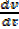= 20cm³/s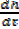

V=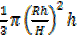

So ,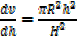

Then,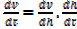

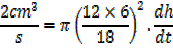
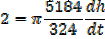
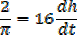
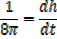
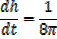
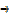A horse trough has triangular cross section of height 25cm and base 30cm and is 2m long. A horse is drinking steadily and when the water level is 5cm below the top is being lowered at the rate of 1cm/min find the rate of consumption in litres per minute

Solution

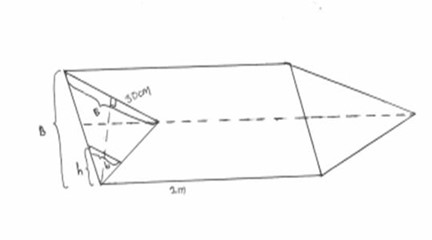
Volume of horse trough

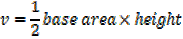
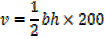
From the ratio of the corresponding sides

    

  

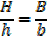
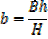
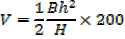
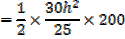
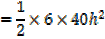
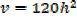
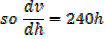
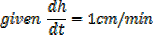
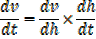
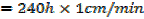
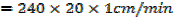
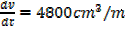
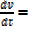
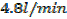
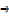A rectangle is twice as long as it is broad find the rate change of the perimeter when the width of the rectangle is 1m and its area is changing at the rate of 18cm²/s assuming the expansion is uniform

Solution

                                                                                                                                                                                                                 

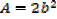
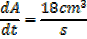
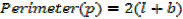
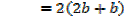
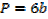
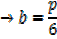
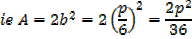
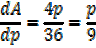
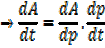
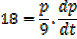
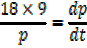
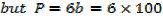
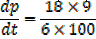
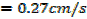
TANGENTS AND NORMALS

From a curve we can find the equations of the tangent and the normal

                        

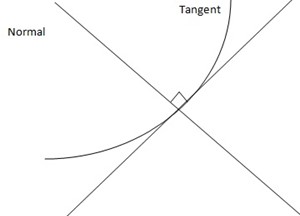
Example

        i.            Find the equations of the tangents to the curve  y =2x² +x-6 when x=3

Solution

 

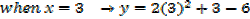
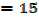
(x. y)= (3, 5) is the point of contact of the curve with the tangent

But

Gradient of the tangent at the curve is

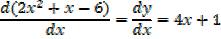
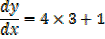
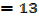
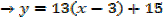
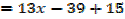
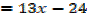
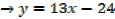
Example

     ii.            Find the equation of the tangent and normal to the curve y = x² – 3x + 2 at the point where it cuts y axis

Solution

The curve cuts y – axis when x = 0

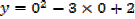
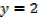
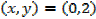
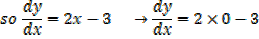
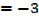
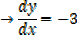
Slope of the tangent [m] = -3

Equation of the tangent at (0, 2) is

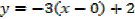
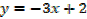
Slope of the normal

From; m₁m₂ = -1,Given m₁=-3

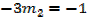
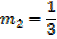
Equation of the normal is

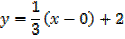
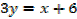
Exercise

  Find the equation of the tangent to 2x² – 3x which has a gradient of 1

  Find the equations of the normal  to the curve  y = x²-5x +6 at the points where the curve cuts the x axis

Stationary points [turning points]

A stationary point is the one where by 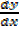 = 0 it involves:

        Minimum turning point

        Maximum turning point 

        Point of inflection                                                                                     

                                   

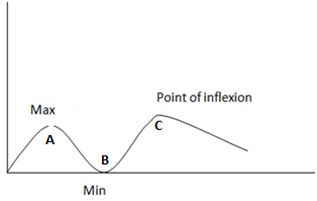
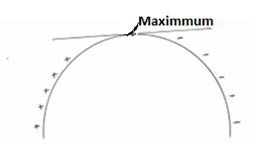
Nature of the curve of the function

At point A, a maximum value of a function occurs

At point B, a minimum value of a function occurs

At point C, a point of inflection occurs

At the point of inflection is a form of S bend

Note that

Points A, B and C are called turning points on the graph or stationary values of the function

Investigating the nature of the turning point

 Minimum points

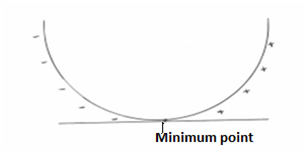
At turning points the gradient 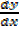  changes from being negative to positive i.e.

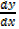 Increasing as x- increases

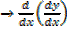 Is positive at the minimum point         

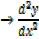  Is positive for minimum value of the function of (y)  

Maximum points

At maximum period the gradient changes from positive to negative

i.e.

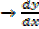   Decreases as x- increases

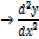 Is negative at the maximum value of the function (y)

Point of inflection 

This is the changes of the gradient from positive to positive

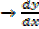 Is positive just to the left and just to the left

 

This is changes of the gradient from negative to negative.

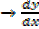 Is negative just to the left and just to the right

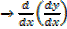   Is zero for a point of inflection i.e

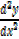     Is zero for point of inflection

Examples

Find the stationary points of the and state the nature of these points of the following functions

Y = x⁴ +4x³-6

Solution

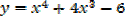
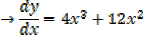
At stationary points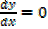

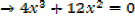
Therefore,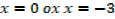

Then the value of a function

At x = 0, y = -6

X= -3, y =-33

Stationary point at (0,-6) and (-3,-33)

At (0,-6)

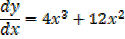
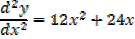
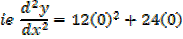
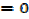
Point (0,-6) is a point of inflection

        At (-3,-33)

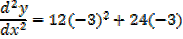
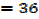
At (-3, -33) is a minimum point

Alternatively,

You test 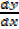   by taking values of x just to the right and left of the turning point

Exercise

1)     1. Find and classify the stationary points of the following curves

a)     (i) y = 2x-x²     

b)     (ii) y =  +x

c)     (iii) y= x²(x²– 8x)

2)    2. Determine the smallest positive value of x at which a point of inflection occurs on the graph of y = 3â”®^2x cos (2x-3)

3)    3. If 4x² + 8xy +9y² 8x – 24y +4 =0 show that when 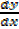= 0,

x + y = 1. Hence find the maximum and minimum values of y

Example

     1. A farmer has 100m of metal railing with which to form two adjacent sides of a rectangular enclosure, the other two sides being two existing walls of the yard meeting at right angles, what dimensions will give  the maximum possible area?

Solution       

                                            

Where, W is the width of the new wall

           L is the length of the new wall

The length of the metal railing is 100m

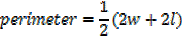
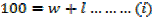
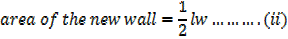
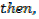
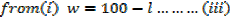
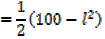
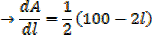
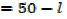
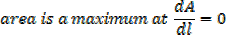
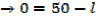
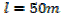
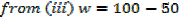
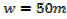
      2. An open  card board box width a square base is required to hold 108cm³ what should be the dimensions if the area of cardboard used is as small as possible

Solution

                 

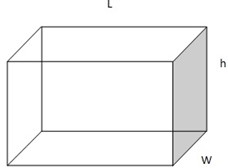
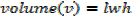
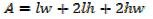
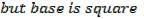
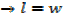
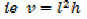
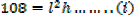
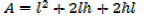
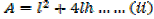
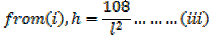
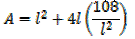
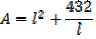
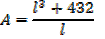
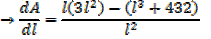
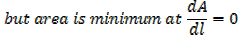
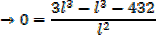
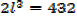
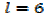
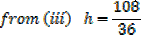
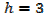
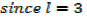
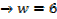
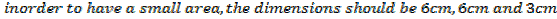
Exercise

The gradient function of y = ax² +bx +c is 4x+2. The function has a maximum value of 1, find the values of a, b, and c