ADVANCED MATHEMATICS FORM 5 – DIFFERENTIATION

MACLAURIN’S SERIES [from power series ]

Let f(x) = a₁ +a₂x+a₃x² +a₄x³ +a₅x⁴+ a₆x⁵…….i

In order to establish the series we have to find the values of the constant co efficient a₁, a₂, a₃, a₄, a₅, a₆ etc

Put x = 0 in …i

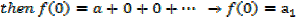
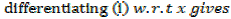
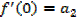
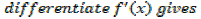
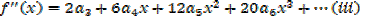
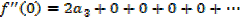
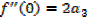
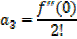
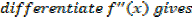
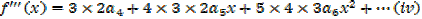
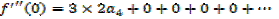
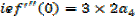
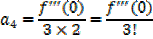
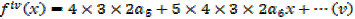
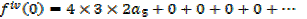
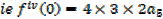
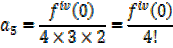
Putting the expressions a1,a2,a3,a4,a5,………back to the original series and get

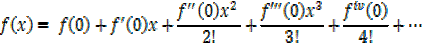which is the maclaurin series.

Examples

Expand the following

i)    â”®^x

ii)  f(x) = cos x

Solution

        i.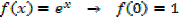     

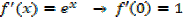
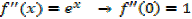
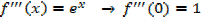
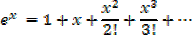
     ii.                       

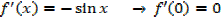
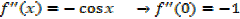
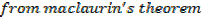
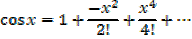
Exercise

        Write down the expansion of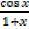                                 

        If x is so small that x³ and higher powers of x may be neglected, show that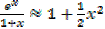

TAYLOR’S SERIES

Taylor’s series is an expansion useful for finding an approximation for f(x) when x is close to a

By expanding f(x) as a series of ascending powers of (x-a)

f(x) = a₀ +a₁(x-a) +a₂(x-a)²+a₃(x-a)³ +……..

This becomes

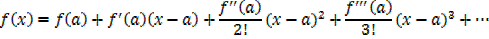
Example  

        Expand 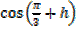in ascending powers of h up to the h³ term, taking as                

1.7321 And 5.5⁰ as 0.09599^c find the value of cos 54.5 to three decimal places

Solution

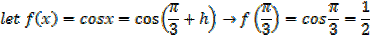
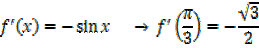
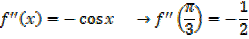
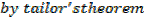
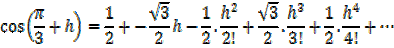
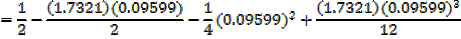
        Obtain the expansion of 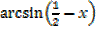in ascending powers of x as far as the x³term

Introduction to partial derivative

Let f (x, y) be a differentiable function of two variables. If y kept constant and differentiates f (assuming f is differentiable with respect to x)

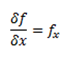
Keeping x constant and differentiate f with respect to y

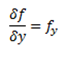
Example

        find the partial derivatives of f_x and f_y

If f(x, y) = x²y +2x+y

Solution

       

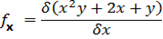
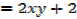
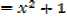
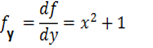
        Find f_x and f_y if f (x,y) is given by

f(x, y) = sin(xy) +cos x

Solution

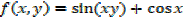
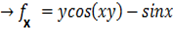
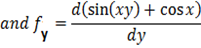
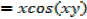
Exercise 

1.      find f_x and f_y if f(x,y) is given by 

a)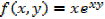    

b)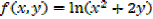    

c)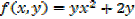    

d)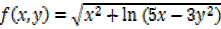    

     Suppose 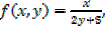 compute