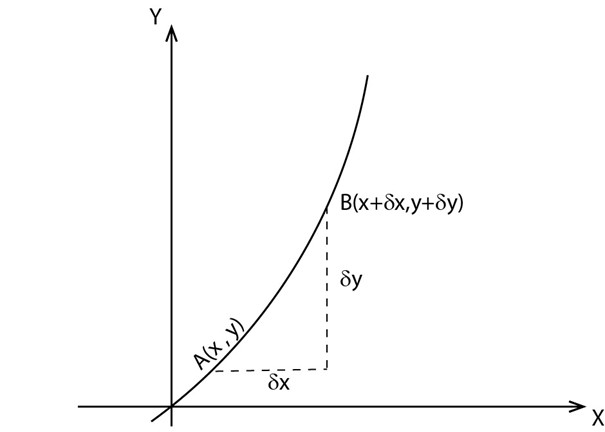
DIFFERENTIATION BY FIRST PRINCIPLE
Consider a curve that 
Let A(x, f(x)) be a point on the curve let B (x +  x, f ( x +
x, f ( x +  x )) be another point on the same curve
x )) be another point on the same curve
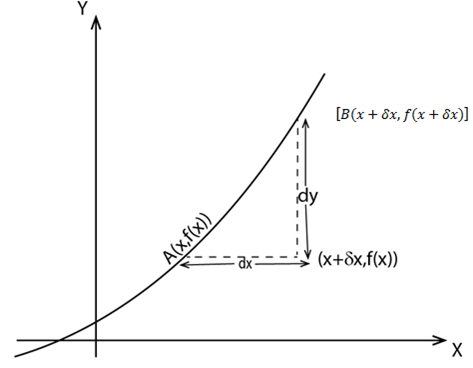
The gradient of AB
The gradient at A is given by
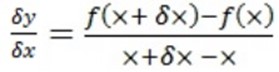
The gradient at A is given by;
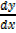 = limit
= limit 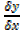
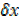
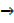 0
0
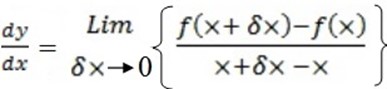
Examples
Differentiate the following using first principles
y = x2+3
y = x3+2x2+1
Solution
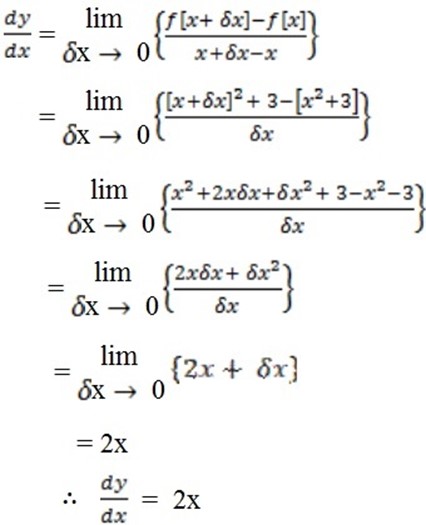
Solution
Exercise
1) y = x3-x2
2) y = 3x2-2x
3) y = 2x2-4x+1
4) y = 12x2-6x+7
5) y = x2+2x-2
Solutions
1) y = x3-x2
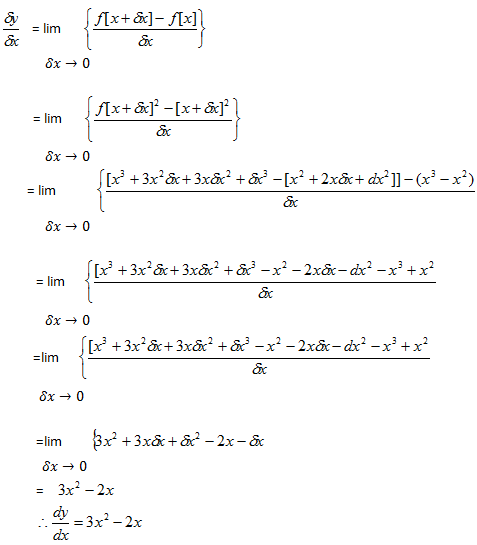
TECHNIQUES OF DIFFERENTIATION
A) DERIVATIVES OF POLYNOMIAL
1) Differentiation of constant [ i.e y = c]
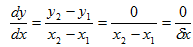
∴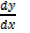 = 0
= 0
2) Differentiation of y = ax where a is a constant
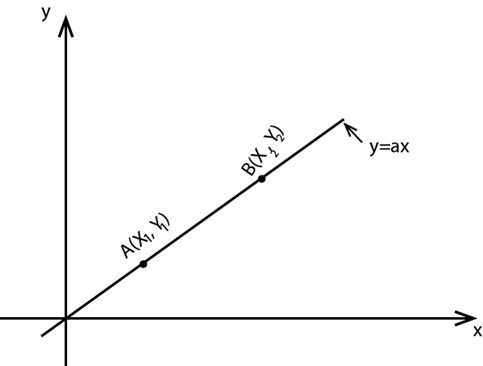
The gradient at B can be found by using the following
y = ax ………..(i)
Taking a point further
y + 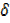 y = a(x +
y = a(x +  x)
x)
= ax + a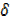 x ……..(ii)
x ……..(ii)
Subtracting y from (iii)
y + 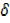 y –y = ax + a
y –y = ax + a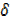 x – ax
x – ax
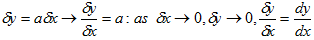
 =
= 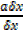
 = a
= a
3) Differentiation of y = x2
At point B
y + δy
y = [x+  x] 2
x] 2
= x2 + 2x 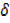 x+
x+ 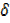 x2 …………… (i)
x2 …………… (i)
Subtract y from (i)
y2+ 2x x +
x +  x2 – x2= y +
x2 – x2= y + 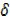 y – y
y – y
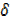 y = 2x
y = 2x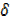 x+
x+ 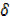 x2…….
x2…….
Dividing ….ii, by 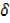 x …..
x …..
= 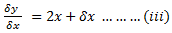
As 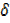 x
x 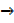 0,
0, 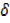 y
y 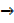 0,
0, 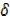 y /
y /  x = dy /dx
x = dy /dx
Equation becomes

Note
By proceeding with the same trend we shall get
When y = x4,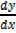 = 4x3
= 4x3
When y = x5, 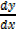 = 5x4
= 5x4
When y = x6, 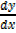 = 6x5
= 6x5
Generally
If y = xn , then
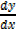 = nx n-1
= nx n-1
Example
Differentiate the following with respect to x.
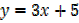
y = 6x7+5x4
y =-x10+9x2
Solution

Since differentiation of constant = 0
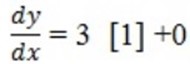
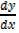 = 3+0
= 3+0
 = 3
= 3
y = 6x7+5x4-x2
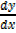 = 42x6+20x3-2x
= 42x6+20x3-2x
y =-x10+9x2
= 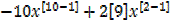
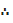
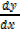 = -10x9+18x
= -10x9+18x
Exercise
Differentiate the following with respect to x.
i.) y =5x2+2
ii.) y =8x3-15x2+6x+2
iii.) y =x5-4x3
iv.) y = 6x2-x3+5x4
v.) y = 3x+10x2-4x7
Solution
y = 5x2 + 2
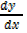 = 2[5] x[2-1] +2[0]
= 2[5] x[2-1] +2[0]
= 10x+0
= 10x
∴ = 10x
2.) y = 8x3-15x2+6x+2
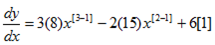
= 24x2– 30x + 6
3.) y = x5-4x3
 = 5x4-12x2
= 5x4-12x2
4.) y=6x2-x3+5x4
 =12x-3x2+20x3
=12x-3x2+20x3
DERIVATIVE BY USING CHAIN RULE
Is used to find derivative of function
Example:
Differentiate y = [3x+5]4
Solution
Let U = 3x+5
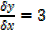
y =U4
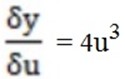
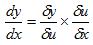
4u 3 x3
= 12u3
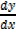 = 12 [3x+5]3
= 12 [3x+5]3
Note: This process is called chain rule
2) Find the 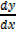 if y =
if y = 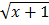
Solution
Let u = x+1
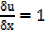
y = 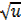
y = u ½
y = ½ u– ½
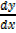 =
= 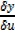 x
x 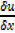
= ½ u– ½ x 1
= ½ [x+1]– ½