Differentiating by using product rule
Let y = uv where U and V are functions of x
If x 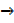 x +
x +  x, then U
x, then U 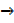 u +
u + 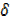 u
u
And V 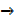 V +
V +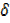 v
v
y 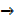 y +
y + 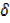 y
y
y + 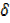 y = [u +
y = [u +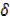 u] [v +
u] [v + 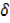 v]
v]
= uv + uδv + v 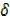 u +
u + 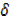 u
u 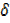 v …… i
v …… i
Subtracting y from …(.i)….
y + 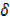 y –y = uv +uδv + vδu +
y –y = uv +uδv + vδu +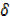 u
u 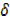 u – uv
u – uv
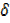 y = uδv+ v
y = uδv+ v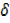 u +
u + 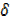 u
u 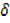 v ….(ii)
v ….(ii)
Dividing [ii] by 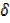 x
x
Exercise

Differentiating using quotient rule

then
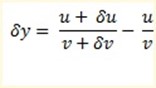
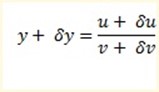

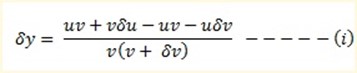
Divide by δx in equation (i) throughout.
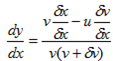
Taking the limits a
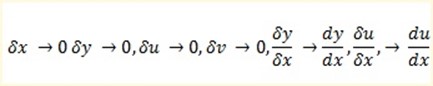

Then
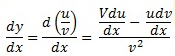
Exercise:Differentiate
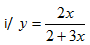
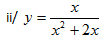
Solutions
y = x/cos x
Let u = x, v = cos x

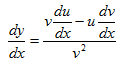
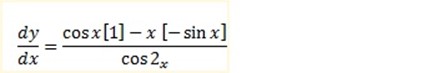
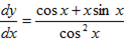
FIRST AND SECOND DERIVATIVES
The first derivative of the function
For example
If f [x] = x4
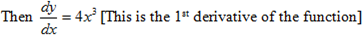
The second derivative is the derivative of the first derivative
For example
If f [x] = x4
Then
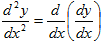
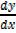 = [4x3]
= [4x3]
= 12x2
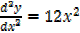
Examples
Find the second derivative of the following with respect to x
y = 2x5+ 4x3
y = x2+2x+1
Solution
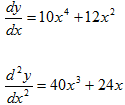
4.) y = x2 + 2x+1
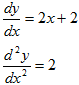
Note
d2y/dx2 may be represented by y” 0r f”(x).
Exercise
Find the derivative of the following
a.) f [ x] = x3+ 4x2-6x
b.) f [ x] = x2+3x
c.) f [ x] = 3x2+8x-6
d.) f [ x] = sin x
e.) f [ x] = cos x
Find f”(2) if
i.) f[ x] = x5+ 2x3-9x2+7x-1
ii.)
f[ x] = x4+5
iii.) f[ x] = x3 +4x2 – 6
Solution
1 a) f [x] = x3+4x2-6x
y = x3+4x2-6x

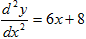
b) f [x] = x2 + 3x
y = x2 +3x
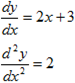
c) f [x] = 3x2+8x-6
y = 3x2+8x-6
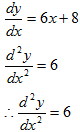
d) f [x] = sin x
y = sin x
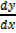 = cos x
= cos x
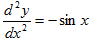
e) f [ x] = cos x
y = cos x
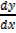 = -sin x
= -sin x
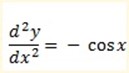
Solution
a) f [x] = x5+2x3-9x2+7x-1
y = x5+2x3-9x2+7x-1
f ‘[x] = 5x4+6x2-18x +7
f”[x] = 20x3+12x- 18
f”[2] = 20[2]3 + 12[ 2] -18
f “[2] = 160+24-18
f “[2] = 166
b) f [x] = x4+5
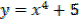
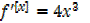
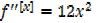
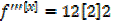 = 24x
= 24x
f “‘ (2) = 24(2)
f “‘(2) = 48
c) f(x) = x3 + 4x2 – 6
y = x3 + 4x2 – 6
Solution.
y’= 3x2 + 8x
y”(2)= 6x + 8
y”(2)= 6(2) + 8
y”(2)= 12+8
y”(2)=20
IMPLICIT DIFFERENTIATION
Consider the following functions
i) y = x2+4x+2
 y is an explicit function of x because it is considered completely in terms of x
y is an explicit function of x because it is considered completely in terms of x
ii) xy + sin y = 2
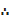 Y is an implicit function of x because it is implied in the function of x
Y is an implicit function of x because it is implied in the function of x
Example
1.) Find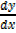 if x2y3 – xy = 10
if x2y3 – xy = 10
2.) Find 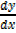 if y = sin x + cos y
if y = sin x + cos y
3.) Find 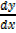 at [ -1,1] if x2 +3xy +y2 = 1
at [ -1,1] if x2 +3xy +y2 = 1
Solutions
1.) x2y3 – xy = 10
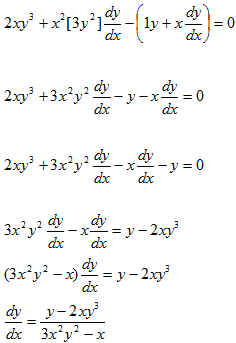
2.) y = sin x + cos y
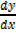 = cos x + [-sin y
= cos x + [-sin y 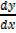 ]
]
 +sin
+sin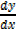 = cos x
= cos x
[1+ sin y] 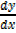 = cos x
= cos x
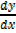 =
= 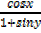
3.) x2 + 3xy +y2= 1
2x +3[ y + x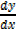 ] + 2y
] + 2y 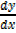 = 0
= 0
2x + 3y +3x 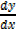 +2y
+2y 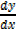 = 0
= 0
2x +3y + [3x + 2y] 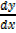 = 0
= 0
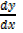 =
= 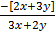
At [-1,1 ] 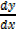 =
= 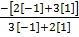
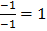
Exercise
Find dy/dx from the following equations
1) 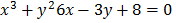
2) 
3) 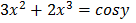
4) 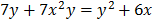
5) 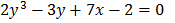
b) Rate of change
This is the change of one variable with respect to time
Examples
(1)The distances [meters] travelled by a body moving in a straight line in t [seconds] is given by S= 3t3-4t2
Find
The velocity after 2 seconds
The initial acceleration
(2)A 20m ladder leans a wall the top slides down at a rate of 4m/s . how fast is the bottom of the ladder moving when it is 16m from the wall
Solutions
If a 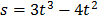
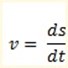
Differentiate [3t3-4t2]
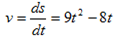
When t = 2, v = 9 x [ 2] – 8 [ 2]
v = [9 x 4] -16
v = 36-16
v = 20m /s
∴ The velocity after 2 seconds is
20m / s
a = 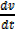
Initial acceleration is when t = 0
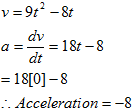
Solution
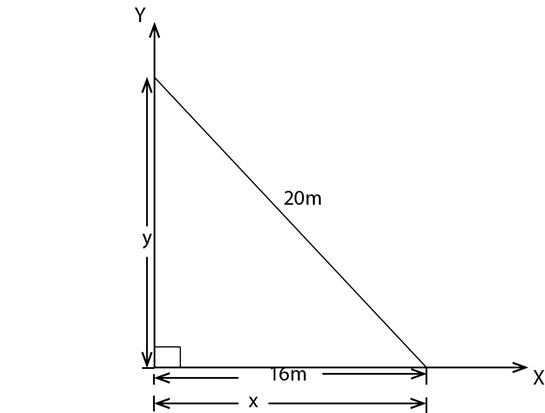
 ………….(i)
………….(i)
Differentiate [i] w.r.t ‘t’
2x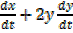 = 0
= 0
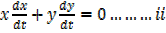
From [i]
y2 = 202-x2
y2 = [400] – [16]2
y2 = 400 – 256
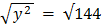
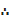 y = 12
y = 12
Substitute x and y in ii
16 dx /dt +12 dy /dt = 0

= 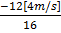
= 3 m /s
The bottom of the ladder is moving with the speed of 3m/s
Exercise
1.) The effectiveness of a pain killing drug t incurs after entering the blood stream is given by
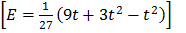
Find the rate of change of 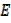 after
after
a.) 2 hours
b.) 3 hours
2.) A particle is moving in a straight line and its distance s in meters from a fixed point in the line after seconds is given by s = 12t – 15t2+4t3
Find
a.) the velocity of the particle after 3 seconds
b.) the acceleration of the particles after 3 seconds.
3.) When the height of a liquid in a container is h meters the volume of the liquid is v meters where v = 0.005 [3h +2]3-8
a.) Find the expression for dv/dh
b.) The liquid enters the container at of 0.08m3/s rate at which the height of the liquid is increasing when v = 0.95m3