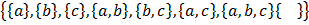The word set is used to denote a collection of well defined objects
Set are denoted by capital letters e.g. A, B, C, D etc
The statement ” x is an element of A” or ” x belong to A” is written as x ∈ A
If x is not an element of A, we write x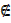 
A
Importance sets of the number system
IR: a set of real numbers (+, -) all numbers
IR+: Is a set of positive real numbers
IR–: Is a set of negative real numbers
Z: a set of integers. (+, -) whole numbers
Z+: a set of positive integers
Z–: a set of negative integers
Q: a set of rational numbers (rational ½ = 0.33333 – rational numbers, number repeats and terminate
N: a set of natural number (positive numbers starting from 1, 2, 3…… counting numbers)
SPECIFICATION OF A SET
There are two ways of specifying a set;
1. List its members (roster method)
2. Describing its elements by mathematical notation or actual words (builder notation).
Examples
1. Let A =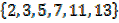 
specified in roster form, specify this by set builder notation
Solution
A is a set of all prime numbers less than 15
2. Let B =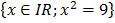 
specified by set builder, specify by roster form
Solution
Since x2 = 9, x = 3, x = -3
B =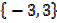 
The general form of set builder notation
A =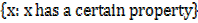 
OR
A =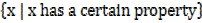 
E.g. A =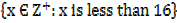 
QUESTIONS
1. Let A =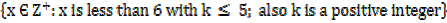 
a) Is 10 ∈ A NO
b) Is 11 ∈ A NO
c) Is 13 ∈ A NO
d) List all elements of A
A =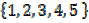 
2. Use the roster method to specify the following sets
a) A = {x ∈ Z: x + 3 = 5}
x + 3 = 5; x = 5 – 3, x = 2
A =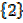 
b) B =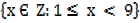 
B =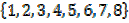 
c) C =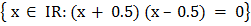 
x = -0.5 and x = 0.5
C=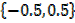 
3. Specify the following in roster form
a) A = {y ∈ Z: y= 3K where K∈Z+ and K ≤ 6}
Solution
K =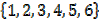 
Y =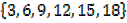 
A =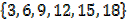 
b) B =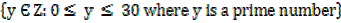 
y =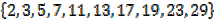 
B =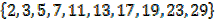 
BASIC CONCEPTS OF SET.
1. The set that does not contain any element is called an empty set, donated by Φ or { }
2. Universal set is a set which contains all elements under consideration. It is denoted by µ.
3. Equality; two sets are equal if they have same elements
i.e. If A =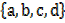 
and B =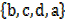
4. Equivalent; two sets are equivalent if they have same number of elements
i. e A =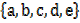
and B = 
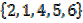∴A≡B
5. Subsets; A is a subset of B if every member of A is also a member of B. It is denoted by A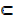
B
6. Improper subset; suppose A =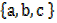 
and B =
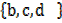A
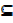B
7. Proper subset. Suppose A =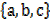 
and B = 
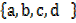A
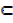B
Note i)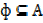 
(an empty set is subset of any set)
ii) A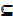
A (a set is subset of its own set)
Number of subsets in a set
Let S =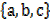 
How many subsets does it have?
The subsets are: { }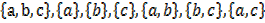 
→There are 8 subsets of S.
If A =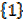 
and If B =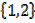 
Subset of A are :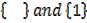 
Subsets of B are :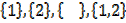 
Number of subsets of A= 2 Number of subset of B = 4
If a set has n members, the number of subsets = 2n
THE POWER SET
Is a set which contains all subsets of the given sets
If A =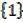
, subsets are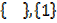 
Power set of A is given by S =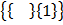 
Given B =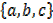 
The power set of B is given by
S = 