OPERATION OF SETS
1. UNION
The union of two sets A and B is denoted by AUB
– AUB = 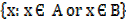
– Is a set which have elements of set A or set B without repetition.
Examples
→If A =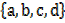 and B =
and B = 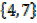
AUB = 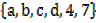
→If A =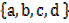 and B =
and B = 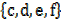
AUB = 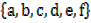
2. INTERSECTION
– Is a set which have both elements contained in set A and set B
A∩B = {x:x∈A and x∈B}
Examples
→If A = 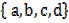 and B =
and B =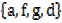
A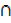 B =
B =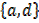
→If A =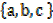 and B =
and B = 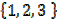
A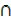 B =
B = 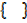
Here A and B are disjoint sets.
3. COMPLEMENT
The complement of Set A denoted by A′ is the set of all elements which are in universal set but not in A.
E.g. A =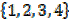
µ= 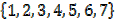
A′ = 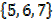
4. RELATIVE COMPLEMENT
Relative complement of A with respect to set B is denoted by A’ B or A – B and is defined as follows
A B =
B =
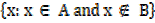
Example
A = 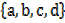
B = 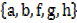
Then A B =
B = 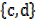
B A =
A = 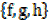
5. THE SYMMETRIC DIFFERENCE
All elements which are either in set A or set B but not both
– The symmetric difference of A and B is denoted by A 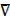 B
B
A 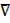 B =
B = 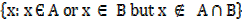
Examples
A = 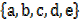
B = 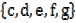
A 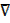 B =
B = 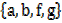
QUESTIONS
1. List the subsets of the following sets
a) A = 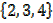
b) B = 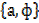
2. Let A = 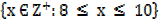
Write down the subsets of A
3. Which of the following are true and which are false?
a) Φ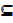 Φ b) 0 = Φ c) Φ∈
Φ b) 0 = Φ c) Φ∈
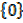 d) Φ ∈
d) Φ ∈
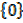
4 . Let A = 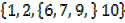
a) Is 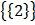 ∈ A
∈ A
b) Is 2 ∈ A
c) Is 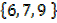 ∈ A
∈ A
d) Is 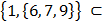 A
A
e) Is 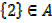
f) Is 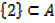
5. Let µ be the set of all positive integers, A is the set of all even integers and B is a set of all odd integers. What are sets?
a) A 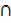 B b) A
B b) A 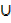 B c) A
B c) A 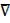 B d) A’ e) B’ f) A
B d) A’ e) B’ f) A B
B
QUESTIONS
1. Let µ be the universal set and Φ be an empty set. What are
a) Φ = µ
b) µ = Φ
c) µ – Φ = µ
d) Φ – µ = Φ
e) µ ∩ Φ = Φ
f) µ 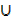 Φ = µ
Φ = µ
2. Let A be subset of the universal set µ. What are the following?
a) A 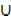 Φ = A
Φ = A
b) A 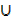 A = A
A = A
c) A 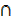 Φ = Φ
Φ = Φ
d) A 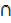 A = A
A = A
e) A 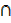 µ = A
µ = A
f) A 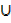 µ = µ
µ = µ
g) A ∩ A’ = Φ or {}
h) A 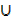 A‘= µ
A‘= µ
i) A 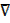 µ = A‘
µ = A‘
j) A 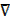 Φ = A
Φ = A
3. Let A and B be subsets of a universal set µ. Suppose A 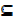 B. What are;
B. What are;
a) A U B = B
b) A  B = A
B = A