SET INTERVAL ON THE NUMBER LINE
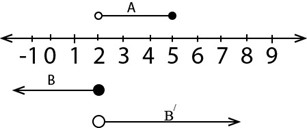
1. Let A = 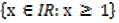 and B={x∈IR:-7< x ≤ 3}Represents these set intervals on two separate number lines
and B={x∈IR:-7< x ≤ 3}Represents these set intervals on two separate number lines
Solutions
For A = 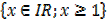

For B = 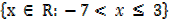

Examples
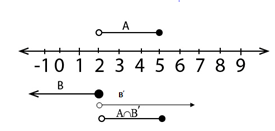
Using the sets A and B defined above, state and represents the following sets on same number line
a) A 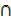 B b) A′ c) B′ d) A U B′
B b) A′ c) B′ d) A U B′
Solutions
a) A  B
B
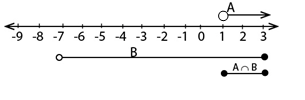
A 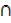 B =
B = 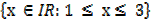
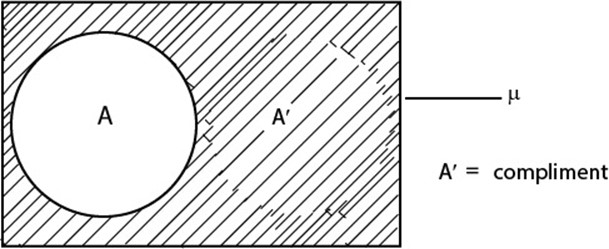
b) A′
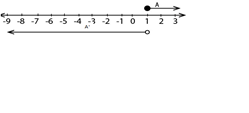
A′ = 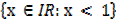
c)B′

B′ = 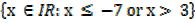
a)
(d)A U B′
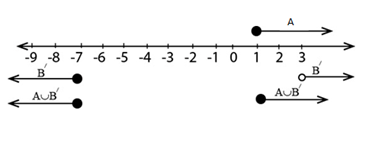
A U B′ =
QUESTION
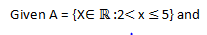
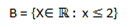
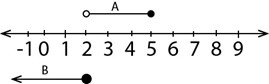
i) Represent the above sets on one number line
ii) Draw and state each of the following sets on separate number lines
a) A ∩ B b) A ∪B c) B′ d) A∩B′
Solution
(i)
(ii)(a) A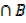

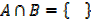
b) A U B


c) B′
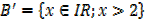

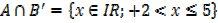
QUESTIONS.
1. Represents and then draw on one number line the following set interval
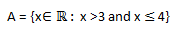
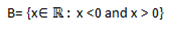
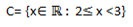
Using the above set interval, represent and state the following
i) A  B ii) A
B ii) A 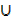 C iii) C
C iii) C 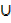 B‘ iv) (A
B‘ iv) (A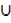 B)
B) 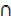 C
C
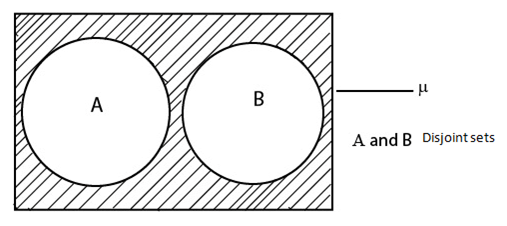
VENN DIAGRAMS
Sets can be represented in the form of diagrams called Venn diagrams
– The universal set is represented by a rectangle
– Subsets of U are represented by a circle in universal set
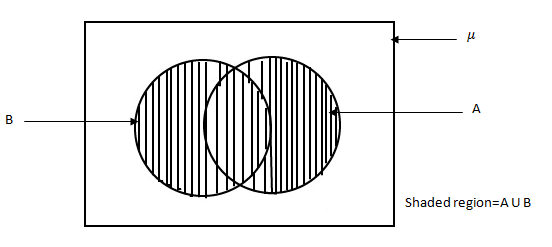
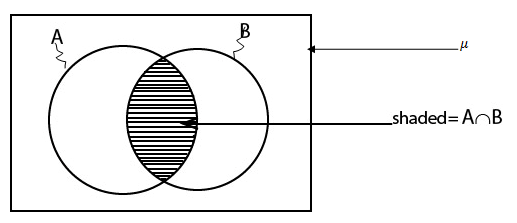
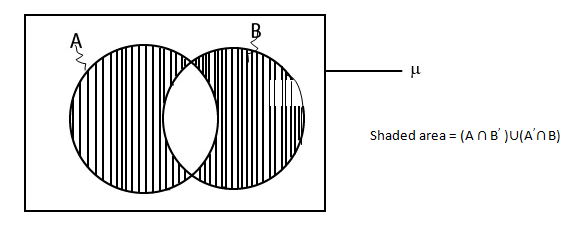
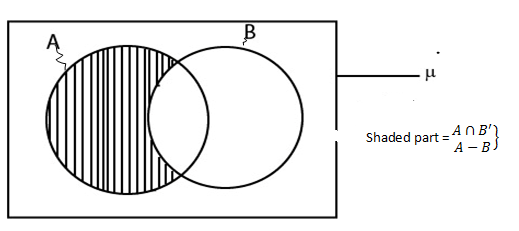
Uses of Venn diagram
i) To illustrate sets identity
ii) To find number of members in a given set
1. Illustration of set identity
Example; Illustrate by use of Venn diagram (A U B)  A = A
A = A
Solution.
Two different methods can be used
i) Shading method
ii) Numbering of disjoint subsets
i) Shading method, i.e. to show (A  B) ∩ A = A
B) ∩ A = A
L. H. S → (A 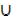 B) ∩ A
B) ∩ A
Shade (A 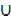 B) by vertical lines
B) by vertical lines
Shade (A 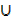 B)
B) 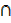 A by horizontal lines
A by horizontal lines
Now (A  B)
B)  A = region shaded
A = region shaded
= A
= R. H. S
∴ (A 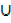 B)
B) 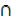 A = A
A = A
ii) Numbering of disjoint
Solutions
L. H. S = (A 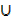 B)
B)  A
A
Now A 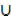 B = subsets 1, 2, 3
B = subsets 1, 2, 3
But A = sub 1, 2
(A  B)
B)  A = subsets 1, 2
A = subsets 1, 2
=A
= R. H. S
Example
Use Venn diagram to show A (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C)
C)
Solution
L. H. S = A U (B  C)
C)
Now B  C
C  subsets 5, 6
subsets 5, 6
A U (B 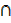 C)
C) Subsets 1, 2, 5, 4 and 6
Subsets 1, 2, 5, 4 and 6
R. H. S = (A U B) 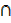 (A U C)
(A U C)
A U B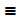 subsets 1, 2, 3, 4, 5, 6
subsets 1, 2, 3, 4, 5, 6
A U C 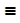 subsets 1, 2, 3, 4, 5, 6, 7
subsets 1, 2, 3, 4, 5, 6, 7
(A U B) ∩ (A U C) = 1, 2, 5, 4, 6
A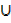 (B
(B 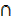 C) = (A
C) = (A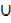 B)
B) 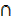 (A
(A 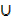 C)
C)
QUESTION
Use a Venn diagram to show the following
i) (A  B)
B) 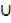 A = A
A = A
ii) A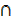 (B
(B 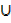 C) = (A
C) = (A  B)
B) 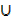 (A
(A 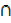 C)
C)
LAWS OF ALGEBRA OF SETS
Set operations obey the following laws
1. Commutative laws
A U B = B U A
A 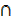 B = B
B = B 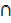 A
A
2. Associative laws
a) (A U B) U C = A U (B U C)
b) (A 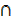 B)
B) 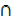 C = A
C = A 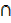 (B
(B 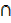 C)
C)
3. Distributive laws
a) A U (B 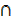 C) = (A U B)
C) = (A U B)  (A U C)
(A U C)
b) A 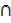 (B U C) = (A
(B U C) = (A 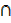 B)
B) 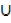 (A
(A 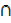 C)
C)
4. De -Morgan’s laws
a) (A U B)′ = A′ 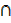 B′
B′
b) (A 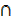 B)′ = A′U B′
B)′ = A′U B′
5. Identity laws
a) A 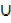 µ = µ
µ = µ
b) A 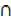 µ = A
µ = A
c) A 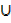 Φ = A
Φ = A
d) A 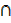 Φ =Φ
Φ =Φ
e) A\Φ = A
f) A\A = Φ
Examples
Use laws of algebra of set to simplify
1. (A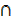 (A
(A 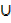 B)′)′
B)′)′
Solution
(A 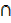 (A
(A  B)′)′ ≡(A
B)′)′ ≡(A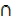 (A′
(A′ 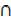 B′))′ De-Morgan’s law
B′))′ De-Morgan’s law
≡((A 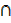 A′)
A′) B′ )′Associative law
B′ )′Associative law
≡ (Φ 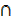 B′) Complement law
B′) Complement law
≡ (Φ)′Identity law
≡ µ complement law
 (A
(A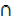 (A U B)′)′ = µ
(A U B)′)′ = µ
Examples
Use the laws of algebra of sets to prove
(A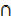 (B
(B 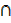 C′))
C′)) 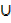 C = (A
C = (A 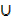 C)
C) 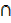 (B
(B 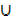 C)
C)
Solution
L.H.S (A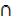 (B
(B 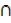 C′))
C′)) 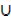 C
C
= (((A 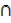 B) C′)
B) C′)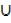 C…….. Associative law
C…….. Associative law
=((A 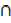 B) U C)
B) U C) 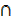 (C′
(C′ 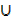 C) ………distributive law
C) ………distributive law
= ((A  B)
B) 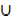 C)
C) 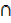 (µ) …………complement law
(µ) …………complement law
= (A 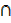 B)
B) 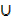 C……………. identity law
C……………. identity law
= (A 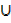 C)
C) 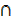 (B
(B  C) ……………distributive law
C) ……………distributive law
= R. H. S
Exercise
1. Use laws of algebra of set to simply
i) (A  B)
B)  (A
(A  B’)
B’)
ii) (A’  B’)
B’) 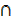 (A
(A 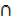 B)
B)
iii) (A 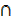 B) U (A – B)
B) U (A – B)
iv) A 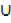 (A
(A 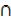 B)
B)
2. Use laws of algebra to prove
i) (Z 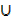 W)′
W)′ 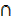 W = Φ
W = Φ
ii) (X 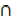 Y’)
Y’) 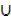 (X
(X 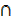 Y)
Y)  (Y
(Y 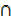 X′) = X
X′) = X  Y
Y
iii) (A – B) 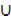 A = A
A = A
Note
A – B = A  B′ by definition
B′ by definition
Number of elements in a set
The number of elements in set A is denoted by n (A)
Example
Let A be a set of all positive odd integers which are less than 10. Find n (A)
Solution
A = {1, 3, 5, 7, 9}
Now n (A) = 5
Examples
Let A ={x ∈ IR:x2-x-2=0}. Find n (A)
Solution

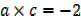
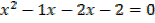
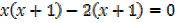

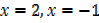
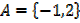
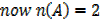
Note
i) The number of elements of a set is defined only for a finite set
ii) If A  U then the number of elements of A′ is n(A′) = n(µ) – n(A)
U then the number of elements of A′ is n(A′) = n(µ) – n(A)
Example
If A 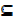 U and B
U and B 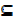 U then show that n (A
U then show that n (A 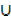 B) = n(A) + n(B) – n(A
B) = n(A) + n(B) – n(A 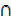 B)
B)
Proof
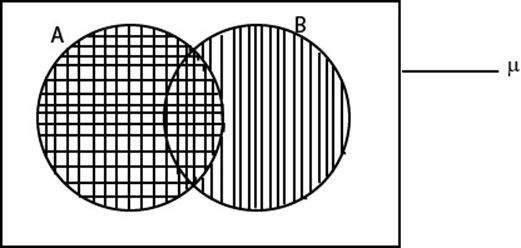
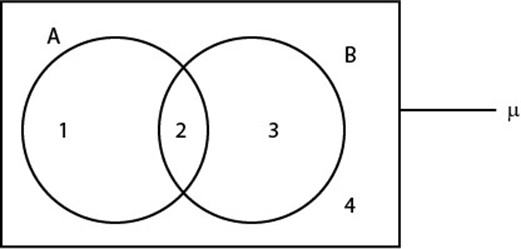
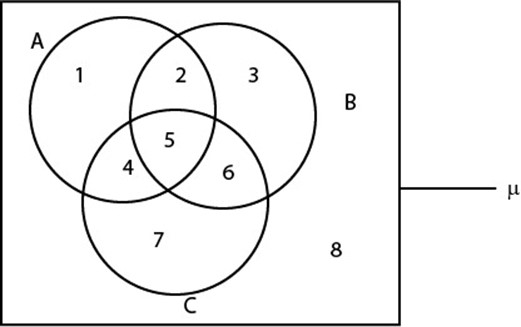
Refer to the Venn diagram below
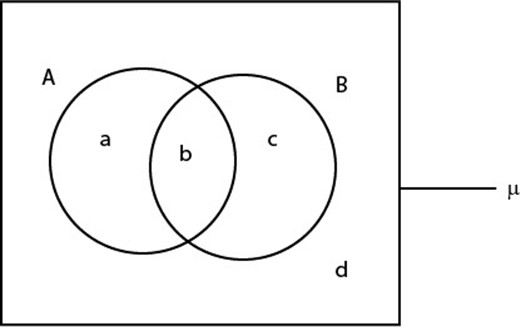
Represents the number of elements in disjoint subset as follows
Let n (A  B′) = a n (A′
B′) = a n (A′  B) = c
B) = c
n (A 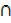 B) = b
B) = b
R. H. S = n (A) + n (B) – n (A 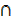 B)
B)
= (a + b) + (b + c) – b
= a + 2b + c – b
= a + b + c
n (A 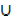 B)
B)
L. H. S