EXAMPLE
1. Given n (X) = 18, n (Y) = 26, n (X ∩ Y) = 12. Find n (X 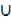 Y)
Y)
2. Given n (S 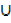 T) = 19, n (s) = 15. n (S
T) = 19, n (s) = 15. n (S 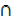 T′) = 10. Find n(S
T′) = 10. Find n(S 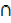 T)
T)
3. Given n (A 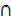 B) = 15
B) = 15
n (A 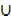 B) = 16
B) = 16
n ((A  B)′) = 4
B)′) = 4
n (A – B) = 8
Find i) n (A) ii) n (A 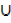 B′) iii) n (µ) iv) n (A′
B′) iii) n (µ) iv) n (A′ 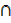 B)
B)
Solutions
1. n (X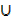 Y) = n (X) + n (Y) – n (X
Y) = n (X) + n (Y) – n (X Y)
Y)
=18 + 26 – 12
= 32
n (X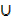 Y) = 32
Y) = 32
2. n(S  T) = 19, n(S) = 15, n(S
T) = 19, n(S) = 15, n(S 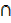 T’) = 10
T’) = 10
i) n(S 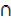 T) =?
T) =?
n(S 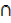 T) = n(S) – n(S
T) = n(S) – n(S 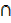 T’)
T’)
= 15 – 10
= 5
n( S 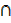 T) = 5
T) = 5
3. n(A 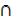 B) = 5, n(A
B) = 5, n(A  B) = 16, n(A
B) = 16, n(A 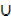 B)′ = 4, n(A – B) = 8
B)′ = 4, n(A – B) = 8
i) n(A) =? ii) n (A 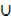 B′) iii) n(µ) iv) n (A′
B′) iii) n(µ) iv) n (A′ B)
B)
Solutions
n (A) = n(A – B) + n(A  B)
B)
= 8 + 5
= 13
ii) n (A 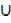 B’) = n (A) + n(B′)
B’) = n (A) + n(B′)
= 13 + 4
= 17
n(A 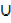 B’) = 17
B’) = 17
iii) n(µ) = n(A 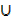 B) + n(( A
B) + n(( A 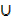 B))′
B))′
= 16 + 4
= 20
n(µ) = 20
iv) n(A′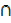 B) = n(B) – n(A
B) = n(B) – n(A 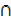 B)
B)
n(A′ 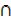 B) = n(A
B) = n(A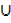 B) – n(A) + n(A
B) – n(A) + n(A 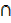 B) – n (n (A
B) – n (n (A 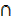 B))
B))
n(A′  B) = 16 – 13
B) = 16 – 13
n (A′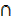 B) = 3
B) = 3
4. By using n (A 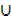 B) = n(A) + n(B) – n(A
B) = n(A) + n(B) – n(A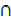 B) show that;
B) show that;
n(A 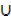 B
B 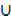 C) = n(A) + n(B) + n(C) – n(A
C) = n(A) + n(B) + n(C) – n(A 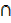 B) – n(A
B) – n(A  C) – n(B
C) – n(B 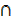 C) + n(A
C) + n(A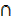 B
B 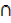 C)
C)
Solutions
Let B  C = K
C = K
L.H.S n(A 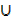 B
B 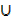 C) = n(A
C) = n(A 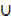 K)
K)
= n(A) + n(K) – n(A 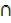 K)
K)
= n(A) + n(B 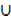 C) – n(A
C) – n(A 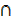 (B
(B 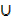 C))
C))
= n(A) + n(B) + n(C) – n(B 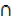 C) – n((A
C) – n((A 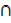 B)
B) 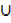 (A
(A  C))
C))
= n(A) + n(B) + n(C) – n(B 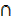 C) – (n(A
C) – (n(A  B) + n( A
B) + n( A 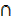 C) – n((A
C) – n((A 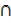 B)
B)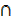 (A
(A 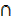 C))
C))
= n(A) + n(B) + n(C) – n(B 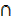 C) – n(A
C) – n(A 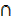 B) – n(A
B) – n(A 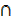 C) + n(A
C) + n(A 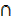 B
B 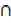 C)
C)
Questions
There are 26 animals in zoo, 5 animals eat all type of food in the zoo i.e. grass, meat and bones. 6 animals eat grass and meat only, 2 animals eat grass and bones only, 4 animals eat meat and bones only. The number of animals eating one type of food only is divided equally between the three types of food.
i) Illustrate the above information by a labeled Venn diagram
ii) Find the number of animals eating grass
Solutions
Let M  set of animals that eat meat
set of animals that eat meat
Let B  set of animals that eat bones
set of animals that eat bones
Let G  set of animals that eat grass
set of animals that eat grass
3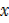 + 6 + 5 + 4 + 2 = 26
+ 6 + 5 + 4 + 2 = 26
3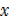 + 17 = 26
+ 17 = 26
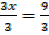
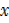 = 3
= 3
ii) Number of animals eating grass
= 6 + 5 + 2 + 3
= 16 animals
Questions
1. A class has 15 boys and 15 girls. In the class 20 students are studying science, 14 students are studying math, 10 boys are studying science, 10 boys are studying math, 8 boys are studying both math and science, 4 girls are studying neither math nor science.
Find i) How many students study math only?
ii) How many students study science only?
iii) How many students study both math and science?
2. In a class of 35 students each students each student takes either one of two subjects (physics, chemistry and biology). If 13 students take chemistry, 22 students take physics,17 students take biology, 6 students take both physics and chemistry and 3 students take both biology and chemistry. Find the number of students who take both biology and physics.
Solutions
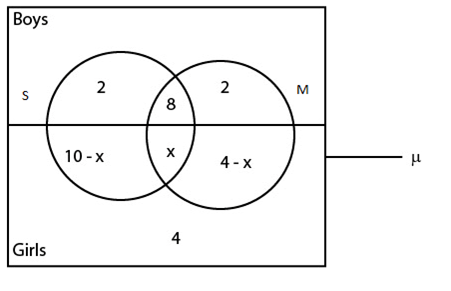
Since there are 15 girls
10 – 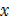 +
+ 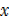 + 4 –
+ 4 – 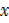 + 4 = 15
+ 4 = 15
18 – 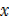 = 15
= 15
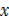 = 3
= 3
i) Students who study math only = 2 + 1
= 3 students
ii) Students who study science only = 2 + 7
= 9 students
iii) Students who study both math and science = 8 + 3
= 11 students
QUESTIONS
1. In a certain college apart from other discipline, no students is allowed to study less than two of the subjects, finance, accounting and economics, 150 students study finance, 110 study accounting, 80 study economics and 20 study three subjects
i) How many students study two of the named subjects?
ii) How many study finance or accounting or economic?
2. One poultry farm in Dar produces three types of chicks and in six months report revealed that out of 126 of its regular customers, 65 bought broilers, 80 bought layers and 75 bought cocks, 45 bought layers and cocks, 35 bought broilers and cocks, 10 bought broilers only, 15 bought layers only and bought cocks only, 6 of the customers did not show up.
i) How many customers bought all the three products?
ii) How many customers bought exactly two of the products?
3. An investigator was paid sh. 100 per person interviewed about their likes and dislikes on a drink for lunch. He reported 252 responded positively coffee, 210 liked tea, 300 liked soda, 80 liked tea and soda, 60 liked coffee and soda. 50 liked all three, while 120 people said they not like any drink at all. How much should the investigator be paid coffee and tea 60 people?