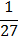BAM FORM 6 – EXPONENTIAL AND LOGARITHMIC FUNCTIONS

BASIC PROPERTIES OF EXPONENTIAL FUNCTIONS

If a is a real number and a is greater than 0 (a>0) then;

F(x) =  is called an exponential function

Examples:

1.      f (x) =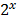 

2.      f (x) =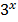  

3.      f (x) =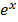 

4.      f(x)=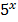

Graphs of Exponential Function:

Example:

Draw the graph of f(x) =

Solution:

The properties of exponential functions

-Any Function of the form f (x) = 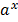 has the following properties

                                         i.   Increases when x is (+ve)

                                         ii.   Decrease when x is (-ve)

                                         iii.  It is constant when x=1

                                         iv.   It’s graph passes through (0,1)

                                         v.   It is one-to-one function

                                         vi.  It’s domain is {x: x∈IR}

                                        vii.   It’s range is {y: y is positively}

                                        viii.  It’s horizontal asymptotes at y=0

     Roles of Exponential Functions

1.     If n 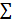N then  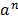is the  product of N

This means;

If 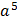= a x a x a x a x a

But 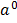=1

2.      If n,m 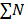, then

            i.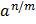=  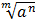= ( 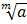)ⁿ

           ii^. =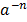

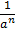
           iii.  =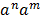

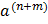
           iv. =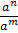

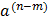
           V. (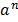) ^m =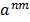

Example

Solve 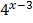 = 8

Express them in terms of base 2

      =

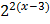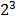
    2(x-3) = 3

    2x-6=3

    2x = 3 + 6

        =

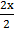     X = 4.5

EXERCISE

1.      Draw graphs of the following functions and determine the domain and range.

a)f(x) =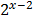  

b)  f(x) = 2 +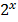  

c)   f (x) =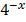

2.      Solve for x

a) 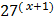  = 9 

b)   =  

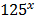
           c)    =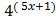

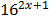
d)    =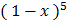  

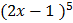
           e)  =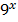

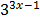
THE CALCULUS OF EXPONENTIAL FUNCTIONS

         A)   The derivative of  f (x) =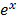

     Recalling that:

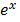       = 1 + x +  +  +  + …………

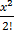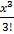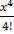      If y =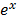

       =  ()

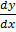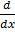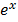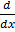  =  (1 + x +  +  +  + …………

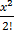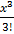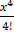  = 0 + 1 +  +  +  + …….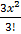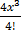