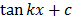BASIC PROPERTIES OF LOGARITHMIC FUNCTIONS
If a is any positive real number which in not equal to 1, then a function f (x) defined as f (x) = 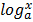 for x> 0 is called a logarithmic function.
for x> 0 is called a logarithmic function.
Examples:
i. 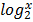
ii. 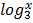
iii. 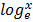
iv. 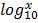
Graphs of logarithmic functions
Draw graph of f (x) = 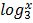
Solution
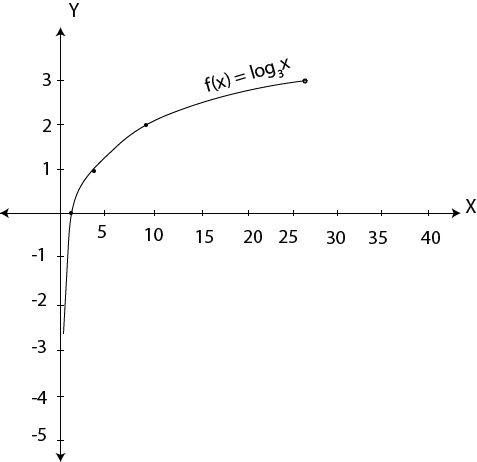
Properties of logarithmic functions
i. It’s graph passes through (1,0)
ii. It’s domain is ( x : x > 0)
iii.It’s range is (y:y∑IR)
iv.It’s a one to one function
v. It is the inverse of exponential function
vi.It’s vertical asymptote is at x = 0
vii.No horizontal asymptote
LAWS OF LOGARITHMS:
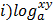 =
= 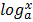 +
+ 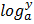
ii).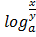 =
=  –
– 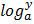
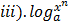 = n
= n 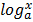
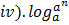 = n
= n
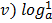 = 0
= 0
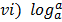 = 1
= 1
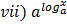 =x , x > 0
=x , x > 0
CHANGING BASES OF LOGARITHM
Let y = 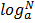
Change it into base b
Steps:
i. Express logarithmic function into exponential function
Y = 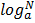 …………. (i)
…………. (i)
N = 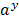 ……………. (ii)
……………. (ii)
Introduce logarithm to base b both sides:
N = 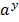
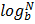 =
= 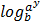
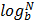 = y
= y 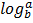 ………….. (iii)
………….. (iii)
Divide (iii) by 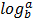 ………… (iii)
………… (iii)
 y =
y = 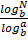
Examples
Evaluate the following to four decimal places
1. 
2. 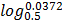
Solution
1. 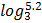
Let y = 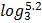
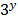 = 5.2
= 5.2
Introducing natural logarithm
In 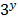 = In 5.2
= In 5.2
yln 3 = in 5.2
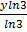 =
= 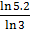 =
= 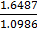
 y = 1.5007
y = 1.5007
2. 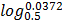
Let y = 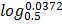
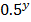 = 0.0372
= 0.0372
In 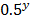 = ln 0.0372
= ln 0.0372
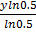 =
= 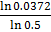 =
= 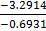
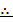 y = 4.7488
y = 4.7488
EXERCISE
1. Evaluate the following correct to 4 decimal places
a) Log 49236
b) Ln 54.02
c) 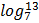
d) 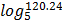
e) 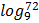
f) 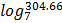
2. Change to base e
a) Log 5.3147
b) Log 0.053
3. Change to base 10
a) ln2.0103
b) ln 47.486
4. Draw graphs of
a) f (x) = 
b) f (x) = 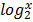
INTEGRATION OF TRIGONOMETRIC FUNCTIONS
a) Integration of sin x
Recalling;
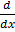 (
(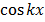 ) = -k
) = -k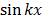
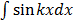 =
= 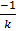
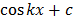
Example
Compute
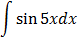
Solution
Let u = 5x
Du = 5dx
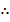 dx =
dx = 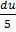
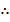
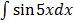 =
= 

= 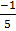
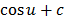
=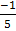
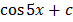
b) Integration of 
Recalling

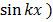 = k
= k 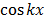
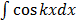 =
= 
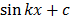
c) Integration of sec2x
Recalling
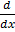
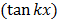 = k sec2kx
= k sec2kx
 ʃsec2kxdx =
ʃsec2kxdx =